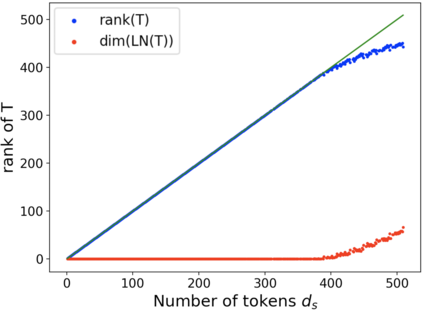
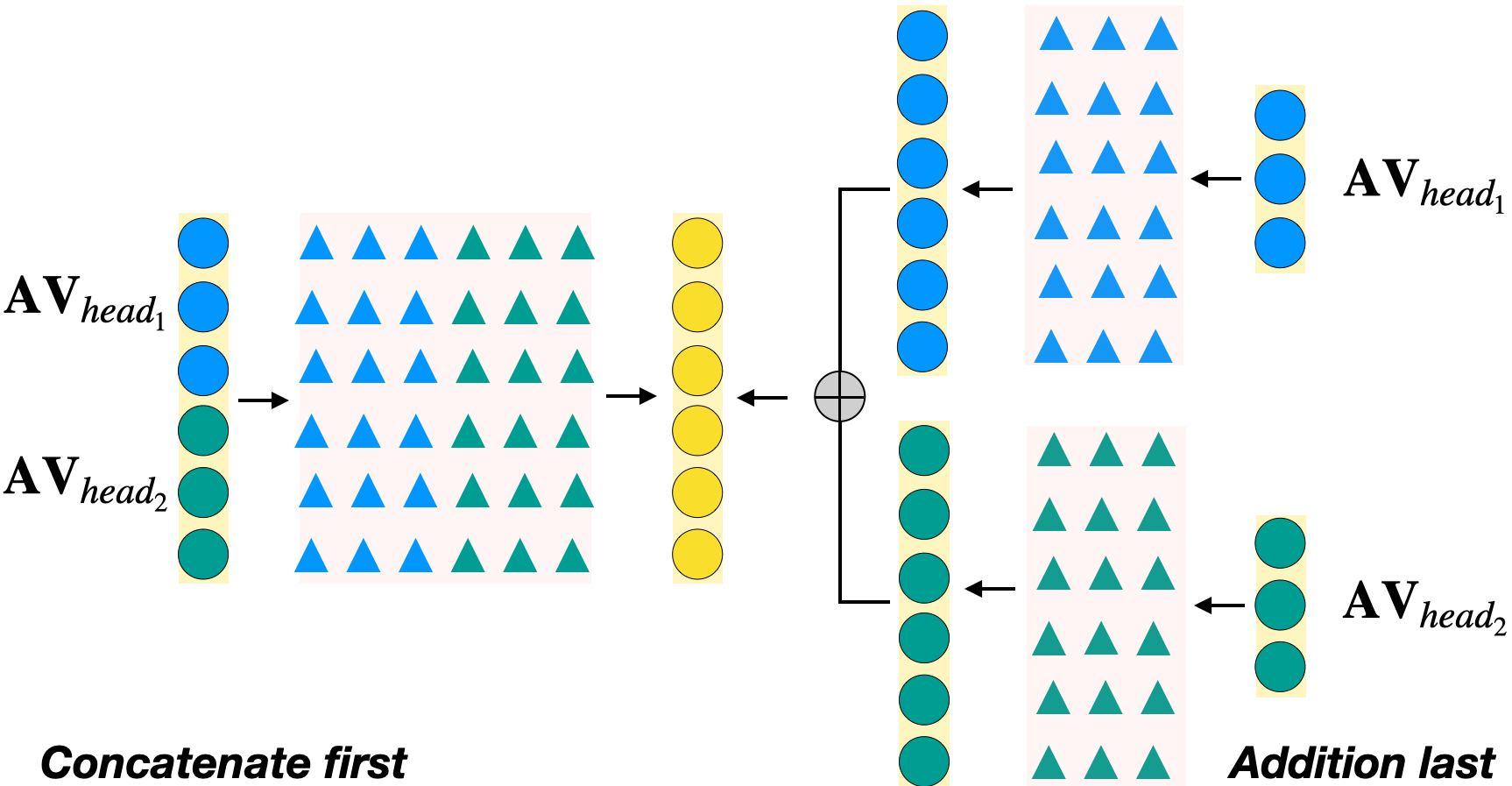
Interpretability is an important aspect of the trustworthiness of a model's predictions. Transformer's predictions are widely explained by the attention weights, i.e., a probability distribution generated at its self-attention unit (head). Current empirical studies provide shreds of evidence that attention weights are not explanations by proving that they are not unique. A recent study showed theoretical justifications to this observation by proving the non-identifiability of attention weights. For a given input to a head and its output, if the attention weights generated in it are unique, we call the weights identifiable. In this work, we provide deeper theoretical analysis and empirical observations on the identifiability of attention weights. Ignored in the previous works, we find the attention weights are more identifiable than we currently perceive by uncovering the hidden role of the key vector. However, the weights are still prone to be non-unique attentions that make them unfit for interpretation. To tackle this issue, we provide a variant of the encoder layer that decouples the relationship between key and value vector and provides identifiable weights up to the desired length of the input. We prove the applicability of such variations by providing empirical justifications on varied text classification tasks. The implementations are available at https://github.com/declare-lab/identifiable-transformers.
翻译:模型预测的可解释性是模型预测的可信任性的一个重要方面。 模型预测的可解释性是一个重要方面。 变换器的预测通过注意权重的广泛解释, 即其自我注意单位( 头部) 产生的概率分布。 目前的经验研究提供了一些证据, 表明注意权重不是通过证明其并非独特的作用来解释的。 最近的一项研究通过证明注意权重的不可识别性, 显示了这一观察的理论理由。 对于给一个头部及其产出提供的投入, 如果它产生的注意权重是独特的, 我们称之为可识别的权重。 在这项工作中, 我们对注意权重的可识别性提供了更深的理论分析和实验性观察。 在以往的工作中,我们忽略了这一点,我们发现注意权重比我们目前所认为的要清楚得多,通过揭示关键矢量的隐藏作用来说明这些重要性。 然而, 重量仍然容易成为不值得解释的非不可辨认的注意。 为了解决这一问题,我们提供了一种变式的编码层, 分解关键矢量和价值矢量之间的关系, 并且提供了可识别的重量。 在以往工作中, 提供不同的经验输入/ 解释性的解释性 。