NeurIPS2023 | AI4Science: Newton–Cotes图神经网络——动态系统上的时间演化

**论文题目：**Newton-Cotes Graph Neural Networks: On the Time Evolution of Dynamic Systems **本文作者：**郭凌冰（浙江大学）、王维清（莫纳什大学）、陈卓（浙江大学）、张宁豫（浙江大学）、孙泽群（南京大学）、赖奕璇（浙江大学）、张强（浙江大学）、陈华钧（浙江大学） **发表会议：**NeurIPS 2023 **论文链接：**https://arxiv.org/abs/2305.14642 代码链接：https://github.com/zjukg/NCGNN 欢迎转载，转载请注明出处

引言

对动态系统时间演化的研究至今已有数百年的历史，尽管计算机的不断发展使得精确模拟由多个外力约束构成的复杂系统成为可能，但大多数研究者仍难以负担其计算成本。最近，许多工作提出了利用图神经网络（GNNs）模型来直接预测系统的未来状态而无需逐步模拟。以分子动力学（Molecular Dynamics）为例，以分子的初始状态作为输入，而分子所包含的原子可以被视为具有不同特征的节点，这些节点可以由GNN进行编码，而特征则为坐标、质量、电荷等信息。由于输入的初始状态和要预测的状态都是原子坐标，这一学习问题就转换成了预测每个原子每个维度的坐标的回归任务。值得注意的是，一些具有方向的信息（如每个原子的速度或受到的力）也是重要的特征。当同一个分子并非总是以特定朝向和初始位置输入时，这些特征便无法直接利用。因此，现有的工作致力于保留和利用分子自身和这些矢量特征的物理对称性（Physical Symmetries），如在欧式空间下的变换等价性（Transformation Equivariance）和几何约束。在各种标准数据集上的实验结果也证明了这种等变图神经网络（Equivariant GNN，EGNN）方法的优势。大多数等变图神经网络的主要目标是预测与初始坐标相距T个时间段的未来坐标，具体可用下述公式表示：

对于由多个粒子构成的复杂系统，预测粒子的速度而非坐标可以提高稳定性和性能。具体而言，通过减去初始坐标，所要预测的目标就变为了归一化的未来坐标，同时也可视为一种残差学习。目前几乎所有先进的等变图神经网络方法都采用这种策略，但以数值积分的角度来看，其仍存在着显著缺陷。方法

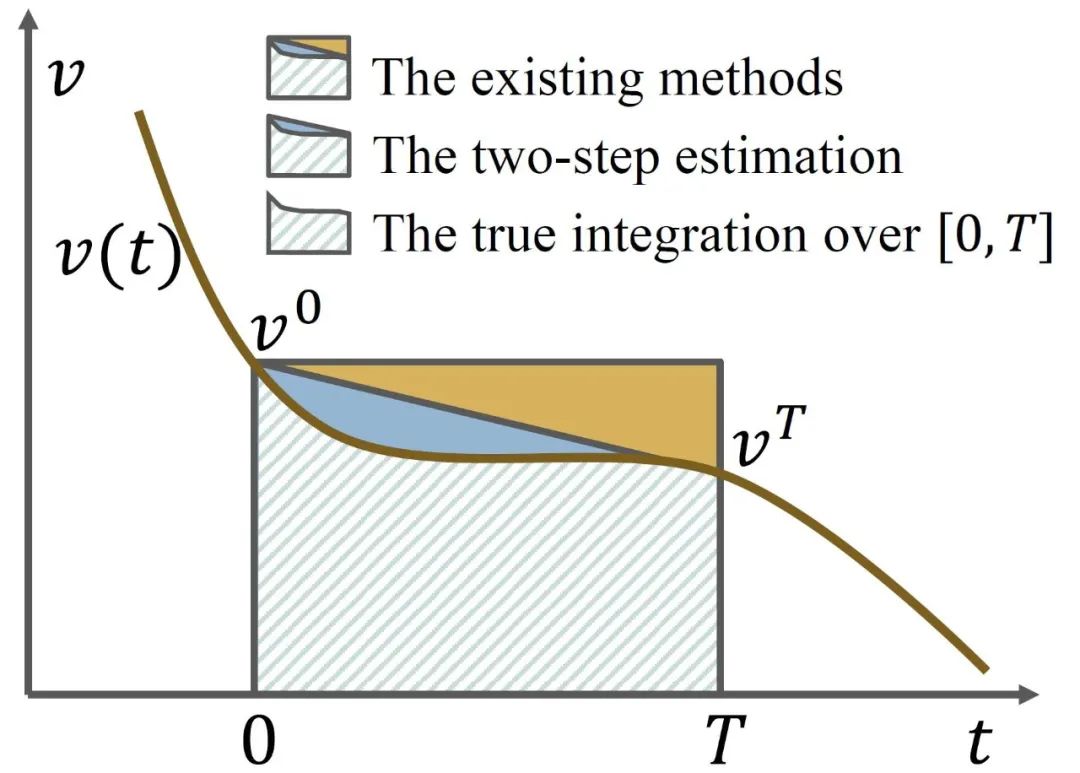
如上图所示，假设粒子的实际速度由曲线可以用来表示，为了预测时刻的未来状态，现有方法采用了一种把速度视为常数的估计方法，即

显然，上述公式更多的是依赖于神经网络的拟合能力，对于速度的估计可能会有很大的偏差。如果能够将单次估计替换为简单的两步估计法（即梯形法则），则误差如图中蓝色区域所示，将会显著减小，进而神经网络模型则仅需要对蓝色区域进行补偿，学习难度大大减小。本文提出的名为Newton–Cotes 图神经网络（NCGNN）的方法就旨在估计多个不同时间点的速度，再利用Newton-Cotes 公式计算积分。Newton-Cotes 公式是一系列用于数值积分的公式，其中被积函数（即）只在等间距的数个时间点上可知。Newton-Cotes 公式最重要的特点之一是通过使用一组权重来对这些时间点上的速度值进行加权求和来近似求解积分，而这组权重与当前的被积函数无关，并且可以通过拉格朗日插值多项式预先计算。具体可表示为：

其中为一组与速度函数无关的权重。为神经网络模型预测的中间速度。整个时间段被平均的分为段，共计个时间点。如果位于的时间点也存在对应的真实数据，则可以进行额外的监督学习：

如果没有对应的监督数据，神经网络模型则可以通过最小化目标损失函数的方式学习到最佳的中间速度值。 实验结果

本文实验在三种不同类型的数据集上验证了NCGNN的性能：即多体系统（N-body)、分子动力学模拟（MD17）、以及人类动作轨迹（Human Motion）。本文还研究了有额外监督数据的情况NC+和无额外监督数据的情况NC，同时还考虑了不同等变图神经网络下的性能差异。

单步预测

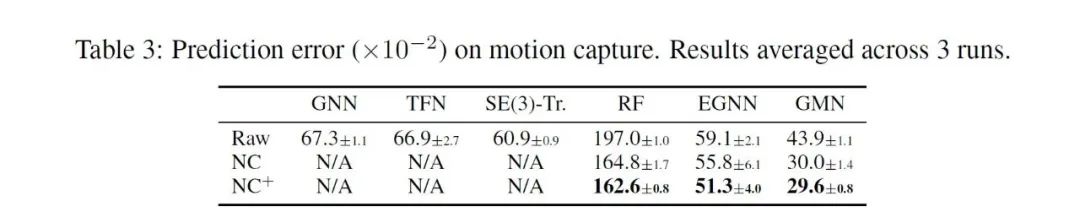
在单步预测实验中，模型需要只根据单个初始时间点的状态预测较远的未来时间点的状态，其结果用平均距离误差来评估。下表分别列举了在三种不同数据集上、不同等变图神经网络下的性能表现：

可以看出，NCGNN可以显著提升三种不同的等变图神经网络模型的性能。在不使用监督数据时，尽管性能有轻微下降，但仍显著优于现有所有方法。

多步预测

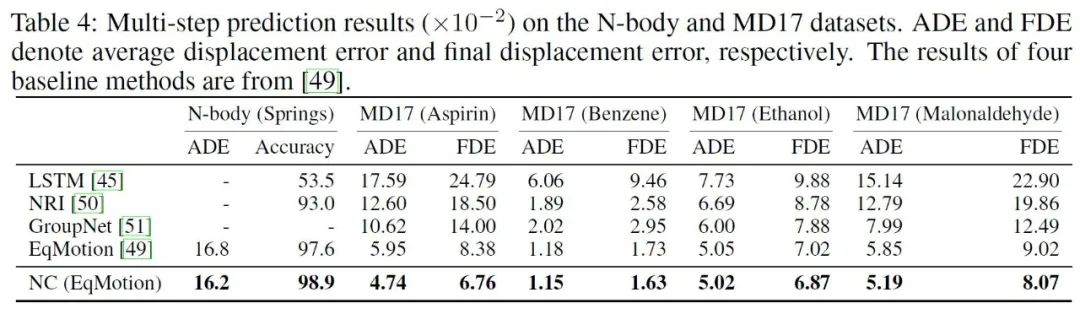
在多步预测实验中，给定连续多步的初始状态，预测接下来同样步数的未来状态。其实验结果如下表所示：

可以看出，NCGNN同样可以显著提升现有的多步预测模型。

动态系统上的时间演化

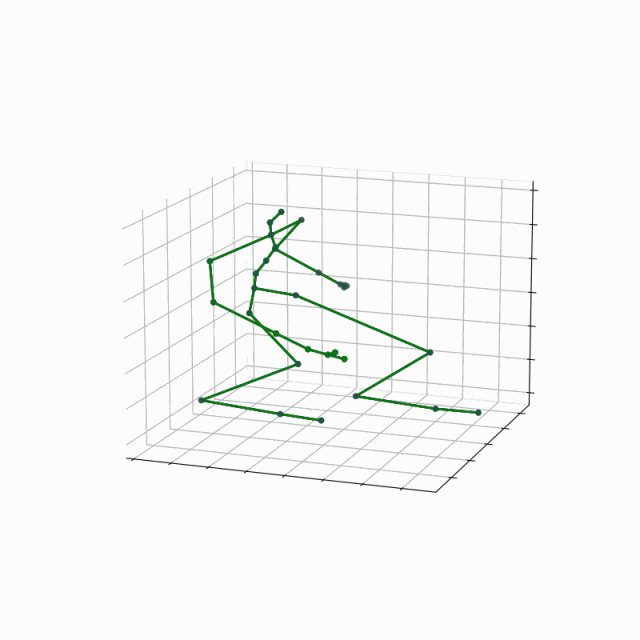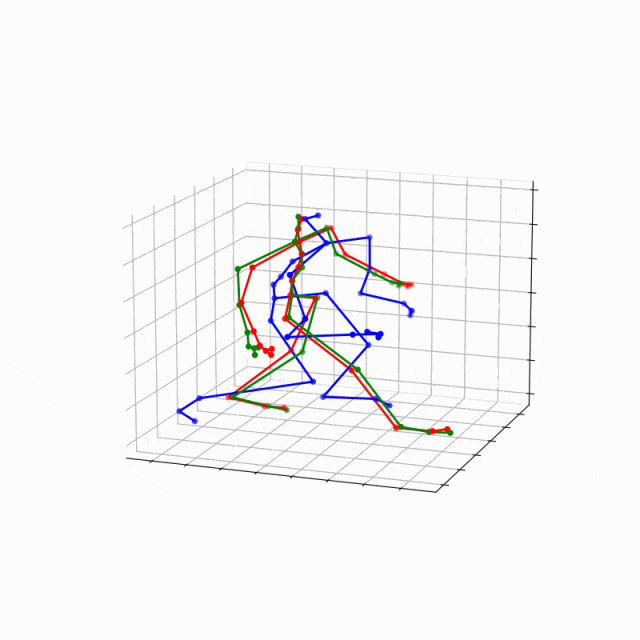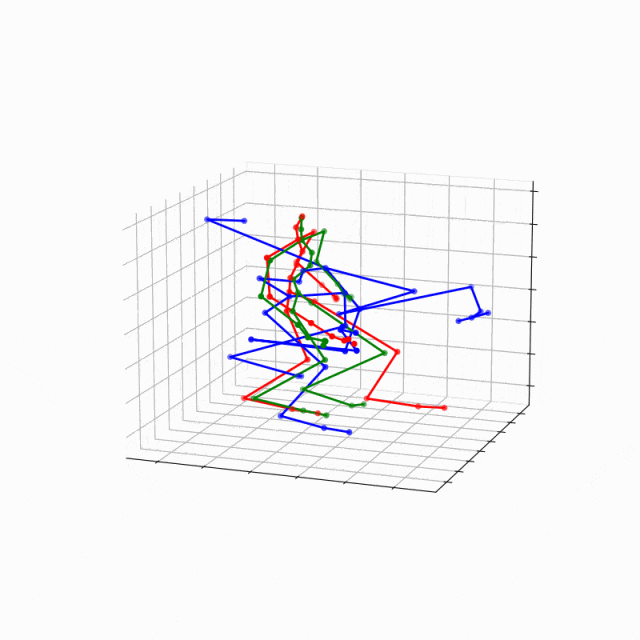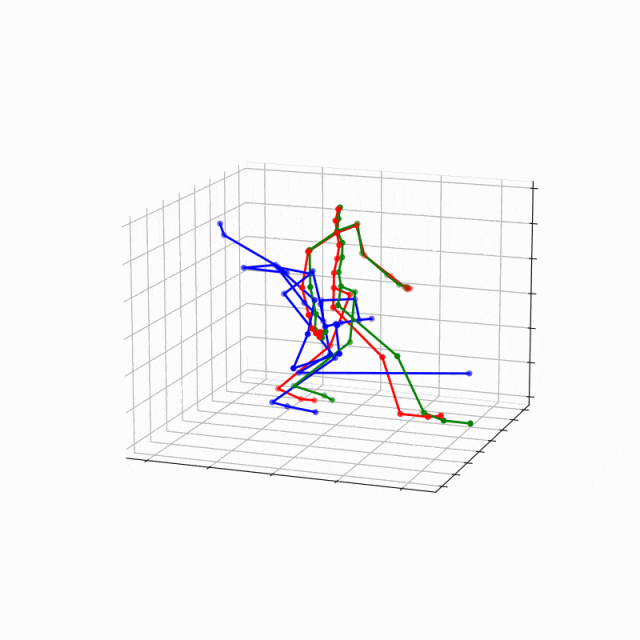
考虑多个时间点上的数据进行监督学习可以学习到更稳定、更精确的连续未来坐标预测。下图为人类动作轨迹数据集上的一个样例，其中红色为目标轨迹，绿色和蓝色则分别为有监督NC+和无监督NC的结果。可以看出，无监督下的模型在最初几步的预测中表现尚且良好，但随着时间的演化迅速崩溃；而有监督的条件下模型一直表现良好。

那么，获取初始时间点与目标时间点之间的监督数据的代价高吗？通常情况下，动态系统的数据都是由采样或者计算机系统模拟得到的，其采样间隔远远小于基于神经网络的方法所学习预测的时间间隔。同时，现实中采样工具以固定频率进行采样，Newton-Cotes 公式假设已知的时间点是严格等距划分的，这也是为什么本文选择Newton-Cotes作为计算工具的原因。因此这些监督数据可以轻易取得。总结

本文提出了一种利用Newton-Cotes 公式来解决推理复杂系统动态演化的方法，并从理论和实验两方面证明其有效性，在多个任务和数据集上均显著优于现有方法。通过提供少量易于获得的额外数据，NCGNN可以生成高质量的连续预测结果。

成为VIP会员查看完整内容