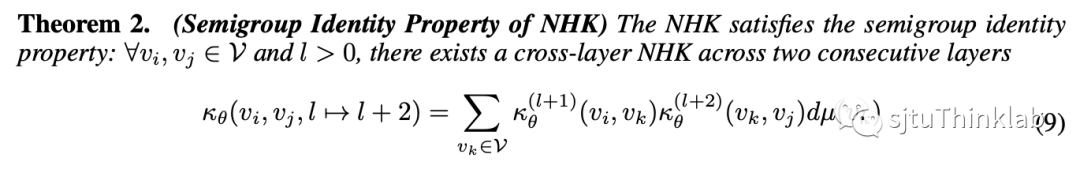论文题目： Geometric Knowledge Distillation: Topology Compression for Graph Neural Networks

作者信息： 杨晨晓 (上海交通大学)，吴齐天 (上海交通大学)，严骏驰 (上海交通大学) 论文链接： https://openreview.net/pdf?id=7WGNT3MHyBm 代码链接： https://github.com/chr26195/GKD

简介

现目前有很多工作开始关注图数据的泛化和迁移问题，然而很少有研究在泛化相关的问题上考虑拓扑信息。在这个工作中，我们提出了一种全新的基于拓扑的知识迁移范式，即几何知识蒸馏（Geometric Knowledge Distillation），它可以实现两个定义在不一致的图拓扑上的图神经网络(GNN)之间实现知识迁移。为了实现这个目标，我们首先回顾了从热力学的角度联系热传导方程（Heat Equation）和图神经网络特征传递的过程。在这一理论框架下，我们提出了神经热核函数 (Neural Heat Kernel, NHK) 将图神经网络背后的流形的几何特性编码成一系列层间的矩阵表示。几何知识蒸馏通过挖掘和对齐教师和学生GNN模型的神经热核，实现将图拓扑信息压缩到模型本身并实现不同GNN之间的知识迁移。我们继而设计了非参数化和参数化的两类模型变种，并在多个图数据知识迁移任务上，如不同图拓扑间的知识迁移、不同大小GNN间的知识蒸馏、通过自蒸馏（Self-Distillation）实现性能提升等，验证了它们的有效性。 TAG： 几何深度学习/ 图神经网络/ 知识蒸馏

从热传导方程到图神经网络

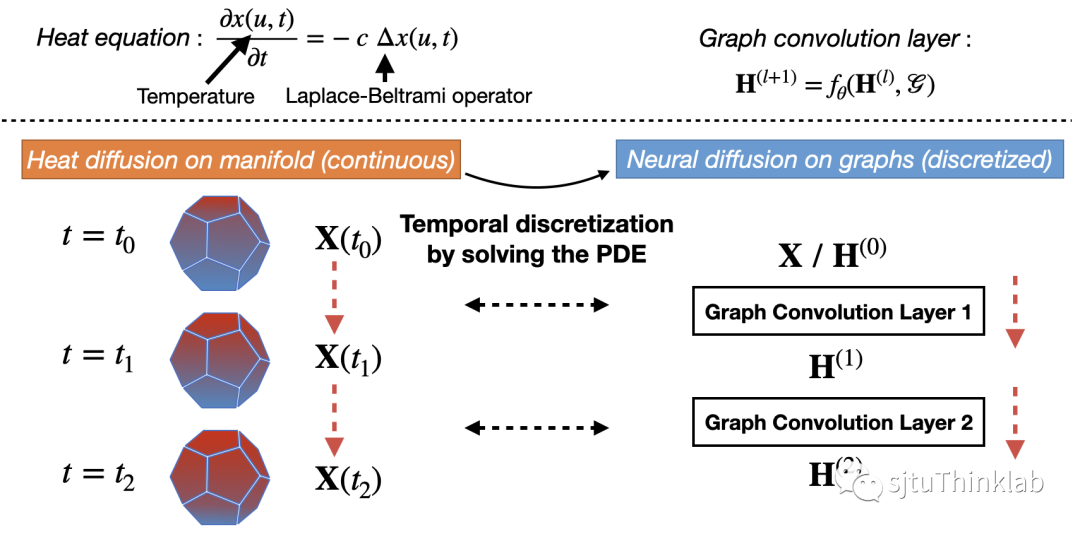
首先，我们简单介绍技术背景。在物理学中，黎曼流形上的热传导过程可以用如下的偏微分方程描述。其中，表示导热系数，: 表示定义在流形上的一个函数，用来表示某个点和时间上的某种信号，例如温度或者其他特征。表示Laplace-Beltrami operator，可以进一步写成 (Divergence operator)和 (Gradient operator)的复合函数（即）。上述偏微分方程的含义可以直观理解为：某一点的信号/温度在无穷小时间间隔内的变化等同于该点信号/温度与其周围区域平均信号/温度的差异。近期，一系列工作 [1-5] 揭示了 GNN 的特征传播过程和底层黎曼流形的热扩散的联系。如下图所示，图拓扑结构（由节点和边构成）可以被看作空间离散化（Spatial discretization）后的黎曼流形，而进一步将热传导方程以数值求解的方法（例如用Euler method求解）进行时间离散化（Temporal discretization）就可以产生一层的 GNN 架构。换句话说，在黎曼流形上一定时间间隔的热传导可以看做一层 GNN 做特征传递（如下图所示）。

另外，不同的定义或者不同的数值求解方法可以产生不同的 GNN 模型结构：例如，将定义为计算相邻节点特征的差值，定义为对特征差值的求和，并用forward Euler method求解热传导方程，就可以得到一层GCN形式 [6] 的特征传递层。

从热核到GNN中的神经热核NHK

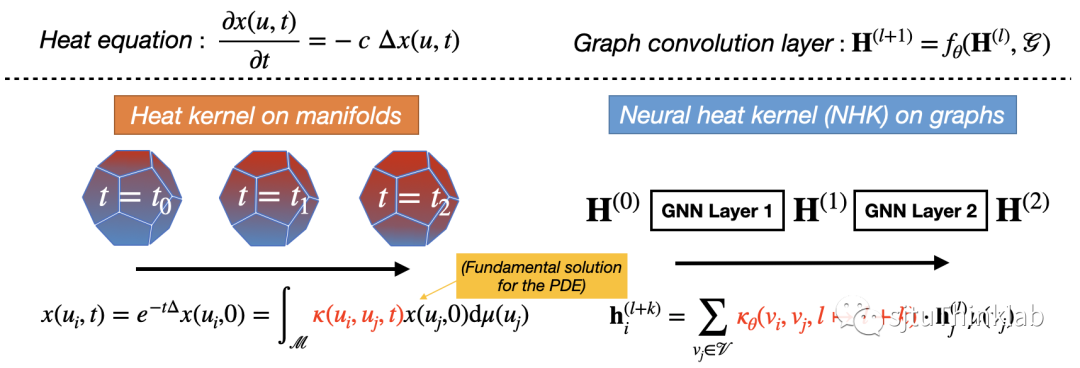
如上所述，用数值求解的方法求解热传导方程可以得到一层 GNN 的信息传递，而有趣的是，给定信号初值，任何黎曼流形上的热传导方程都有唯一的取决于定义的最小正基解，称为热核（Heat kernel），用核函数表示：在物理学中，热核描述了布朗运动在流形上的转移密度，决定了信号如何在流形上进行传播，反应或者刻画了底层流形的几何特征。例如，如果流形是一个维的欧氏空间，热核就可以用高斯核函数的形式表示，而如果流形是一个维的双曲空间，热核就需要用更复杂的核函数形式表示:

本文方法的出发点在于提出了神经热核（Neural heat kernel，NHK），它建立在前文提到的 GNN 和热方程的连接之上，将热核的概念从流形上的热传导拓展到图神经网络（如上图所示）。这一概念从热力学视角使我们能够挖掘 GNN 背后流形的内在几何属性。它的定义如下， NHK 的函数形式由图神经网络对应的决定，而又由上一节所述，图神经网络对应的和图拓扑结构，GNN的定义以及所学的权重有关。因此，正如热核在热传导方程中扮演的角色，我们可以将 NHK 视作一种对 GNN 背后流形的几何特征的刻画，控制信息如何在节点之间流动，这为我们提供了一个数学工具来封装 GNN 模型从图拓扑中提取的几何知识。更直观理解，NHK是一种对特定GNN（“特定”强调固定模型结构和训练参数）背后的图拓扑信息的表示。最后，我们也在 GNN 和热传导联系的视角下严格证明了神经热核的存在：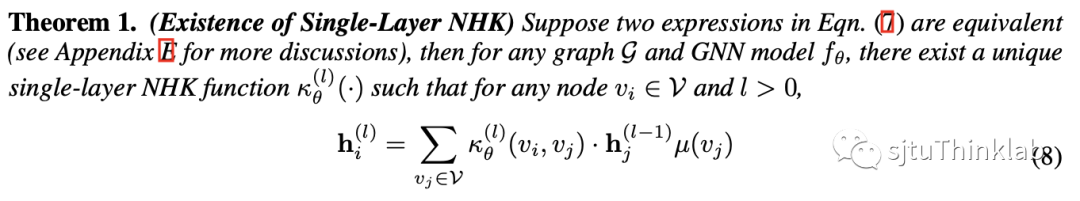

通过NHK实现几何知识蒸馏

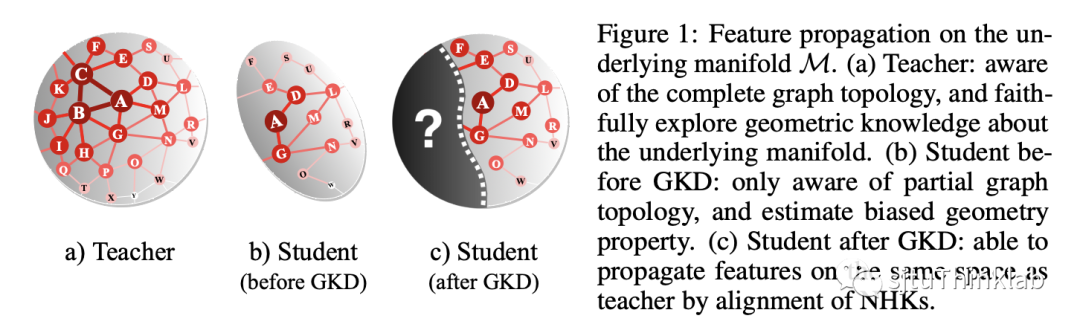
NHK作为一个新的理论工具，我们可以将它用于不同GNN模型间基于图拓扑的知识迁移任务，我们称之为几何知识蒸馏或几何知识迁移。几何知识蒸馏定义为：考虑一个用于节点预测的图神经网络，相对于在训练阶段可以见到完整的图结构，它在测试阶段只能见到一部分的图拓扑结构（包括边信息和节点信息）：我们的目标是将从中提取的几何知识迁移或编码到只知道的目标 GNN 模型。这个问题也对应了一些实际场景中的应用，例如：通过图拓扑压缩在不影响 GNN 模型有效性的情况下提高预测效率，社交推荐或者联邦学习中的隐私限制场景，应对图拓扑结构的动态偏移等等。实现这一目标并非易事，因为我们需要首先找到一种根本性的方法来编码 GNN 模型提取的几何知识，这需要深入研究图拓扑在整个消息传递过程中的作用。因此，我们利用上述热力学的观点，将特征传播解释为底层黎曼流形上的热流，并利用 NHK 来表示图神经网络从图拓扑结构中提取出来的几何知识。基于此，我们提出一个新的知识蒸馏/迁移框架，成为几何知识蒸馏（Geometric knowledge distillation, GKD），它的 motivation 如下图所示：

几何知识蒸馏旨在对齐 GNN 模型之间背后的流形几何特征，将教师 GNN 模型的几何知识迁移给学生 GNN 模型，这样学生模型就可以在同样的底层流形上传播特征，即使它不知道完整的图拓扑信息。在实际操作上，我们定义如下的蒸馏损失函数来对齐教师 GNN 模型和学生 GNN 模型的 NHK matrices：其中表示 NHK 矩阵，计算两个矩阵的 Frobenius distance，是一个加权矩阵用于根据连通性权衡不同的节点对。实现几何知识蒸馏的另一个挑战是，由于 GNN 在做前馈的时候引入了非线性，我们很难推导出 NHK 的显式表达（事实上，即使对于流形上的热传导方程，也只有一部分特定流形的热核方程能被明确推导出来）。为了规避这个问题，我们为 GKD 提出了两种类型的实现，即非参数化和参数化。非参数化的 GKD 通过对底层空间做出假设来考虑有明确公式的核函数，我们最后得出三种 NHK 实现方式，其中随机化的实现依托于热核函数的展开式：参数化的 GKD 以数据驱动的方式学习 NHK（实际上是一个变分分布）, 得到如下的实现形式：其中是一个可学习的非线性特征映射，我们用一种 EM-style 的训练算法进行学习和优化。在实际测试中，我们发现参数化和非参数化的方法都能取得很好的效果，而非参数化的实现方式更加简单高效。

实验结果

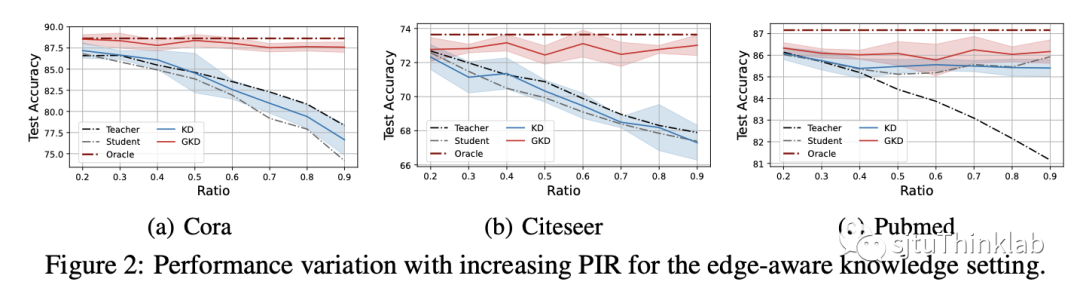
实验设置： 我们在节点分类数据集上进行实验，对比不同类型的（label-based, feature-based, relation-based, graph-based）知识蒸馏算法 [7-10] 以及 Oracle，Teacher，Student 模型。所有方法在测试时均使用不完整的图拓扑信息，除了Oracle模型在测试时可以看到完整的图拓扑信息用于参考对比。我们考虑了两个新实验设定，分别是边几何知识迁移和节点几何知识迁移，其中教师模型分别拥有额外的边信息和节点信息。 主要结果： GKD的所有变体在两个实验设定上都优于其他 KD 算法，并且显著超过 Student 和 Teacher 模型。此外，GKD 及其变体甚至可以与 Oracle 模型相媲美。换句话说，使用 GKD 训练的学生模型可以使用更少的图拓扑信息来实现与在推理过程中了解完整图拓扑的竞争对手非常接近的性能。另外，我们通过额外实验发现 GKD 用于传统的知识蒸馏设定上（即，model compression, self-distillation, online distillation）也依然有效，验证了我们方法的泛用性。部分的实验结果如下图表所示：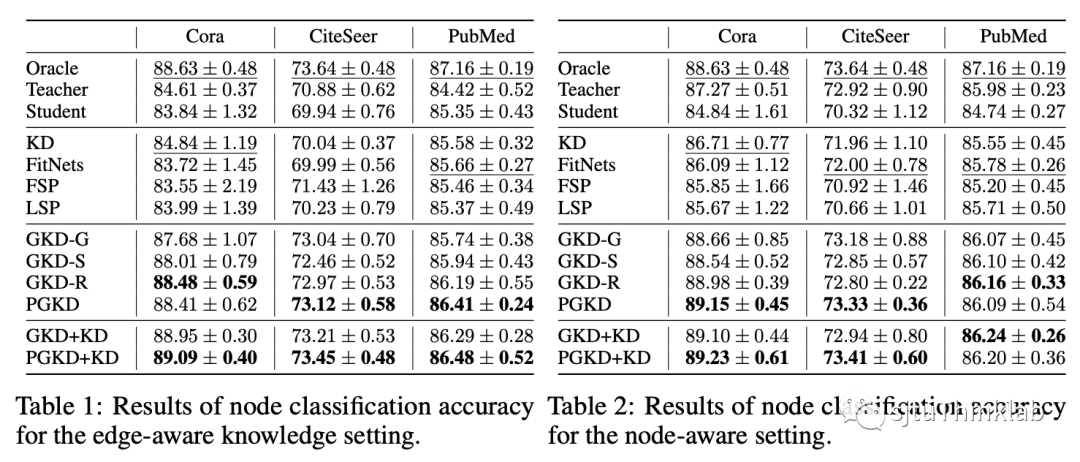

本文亮点总结

本文首次研究了针对GNN的图拓扑知识迁移问题，并提出了神经热核这一理论工具，利用它来表征图的底层流形的几何属性。 * 基于此，本文进而探索了神经热核的一个应用场景，提出了几何知识蒸馏这一框架，它可以将几何知识从教师GNN模型迁移到学生GNN模型。 * 实验结果也验证了我们的方法在各种场景中的有效性，如教师和学生GNN需要处理不同图数据（节点和连边不一致）、具有不同模型大小（参数量不同），或通过自蒸馏提升模型本身性能。

参考文献

Chamberlain, Ben, et al. "Grand: Graph neural diffusion." International Conference on Machine Learning. PMLR, 2021.
Chamberlain, Ben, et al. "Beltrami flow and neural diffusion on graphs." Advances in Neural Information Processing Systems 34 (2021): 1594-1609.
Eliasof, Moshe, Eldad Haber, and Eran Treister. "Pde-gcn: Novel architectures for graph neural networks motivated by partial differential equations." Advances in Neural Information Processing Systems 34 (2021): 3836-3849.
Di Giovanni, Francesco, et al. "Graph neural networks as gradient flows." arXiv preprint arXiv:2206.10991 (2022).
Bodnar, Cristian, et al. "Neural sheaf diffusion: A topological perspective on heterophily and oversmoothing in gnns." Advances in Neural Information Processing Systems (2022).
Kipf, Thomas N., and Max Welling. "Semi-supervised classification with graph convolutional networks." arXiv preprint arXiv:1609.02907 (2016).
Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean. "Distilling the knowledge in a neural network." arXiv preprint arXiv:1503.02531 2.7 (2015).
Romero, Adriana, et al. "Fitnets: Hints for thin deep nets." arXiv preprint arXiv:1412.6550 (2014).
Yim, Junho, et al. "A gift from knowledge distillation: Fast optimization, network minimization and transfer learning." Proceedings of the IEEE conference on computer vision and pattern recognition. 2017.
Yang, Yiding, et al. "Distilling knowledge from graph convolutional networks." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.