【NeurIPS2022】序列(推荐)模型分布外泛化：因果视角与求解

论文题目： Towards Out-of-Distribution Sequential Event Prediction: A Causal Treatment 作者信息： 杨晨晓 (上海交大)，吴齐天 (上海交大)，Qingsong Wen (阿里达摩院)，Zhiqiang Zhou (阿里达摩院)，Liang Sun (阿里达摩院), 严骏驰 (上海交大) 论文链接： https://openreview.net/pdf?id=XQu7UFSbzd2 代码链接： https://github.com/chr26195/Caseq

序列事件预测的目标是根据历史事件序列来估计下一个事件，典型的应用是序列推荐系统，即给定用户的历史点击记录来预测用户下一个可能会点击的商品。在实际场景中，由于数据收集的有限性，往往只能利用某个过去时间窗口内的数据来训练模型，而后模型需要在未来的部署阶段给出预测结果。然而，由于时间和环境的变化，模型从线下训练到上线的过程中会面临分布偏移的挑战，即训练时的数据和部署后的测试数据来自不同的分布，从而导致性能下降。

本文主要探索的问题是：如何训练一个可靠的序列模型，它可以有效泛化到未知分布的测试数据上？ 为此，我们首先从序列数据生成的角度揭示了现有的基于极大似然估计（MLE）训练方法的模型的缺陷：由于数据中潜在的环境因素所带来的bias而无法很好的泛化。对此，我们基于因果干预和后门调整对学习目标进行改进，并进一步利用变分推断得到了一个可求解的新的优化目标。另一方面，我们为这个学习方法设计了一个灵活的模型框架，可以和现有的序列事件预测模型结合在一起，提升模型的分布外泛化能力，并在不同的实验任务上验证了方法的有效性、适用性和可扩展性。

本文的亮点

• 本文首次在事件预测和序列推荐场景中正式定义了分布外泛化的问题，并从因果视角解释了现有模型在此问题中的缺陷，以及揭示了造成该缺陷的本质原因。
• 本文将因果干预和变分推断进行了优雅结合，提出了一个新的学习框架来实现序列预测任务的分布外泛化，该框架具体良好的泛用性，可以和大部分现有的序列预测/推荐模型相结合。
• 本文也提出了新的实验设置来更好地衡量模型的分布外泛化能力，并且通过大量实验验证了时序分布偏移的确会造成模型性能的下降，也同时验证了我们的方法在该场景下的有效性。

时序分布偏移的定义

首先，我们介绍一下背景和问题定义。序列事件预测（Sequential event prediction）[1,2] 是一类经典的任务，其目的是给定历史事件序列（Historical event sequence，用随机变量 表示）时预测下一个事件（Next event，用随机变量 表示）。这个任务对应的应用场景包括序列推荐、设备维护和临床治疗等。例如，在序列推荐中，推荐模型需要根据用户的历史点击记录来预测用户下一个可能会点击的商品来进行推荐。

在这个工作中我们发现，由于此类任务的一个特点是训练和测试数据通常是在不同的时间生成的（例如线下训练的模型需要部署到线上环境），因此随着时间推移，一些未知的外部环境因素（本文称为 Context，用随机变量 表示）会发生变化，进而导致了数据分布的变化。 这个现象反映到现实当中的一个体现是线下训练的模型部署到线上会出现明显的性能下降。在本文中，我们称这类问题为时序分布偏移（Temporal distribution shift），并旨在从根源上分析现有方法的不足和可能的解决方案。 该问题的正式定义如下，假设训练数据从分布 中生成，其中 表示生成第 个训练样本的特定环境，我们的目标是训练一个预测模型 使其可以泛化到来自新分布 的测试数据中，其中 表示第 个测试样本的环境变量。解决这个问题有两个关键困难。首先，由于模型在训练阶段对测试的数据是严格不可见的，因此模型需要具备泛化到未知分布数据的能力。其次，在大部分情况下环境变量 在实际中是不可见的，这也为如何训练一个不受环境的改变所影响的模型增加了困难。例如在推荐场景中， “时尚潮流” 和 “大众偏好”就是常见的环境因素，他们会随着时间的推移发生变化，进而促使用户偏好（即数据分布）的变化。但由于他们只是一种抽象概念，在实际数据中很难收集或记录，模型在训练阶段就只能从观测到的用户交互数据中推断潜在的环境因素。

分析和理解现有方法的缺陷

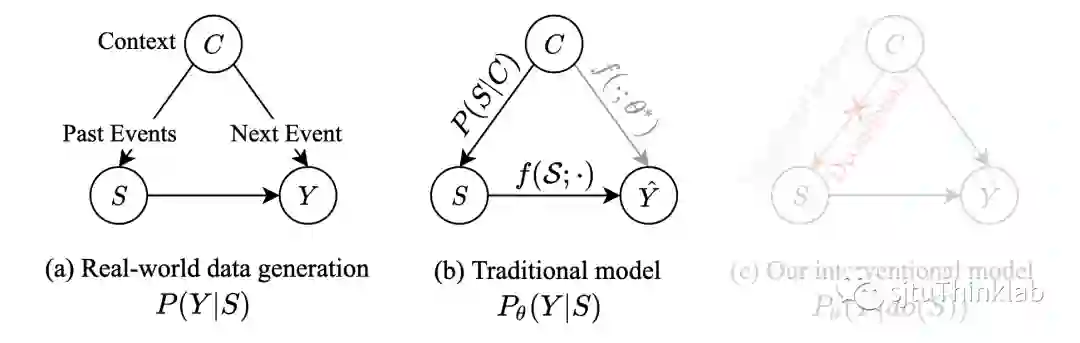
大多数现有的序列预测模型都是基于极大似然估计（即，最大化 ）进行训练和预测的。相应的，我们可以构建数据生成过程中和模型训练时变量之间的因果图（图a：数据生成，图b：模型训练）：

对于数据生成而言，我们有 ，即 依赖于 ，而 同时依赖于 和 ，得到图 a 所示的现实世界中数据生成的因果图。而对于模型训练而言，一方面在建模时，预测模型 将历史事件序列 作为输入，另一方面在使用极大似然估计训练后，模型参数 受到 分布的影响，即： 最终得到了图 b 所示的模型训练和预测的因果图。可以看到，在两张因果图中，变量 是另外两个变量的共因，即干扰变量（Confounder）。其对应的后门路径 将历史事件序列（）和下一个事件（）虚假关联了起来（Spurious correlation）。更直白的讲，由于这种虚假关联的存在，模型在训练阶段很容易学习到和之间的这层虚假相关（即由产生的关联，特定于训练数据），当模型迁移到新的测试分布上时，由于环境（导致了和的实际关联性发生了变化），模型的性能就会下降。

为了更直观的理解干扰变量的负面影响，我们考虑一个如下图所示的例子：在序列推荐场景中，夏季收集的数据可能会将用户购买 “冰淇淋” 和购买 “T 恤” 两类事件“虚假”关联起来，不是因为喜欢吃 “冰淇淋” 的用户都喜欢穿 “T 恤”，而是两类行为在 “夏季” 的环境中都更常见。因此，一旦测试环境转变为 “冬季”，学习到了 “夏季” 中变量之间关联的模型就可能会做出不准确的预测，比如向购买过“冰淇淋”的用户推荐“T恤”，而实际上这个用户在“冬季”购买 “冰淇淋”是因为他是一个甜品爱好者，这时候应该向他推荐其他甜品才会是一个更好的结果。后者所体现的就是历史行为与推荐目标之间的因果关系，他不会随着外在环境的变化而发生改变，这也是我们希望模型真正学到的与之间的关系，从而具备分布外泛化的能力。

分布外泛化的因果干预方案

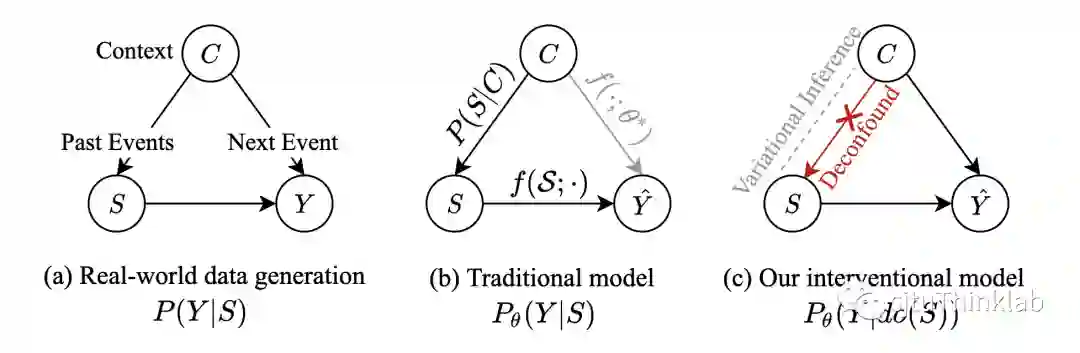
为了解决上述提到的时序分布偏移问题，提高模型分布外泛化的能力，我们引入 算子 [3] 对变量进行因果干预（Causal intervention），提出使用 而不是传统的 作为优化目标。如下图 c 所示，这个操作切断了从 指向 的箭头，阻断了引起 和 之间虚假关联的后门路径 ，使得模型更倾向于学习两个变量之间的直接因果关系:

关于如何理解因果干预，该操作本质上模拟了一个理想的数据生成过程。在这个理想的过程中，我们人为操控序列 ，使其不受环境变量 的影响，例如操控用户在任何季节都有相同的概率购买过棉衣和T恤，平等罗列所有的情况并重新收集数据，从而避免模型额外捕捉由环境引起的虚假关联。类似上述的做法称为随机对照试验（Randomized controlled trial，RCT）[4]，是一种理论上可行的因果干预方式。但是我们知道，现实中我们既无法人为控制环境，也无法要求产生非偏的理想数据，因此不可能通过这种做法来准确计算 。

另一个替代解决思路是利用后门调整（Backdoor adjustment）[8] 来对 进行统计估计，得到以下式子：

直观上理解，后门调整利用独立于 变量的先验 对求和里的每一项重新加权，以此来抵消环境 对数据生成的影响。然而，直接使用这种做法在现有建模框架下是不可行的，因为正如上文所说，大部分环境变量 不同于上述例子中的 “季节” 简单直观，它很有可能是观测不到的，甚至没有现存的定义，更何况先验分布 也是未知的。这成为了使用因果干预的技术难点。 对此，我们提出 Variational context adjustment 方法，利用变分推断引入新的分布 作为给定输入事件序列时对隐变量 的概率估计。基于此，本文通过理论推导得到以下的 ELBO（Evidence lower bound）作为替代 的优化目标：

通过抬高这个 ELBO，一方面可以推动 去挖掘序列背后的环境变量使目标逼近真实的 ，另一方面优化 来实现想要的因果干预和模型分布外泛化。

在实际建模中，我们需要考虑式子中高亮的三个部分：对于 ，我们引入额外的参数化模块（文中称作 Branching unit）来以数据驱动的方式从历史序列 中挖掘离散化的抽象环境变量 。对于 ，我们可以使用任何现有的序列预测模型作为主干（例如 Transformer）来实现（文中称作 Branching unit），用来学习特定环境下历史序列 的低维表示。同时，我们也引入一个 “多层分枝” 结构来考虑更多的（指数级）可能的环境种类，并建模环境之间的联系。最后，对于 ，我们采用了 Mixture of posteriors [5] 的做法来更高效的估计一个更准确的环境先验分布。感兴趣的读者可以参见本工作的原文来更详细地了解。

实验结果

实验设置： 传统的事件预测实验设置将预测不同序列的最后一个事件作为测试集，即，用 1 到 t-1 时刻的历史事件序列预测 t 时刻的未来事件，而剩余的 1 到 t-1 部分用作训练和验证集。但我们发现，该指标没有考虑分布偏移带来的影响，造成线下训练时高估了模型在真实分布外环境下的性能。因此，本文拓展了上述的实验设置，扩大训练和测试之间的间隔，衡量模型在未来时刻/分布外环境中的性能：即在训练集同样的情况下，衡量用 1 到 t-1+d 时刻的历史事件序列预测 t+d 时刻的未来事件，d 对应了具体定义请参见原文。另外，我们在三类序列事件预测任务上对我们的框架进行了实验，包括最主要的序列推荐任务，以及额外的用户事件预测和设备维护任务。我们使用不同的现有模型作为主干网络，并测试的性能提升。

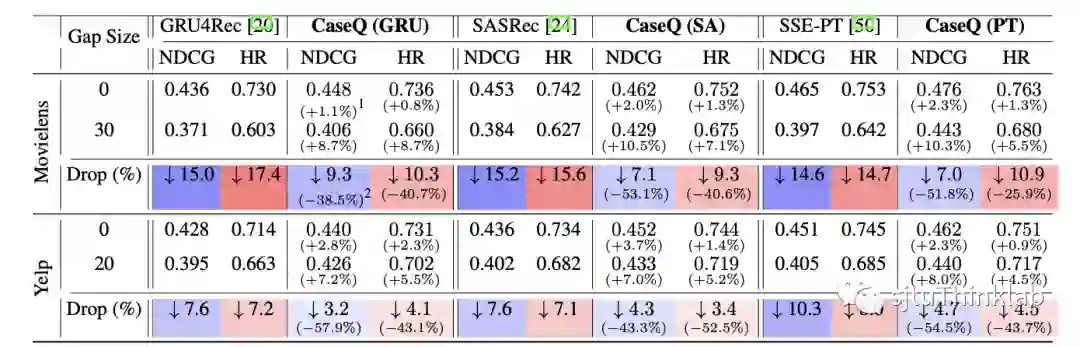
主要结果： 当训练和测试的时间跨度（表中的 Gap Size）变大时（即，时序分布偏移更加严重时），我们发现所有的模型性能都出现了明显的下降，这进一步验证了分布偏移确实会对模型性能造成负影响，是一个值得重视但是现阶段没有很好解决的问题。但在绝对性能上，我们的方法在不同任务中都能够有效对主干网络的性能进行一定程度的提升，而在相对性能上，我们的方法随着时间跨度变大性能下降幅度更加小，验证了其应对时序分布偏移的有效性。另外，我们的方法能够和各种现有的序列事件预测相结合并依然有效，体现了它的泛用性。部分的实验结果如下图表所示：

参考文献

1. Benjamin Letham, Cynthia Rudin, and David Madigan. Sequential event prediction. Machine learning, 93(2):357–380, 2013.
2. Hui Fang, Danning Zhang, Yiheng Shu, and Guibing Guo. Deep learning for sequential recommendation: Algorithms, influential factors, and evaluations. TOIS, 39(1):1–42, 2020.
3. Judea Pearl et al. Models, reasoning and inference. Cambridge University Press, 19, 2000.
4. Judea Pearl, Madelyn Glymour, and Nicholas P Jewell. Causal inference in statistics: A primer. John Wiley & Sons, 2016.
5. Jakub Tomczak and Max Welling. Vae with a vampprior. In AISTATS, 2018.