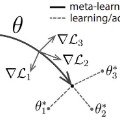
Model-agnostic meta-learning (MAML) is one of the most successful meta-learning algorithms. It has a bi-level optimization structure where the outer-loop process learns a shared initialization and the inner-loop process optimizes task-specific weights. Although MAML relies on the standard gradient descent in the inner-loop, recent studies have shown that controlling the inner-loop's gradient descent with a meta-learned preconditioner can be beneficial. Existing preconditioners, however, cannot simultaneously adapt in a task-specific and path-dependent way. Additionally, they do not satisfy the Riemannian metric condition, which can enable the steepest descent learning with preconditioned gradient. In this study, we propose Geometry-Adaptive Preconditioned gradient descent (GAP) that can overcome the limitations in MAML; GAP can efficiently meta-learn a preconditioner that is dependent on task-specific parameters, and its preconditioner can be shown to be a Riemannian metric. Thanks to the two properties, the geometry-adaptive preconditioner is effective for improving the inner-loop optimization. Experiment results show that GAP outperforms the state-of-the-art MAML family and preconditioned gradient descent-MAML (PGD-MAML) family in a variety of few-shot learning tasks. Code is available at: https://github.com/Suhyun777/CVPR23-GAP.
翻译:摘要: Model-agnostic meta-learning(MAML)是最成功的元学习算法之一。它具有双层优化结构,其中外层流程学习共享初始化权重,内层流程优化特定任务的权重。虽然MAML在内层依赖标准梯度下降,但最近的研究表明,用元学习预处理器控制内层的梯度下降可以产生益处。然而,现有的预处理器不能同时以任务特定和路径依赖的方式适应。此外,它们不满足黎曼度量条件,该条件可以通过预处理梯度启用最陡下降学习。在本研究中,我们提出了几何自适应预处理梯度下降(GAP),它可以克服MAML中的限制。 GAP可以有效地元学习任务特定参数相关的预处理器,其预处理器可以被证明是一个黎曼度量。由于具备两个属性,几何自适应预处理器对提高内部优化非常有效。实验结果表明,GAP在各种少样本学习任务中优于最先进的MAML家族和预处理梯度下降-MAML(PGD-MAML)家族。代码可在以下网址找到:https://github.com/Suhyun777/CVPR23-GAP。