Transferring Knowledge across Learning Processes

Transferring Knowledge across Learning Processes

Sebastian Flennerhag, Pablo G. Moreno, Neil D. Lawrence, Andreas Damianou

(Submitted on 3 Dec 2018 (v1), last revised 22 Mar 2019 (this version, v3))

In complex transfer learning scenarios new tasks might not be tightly linked to previous tasks. Approaches that transfer information contained only in the final parameters of a source model will therefore struggle. Instead, transfer learning at a higher level of abstraction is needed. We propose Leap, a framework that achieves this by transferring knowledge across learning processes. We associate each task with a manifold on which the training process travels from initialization to final parameters and construct a meta-learning objective that minimizes the expected length of this path. Our framework leverages only information obtained during training and can be computed on the fly at negligible cost. We demonstrate that our framework outperforms competing methods, both in meta-learning and transfer learning, on a set of computer vision tasks. Finally, we demonstrate that Leap can transfer knowledge across learning processes in demanding reinforcement learning environments (Atari) that involve millions of gradient steps.

1 INTRODUCTION 

Transfer learning is the process of transferring knowledge encoded in one model trained on one set of tasks to another model that is applied to a new task. Since a trained model encodes information in its learned parameters, transfer learning typically transfers knowledge by encouraging the target model’s parameters to resemble those of a previous (set of) model(s) (Pan & Yang, 2009). This approach limits transfer learning to settings where good parameters for a new task can be found in the neighborhood of parameters that were learned from a previous task. For this to be a viable assumption, the two tasks must have a high degree of structural affinity, such as when a new task can be learned by extracting features from a pretrained model (Girshick et al., 2014; He et al., 2017; Mahajan et al., 2018). If not, this approach has been observed to limit knowledge transfer since the training process on one task will discard information that was irrelevant for the task at hand, but that would be relevant for another task (Higgins et al., 2017; Achille et al., 2018).

We argue that such information can be harnessed, even when the downstream task is unknown, by transferring knowledge of the learning process itself. In particular, we propose a meta-learning framework for aggregating information across task geometries as they are observed during training. These geometries, formalized as the loss surface, encode all information seen during training and thus avoid catastrophic information loss. Moreover, by transferring knowledge across learning processes, information from previous tasks is distilled to explicitly facilitate the learning of new tasks.

 For more demanding tasks, meta-learning in this manner is challenging; backpropagating through thousands of gradient steps is both impractical and susceptible to instability. On the other hand, truncating backpropagation to a few initial steps induces a short-horizon bias (Wu et al., 2018). We argue that as the training process grows longer in terms of the distance traversed on the loss landscape, the geometry of this landscape grows increasingly important. When adapting to a new task through a single or a handful of gradient steps, the geometry can largely be ignored. In contrast, with more gradient steps, it is the dominant feature of the training process.

To scale meta-learning beyond few-shot learning, we propose Leap, a light-weight framework for meta-learning over task manifolds that does not need any forward- or backward-passes beyond those already performed by the underlying training process. We demonstrate empirically that Leap is a superior method to similar meta and transfer learning methods when learning a task requires more than a handful of training steps. Finally, we evaluate Leap in a reinforcement Learning environment (Atari 2600; Bellemare et al., 2013), demonstrating that it can transfer knowledge across learning processes that require millions of gradient steps to converge.

2 TRANSFERRING KNOWLEDGE ACROSS LEARNING PROCESSES We start in section 2.1 by introducing the gradient descent algorithm from a geometric perspective. Section 2.2 builds a framework for transfer learning and explains how we can leverage geometrical quantities to transfer knowledge across learning processes by guiding gradient descent. We focus on the point of initialization for simplicity, but our framework can readily be extended. Section 2.3 presents Leap, our lightweight algorithm for transfer learning across learning processes.

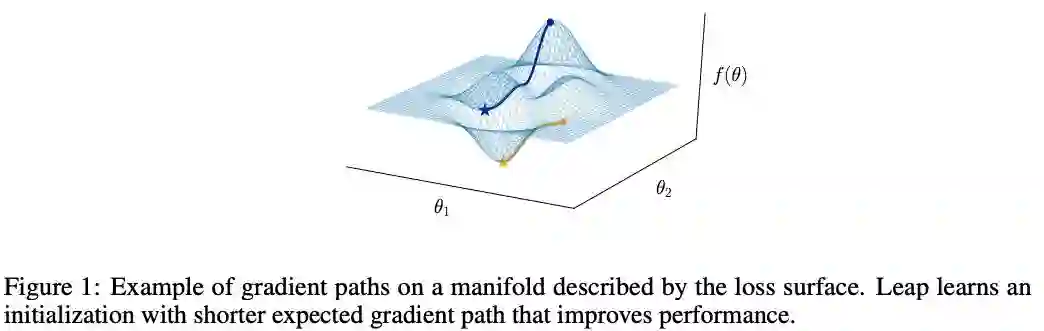
2.1 GRADIENT PATHS ON TASK MANIFOLDS Central to our framework is the notion of a learning process; the harder a task is to learn, the harder it is for the learning process to navigate on the loss surface (fig. 1). Our framework is based on the idea that transfer learning can be achieved by leveraging information contained in similar learning processes. Exploiting that this information is encoded in the geometry of the loss surface, we leverage geometrical quantities to facilitate the learning process with respect to new tasks. We focus on the supervised learning setting for simplicity, though our framework applies more generally. Given a learning objective f that consumes an input x ∈ R m and a target y ∈ R c and maps a parameterization θ ∈ R n to a scalar loss value, we have the gradient descent update as

https://arxiv.org/pdf/1812.01054.pdf