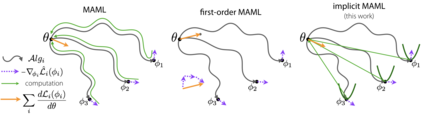
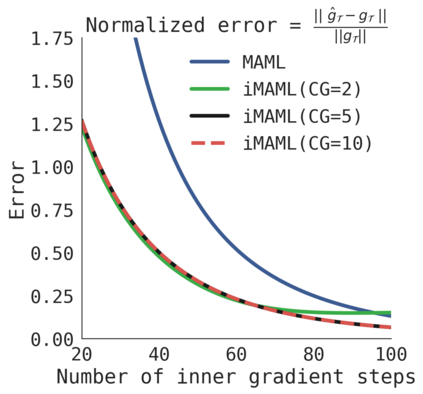
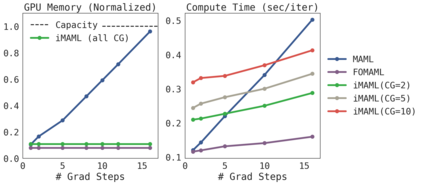
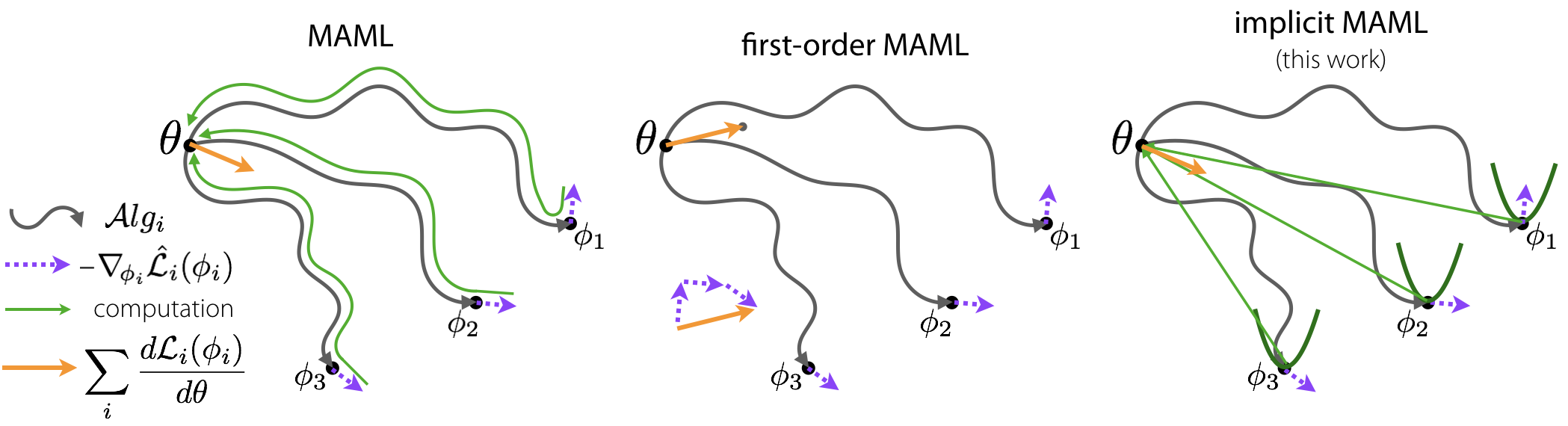
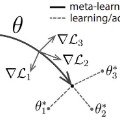
A core capability of intelligent systems is the ability to quickly learn new tasks by drawing on prior experience. Gradient (or optimization) based meta-learning has recently emerged as an effective approach for few-shot learning. In this formulation, meta-parameters are learned in the outer loop, while task-specific models are learned in the inner-loop, by using only a small amount of data from the current task. A key challenge in scaling these approaches is the need to differentiate through the inner loop learning process, which can impose considerable computational and memory burdens. By drawing upon implicit differentiation, we develop the implicit MAML algorithm, which depends only on the solution to the inner level optimization and not the path taken by the inner loop optimizer. This effectively decouples the meta-gradient computation from the choice of inner loop optimizer. As a result, our approach is agnostic to the choice of inner loop optimizer and can gracefully handle many gradient steps without vanishing gradients or memory constraints. Theoretically, we prove that implicit MAML can compute accurate meta-gradients with a memory footprint that is, up to small constant factors, no more than that which is required to compute a single inner loop gradient and at no overall increase in the total computational cost. Experimentally, we show that these benefits of implicit MAML translate into empirical gains on few-shot image recognition benchmarks.
翻译:智能系统的核心能力是通过先前的经验快速学习新任务的能力。 渐进( 优化) 基础元学习最近成为了少数学习的有效方法。 在这种配方中,元参数在外环中学习,而任务特定模型则在内环中学习,只使用当前任务中的少量数据。 推广这些方法的一个关键挑战是需要通过内环学习过程来区分许多梯度步骤,这可能会带来相当大的计算和记忆负担。 通过隐含的差异,我们开发了隐含的MAML算法,该算法仅取决于内部一级优化的解决方案,而不是内部环优化者采用的道路。这有效地将元升级计算与内部环优化的选项选择相分离,而内部环流优化者则只学习少量数据。因此,我们的方法对于选择内环优化器的方法并不敏感,并且可以在不消除梯度或记忆限制的情况下优雅地处理许多梯度步骤。 从理论上说, 我们证明隐含的MAML能够将准确的元等级和记忆足迹进行编译,其记忆足迹只能到内部优化,而不是内部循环优化者所选择的路径, 更能将MLIL 的计算结果,我们所需要的缩缩化的计算。