强化学习的Unsupervised Meta-Learning

Unsupervised Meta-Learning for Reinforcement Learning 

https://www.arxiv-vanity.com/papers/1806.04640/

Abstract

Meta-learning is a powerful tool that builds on multi-task learning to learn how to quickly adapt a model to new tasks. In the context of reinforcement learning, meta-learning algorithms can acquire reinforcement learning procedures to solve new problems more efficiently by meta-learning prior tasks. The performance of meta-learning algorithms critically depends on the tasks available for meta-training: in the same way that supervised learning algorithms generalize best to test points drawn from the same distribution as the training points, meta-learning methods generalize best to tasks from the same distribution as the meta-training tasks. In effect, meta-reinforcement learning offloads the design burden from algorithm design to task design. If we can automate the process of task design as well, we can devise a meta-learning algorithm that is truly automated. In this work, we take a step in this direction, proposing a family of unsupervised meta-learning algorithms for reinforcement learning. We describe a general recipe for unsuper- vised meta-reinforcement learning, and describe an effective instantiation of this approach based on a recently proposed unsupervised exploration technique and model-agnostic meta-learning. We also discuss practical and conceptual consid- erations for developing unsupervised meta-learning methods. Our experimental results demonstrate that unsupervised meta-reinforcement learning effectively ac- quires accelerated reinforcement learning procedures without the need for manual task design, significantly exceeds the performance of learning from scratch, and even matches performance of meta-learning methods that use hand-specified task distributions.

1 Introduction

Reusing past experience for faster learning of new tasks is a key challenge for machine learning. Meta-learning methods propose to achieve this by using past experience to explicitly optimize for rapid adaptation [23, 32, 30, 9, 6, 14, 37, 1]. In the context of reinforcement learning, meta- reinforcement learning algorithms can learn to solve new reinforcement learning tasks more quickly through experience on past tasks [6, 14]. Typical meta-reinforcement learning algorithms assume the ability to sample from a pre-specified task distribution, and these algorithms learn to solve new tasks drawn from this distribution very quickly. However, specifying a task distribution is tedious and requires a significant amount of supervision [10, 6] that may be difficult to provide for large real-world problem settings. The performance of meta-learning algorithms critically depends on the meta-training task distribution, and meta-learning algorithms generalize best to new tasks which

are drawn from the same distribution as the meta-training tasks [8]. In effect, meta-reinforcement learning offloads some of the design burden from algorithm design to designing a sufficiently broad and relevant distribution of meta-training tasks. While this greatly helps in acquiring representations for fast adaptation to the specified task distribution, a natural question is whether we can do away with the need for manually designing a large family of tasks, and develop meta-reinforcement learning algorithms that learn only from unsupervised environment interaction. In this paper, we take an initial step toward the formalization and design of such methods.

Our goal is to automate the meta-training process by removing the need for hand-designed meta- training tasks. To that end, we introduce unsupervised meta-reinforcement learning: meta-learning from a task distribution that is acquired automatically, rather than requiring manual design of the meta-training tasks. Developing effective unsupervised meta-reinforcement learning algorithms is challenging, since it requires solving two difficult problems together: meta-reinforcement learning with broad task distributions, and unsupervised exploration for proposing a wide variety of tasks for meta-learning. Since the assumptions of our method differ fundamentally from prior meta- reinforcement learning methods (we do not assume access to hand-specified meta-training tasks), the best points of comparison for our approach are learning the meta-test tasks entirely from scratch with conventional reinforcement learning algorithms. Our method can also be thought of as a data-driven initialization procedure for deep neural network policies, in a similar vein to data-driven initialization procedures explored in supervised learning [20].

The primary contributions of our work are to propose a framework for unsupervised meta- reinforcement learning, sketch out a family of unsupervised meta-reinforcement learning algorithms, and describe a possible instantiation of a practical algorithm from this family that builds on a recently proposed procedure for unsupervised exploration [7] and model-agnostic meta-learning (MAML) [9]. We discuss the design considerations and conceptual issues surrounding unsupervised meta-reinforcement learning, and provide an empirical evaluation that studies the performance of two variants of our approach on simulated continuous control tasks. Our experimental evaluation shows that, for a variety of tasks, unsupervised meta-reinforcement learning can effectively acquire reinforcement learning procedures that perform significantly better than standard reinforcement learning in terms of sample complexity and asympototic performance, and even rival the performance of conventional meta-learning algorithms that are provided with hand-designed task distributions.

2 Related Work

3 Unsupervised Meta-Reinforcement Learning

The goal of unsupervised meta-reinforcement learning is to take an environment and produce a learning algorithm specifically tailored to this environment that can quickly learn to maximize reward on any task reward in this environment. This learning algorithm should be meta-learned without requiring any human supervision. We can formally define unsupervised meta-reinforcement learning in the context of a controlled Markov process (CMP) – a Markov decision process without a reward function, C = (S,A,T,γ,ρ), with state space S, action space A, transition dynamics T, discount factor γ and initial state distribution ρ. Our goal is to learn a learning algorithm f on this CMP, which can subsequently learn new tasks efficiently in this CMP for a new reward function Ri, which produces a Markov decision processes Mi = (S, A, T, γ, ρ, Ri). We can, at a high level, denote f as a mapping from tasks to policies, f : T → Π, where T is the space of RL tasks defined by the given CMP and Ri, and Π is a space of parameterized policies, such that π ∈ Π is a probability distribution over actions conditioned on states, π(a|s). Crucially, f must be learned without access to any reward functions Ri, using only unsupervised interaction with the CMP. The reward is only provided at meta-test time.

3.1 A General Recipe

Our framework unsupervised meta-reinforcement learning consists of two components. The first component is a task identification procedure, which interacts with a controlled Markov process, without access to any reward function, to construct a distribution over tasks. Formally, we will define the task distribution as a mapping from a latent variable z ∼ p(z) to a reward function rz (s, a) : S × A → R. That is, for each value of the random variable z, we have a different reward function rz(s,a). The prior p(z) may be specified by hand. For example, we might choose a uniform categorical distribution or a spherical unit Gaussian. A discrete latent variable z corresponds to a discrete set of tasks, while a continuous representation could allow for an infinite task space. Under this formulation, learning a task distribution amounts to optimizing a parametric form for the reward function rz (s, a) that maps each z ∼ p(z) to a different reward function.

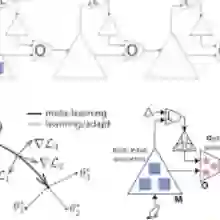
The second component of unsupervised meta-learning is meta-learning, which takes the family of reward functions induced by p(z) and rz (s, a), and meta-learns a reinforcement learning algorithm f that can quickly adapt to any task from the task distribution defined by p(z) and rz(s,a). The meta-learned algorithm f can then learn new tasks quickly at meta-test time, when a user-specified reward function is actually provided. This generic design for an unsupervised meta-reinforcement learning algorithm is summarized in Figure 1.

The nature of the task distribution defined by p(z) and rz (s, a) will affect the effectiveness of f on new tasks: tasks that are close to this distribution will be easiest to learn, while tasks that are far from this distribution will be difficult to learn. However, the nature of the meta-learning algorithm itself will also curcially affect the effectiveness of f. As we will discuss in the following sections, some meta-reinforcement learning algorithms can generalize effectively to new tasks, while some cannot. A more general version of this algorithm might also use f to inform the acquisition of tasks, allowing for an alternating optimization procedure the iterates between learning rz (s, a) and updating f , for example by designing tasks that are difficult for the current algorithm f to handle. However, in this paper we will consider the stagewise approach, which acquires a task distribution once and meta-trains on it, leaving the iterative variant for future work.

3.2 Unsupervised Task Acquisition

Task acquisition via diversity-driven exploration. We can acquire more varied tasks if we allow ourselves some amount of unsupervised environment interaction. Specifically, we consider a recently proposed method for unsupervised skill diversity method - Diversity is All You Need (DIAYN) [7] for task acquisition. DIAYN attempts to acquire a set of behaviors that are distinguishable from one another, in the sense that they visit distinct states, while maximizing conditional policy entropy to encourage diversity [15]. Skills with high entropy that remain discriminable must explore a part of the state space far away from other skills. Formally, DIAYN learns a latent conditioned policy πθ(a|s,z), with z ∼ p(z), where different values of z induce different skills. The training process promotes discriminable skills by maximizing the mutual information between skills and states (MI(s,z)), while also maximizing the policy entropy H(a|s, z):

F(θ) 􏰜 MI(s, z) + H[a | s] − MI(a, z | s) = H[a | s, z] + H[z] − H[z | s] (1)

A learned discriminator Dφ(z|s) maximizes a variational lower bound on Equation 1 (see [7] for proof). We train the discriminator to predict the latent variable z from the observed state, and optimize the latent conditioned policy to maximize the log-likelihood of the discriminator correctly classifying states which are visited under different skills, while maximizing policy entropy. Under this formulation, we can think of the discriminator as rewarding the policy for producing discriminable skills, and the policy visitations as informing the training of the discriminator.

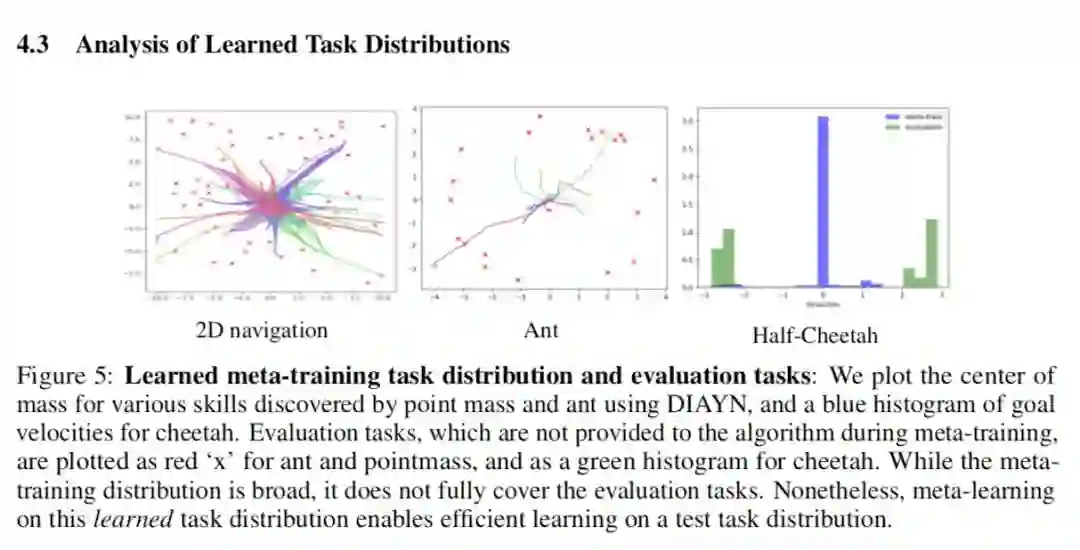
After learning the policy and discriminator, we can sample tasks by generating samples z ∼ p(z) and using the corresponding task reward rz(s) = log(Dφ(z|s)). Compared to random discriminators, the tasks acquired by DIAYN are more likely to involve visiting diverse parts of the state space, potentially providing both a greater challenge to the corresponding policy, and achieving better coverage of the CMP’s state space. This method is still fully unsupervised, as it requires no handcrafting of distance metrics or subgoals, and does not require training generative model to generate goals [16].

3.5 Which Unsupervised and Meta-Learning Procedures Should Work Well?

Having introduced example instantiations of unsupervised meta-reinforcement learning, we discuss more generally what criteria each of the two procedures should satisfy - task acquisition and meta- reinforcement learning. What makes a good task acquisition procedure for unsupervised meta- reinforcement learning? Several criteria are desirable. First, we want the tasks that are learned to resemble the types of tasks that might be present at meta-test time. DIAYN receives no supervision in this regard, basing its task acquisition entirely on the dynamics of the CMP. A more guided approach could incorporate a limited number of human-specified tasks, or manually-provided guidance about valuable state space regions. Without any prior knowledge, we expect the ideal task distribution to induce a wide distribution over trajectories. As many distinct reward functions can have the same optimal policy, a random discriminator may actually result in a narrow distribution of optimal trajectories. In contrast, ... Unsupervised task acquisition procedures like DIAYN, which mediate the task acquisition process via interactions with the environment (which imposes dynamically consistent

We might then ask what kind of knowledge could possibly be “baked” into f during meta-training. There are two sources of knowledge that can be acquired. First, a meta-learning procedure like MAML modifies the initial parameters θ of a policy πθ(a|s). When πθ(a|s) is represented by an expressive function class like a neural network, the initial setting of these parameters strongly affects how quickly the policy can be trained by gradient descent. Indeed, this is the rationale behind research into more effective general-purpose initialization methods [19, 40]. Meta-training a policy essentially learns an effective weight initialization such that a few gradient steps can effectively modify the policy in functionally relevant ways.

The policy found by unsupervised meta-training also acquires an awareness of the dynamics of the given controlled Markov process (CMP). Intuitively, an ideal policy should adapt in the space of trajectories τ, rather than the space of actions a or parameters θ; an RL update should modify the policy’s trajectory distribution, which determines the reward function. Natural gradient algorithms impose equal-sized steps in the space of action distributions [31], but this is not necessarily the ideal adaptation manifold, since systematic changes in output actions do not necessarily translate into system changes in trajectory or state distributions. In effect, meta-learning prepares the policy to modify its behavior in ways that cogently affect the states that are visited, which requires a parameter setting informed by the dynamics of the CMP. This can be provided effectively through unsupervised meta-reinforcement learning.