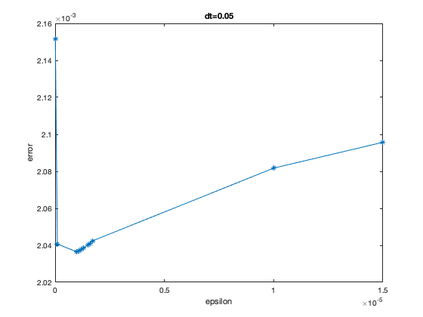
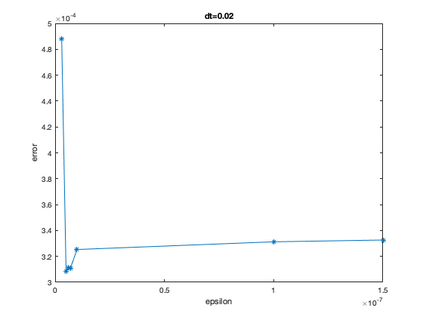
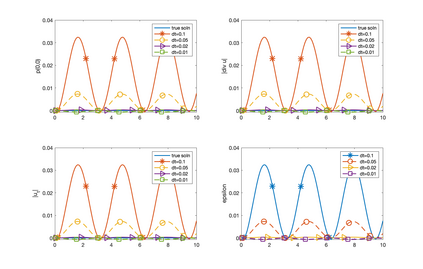
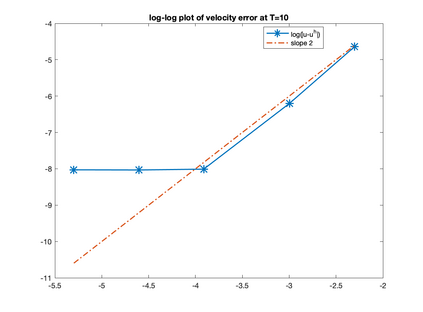
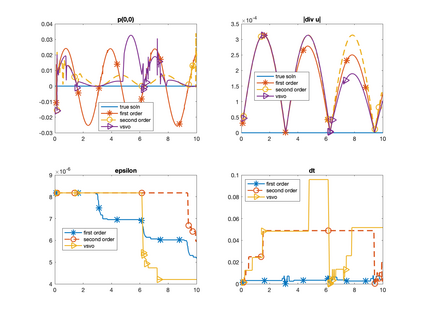
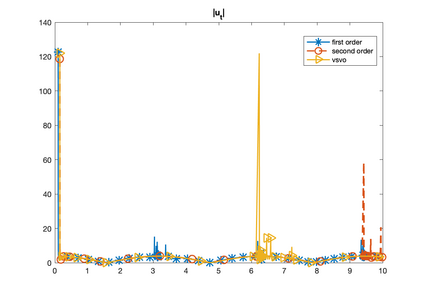
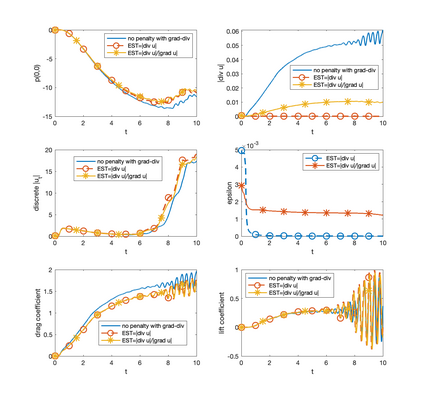
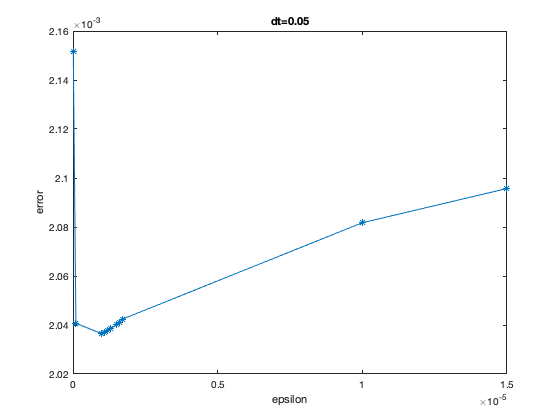
We develop, analyze and test adaptive penalty parameter methods. We prove unconditional stability for velocity when adapting the penalty parameter, $\epsilon,$ and stability of the velocity time derivative under a condition on the change of the penalty parameter, $\epsilon(t_{n+1})-\epsilon(t_n)$. The analysis and tests show that adapting $\epsilon(t_{n+1})$ in response to $\nabla\cdot u(t_n)$ removes the problem of picking $\epsilon$ and yields good approximations for the velocity. We provide error analysis and numerical tests to support these results. We supplement the adaptive-$\epsilon$ method by also adapting the time-step. The penalty parameter $\epsilon$ and time-step are adapted independently. We further compare first, second and variable order time-step algorithms. Accurate recovery of pressure remains an open problem.
翻译:我们开发、分析和测试适应性刑罚参数方法。 当调整处罚参数、 $\ epsilon、 $ 和速度时间衍生物的稳定性时, 在修改处罚参数的条件下, 我们证明对速度的无条件稳定性。 我们提供错误分析和数字测试来支持这些结果。 我们还通过调整时间步骤来补充适应性- $\ $\ en+1 美元的方法。 罚款参数 $\ en+1 美元和时间步骤是独立调整的。 我们进一步比较第一、 第二和变序时间步骤算法。 准确恢复压力仍然是一个未解决的问题 。