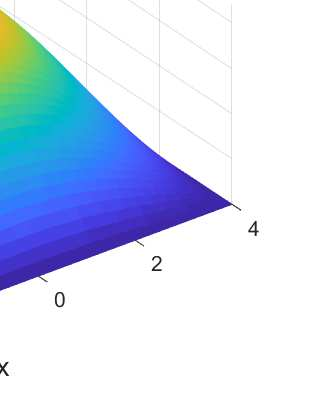
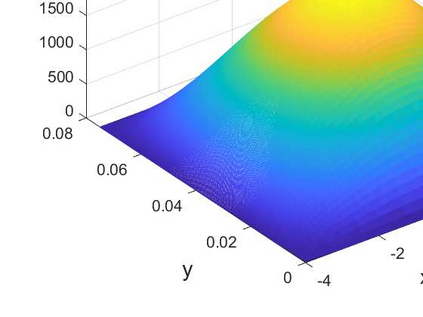
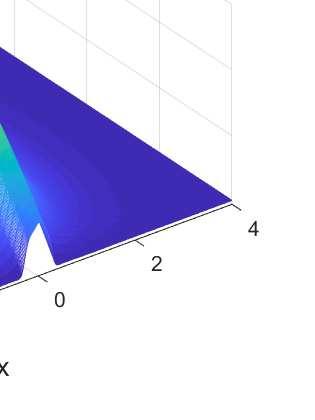
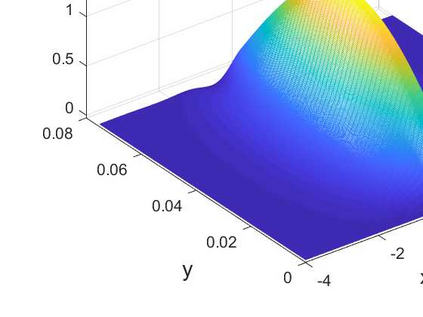
We consider the Cauchy problem for the Helmholtz equation with a domain in R^d, d>2 with N cylindrical outlets to infinity with bounded inclusions in R^{d-1}. Cauchy data are prescribed on the boundary of the bounded domains and the aim is to find solution on the unbounded part of the boundary. In 1989, Kozlov and Maz'ya proposed an alternating iterative method for solving Cauchy problems associated with elliptic,self-adjoint and positive-definite operators in bounded domains. Different variants of this method for solving Cauchy problems associated with Helmholtz-type operators exists. We consider the variant proposed by Mpinganzima et al. for bounded domains and derive the necessary conditions for the convergence of the procedure in unbounded domains. For the numerical implementation, a finite difference method is used to solve the problem in a simple rectangular domain in R^2 that represent a truncated infinite strip. The numerical results shows that by appropriate truncation of the domain and with appropriate choice of the Robin parameters, the Robin-Dirichlet alternating iterative procedure is convergent.
翻译:我们认为,Helmholtz 等式的问题与R ⁇ d、d>2和N圆柱形插件的域有关,与R ⁇ d-1}的域有关,与R ⁇ d-2的域有关,与R ⁇ d-2的域有关,与R ⁇ d-d>2的域有关,与R ⁇ d-d>2的域有关,与R ⁇ d-1}的域有关,与N圆柱形插件有关,与L ⁇ d-ltz类型的域有关,与域的边界有关,对封闭域的边界数据有规定,目的是在边界的无界部分找到解决办法。1989年,Kozlov和Maz'ya提议了一个交替迭代方法,以解决与隔界域的椭圆形、自相交错的域的问题。这个方法的不同变式存在。我们考虑了Mppinganzima et al. 提出的受约束域的域的变式,为在无界域内程序的统一创造了必要的条件。对于数值来说,使用一个有一定的差别的方法在R ⁇ 2的简单矩形域域中解决问题,它代表了细的无限条。数字结果显示,通过适当的域的轨图和选择,Robrin-diridrichlichillentretretretretrevent 程序是相同的程序。