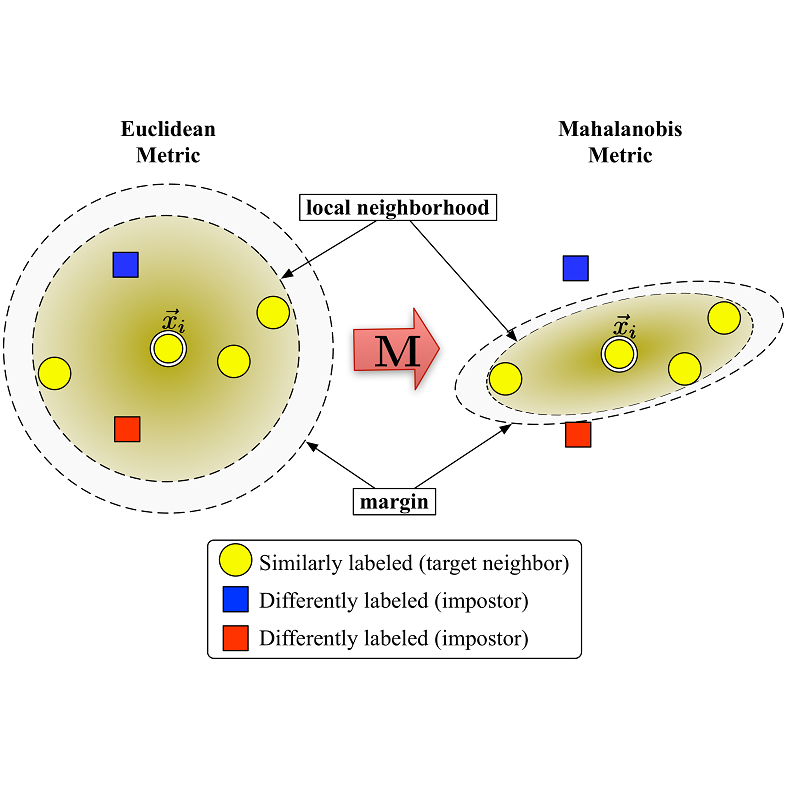
【论文推荐】最新5篇度量学习（Metric Learning）相关论文—人脸验证、BIER、自适应图卷积、注意力机制、单次学习

【导读】专知内容组整理了最近五篇度量学习（Metric Learning）相关文章，为大家进行介绍，欢迎查看!

1. Additive Margin Softmax for Face Verification（基于additive margin softmax的人脸验证方法）

---

---

作者：Feng Wang,Weiyang Liu,Haijun Liu,Jian Cheng

摘要：In this paper, we propose a conceptually simple and geometrically interpretable objective function, i.e. additive margin Softmax (AM-Softmax), for deep face verification. In general, the face verification task can be viewed as a metric learning problem, so learning large-margin face features whose intra-class variation is small and inter-class difference is large is of great importance in order to achieve good performance. Recently, Large-margin Softmax and Angular Softmax have been proposed to incorporate the angular margin in a multiplicative manner. In this work, we introduce a novel additive angular margin for the Softmax loss, which is intuitively appealing and more interpretable than the existing works. We also emphasize and discuss the importance of feature normalization in the paper. Most importantly, our experiments on LFW BLUFR and MegaFace show that our additive margin softmax loss consistently performs better than the current state-of-the-art methods using the same network architecture and training dataset. Our code has also been made available at https://github.com/happynear/AMSoftmax

期刊：arXiv, 2018年1月18日

网址：

http://www.zhuanzhi.ai/document/a0d6140c4d310444ad1f7f12d5facc4d

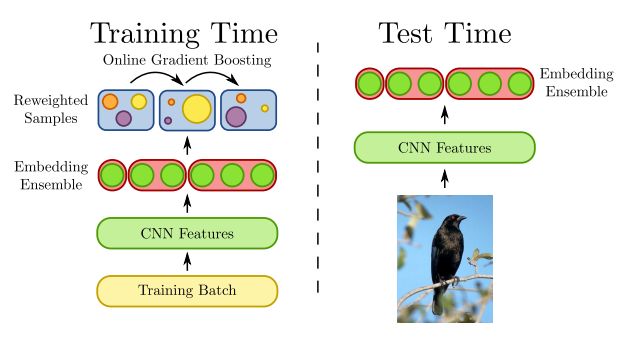
2. Deep Metric Learning with BIER: Boosting Independent Embeddings Robustly（深度度量学习BIER：鲁棒提升独立嵌入方法）

---

---

作者：Michael Opitz,Georg Waltner,Horst Possegger,Horst Bischof

摘要：Learning similarity functions between image pairs with deep neural networks yields highly correlated activations of embeddings. In this work, we show how to improve the robustness of such embeddings by exploiting the independence within ensembles. To this end, we divide the last embedding layer of a deep network into an embedding ensemble and formulate training this ensemble as an online gradient boosting problem. Each learner receives a reweighted training sample from the previous learners. Further, we propose two loss functions which increase the diversity in our ensemble. These loss functions can be applied either for weight initialization or during training. Together, our contributions leverage large embedding sizes more effectively by significantly reducing correlation of the embedding and consequently increase retrieval accuracy of the embedding. Our method works with any differentiable loss function and does not introduce any additional parameters during test time. We evaluate our metric learning method on image retrieval tasks and show that it improves over state-of-the-art methods on the CUB 200-2011, Cars-196, Stanford Online Products, In-Shop Clothes Retrieval and VehicleID datasets

期刊：arXiv, 2018年1月15日

网址：

http://www.zhuanzhi.ai/document/0d512e556a13a04913c59bacb6cf6502

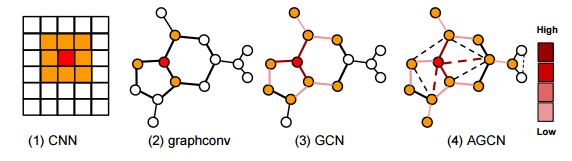
3. Adaptive Graph Convolutional Neural Networks（自适应图卷积神经网络）

---

---

作者：Ruoyu Li,Sheng Wang,Feiyun Zhu,Junzhou Huang

摘要：Graph Convolutional Neural Networks (Graph CNNs) are generalizations of classical CNNs to handle graph data such as molecular data, point could and social networks. Current filters in graph CNNs are built for fixed and shared graph structure. However, for most real data, the graph structures varies in both size and connectivity. The paper proposes a generalized and flexible graph CNN taking data of arbitrary graph structure as input. In that way a task-driven adaptive graph is learned for each graph data while training. To efficiently learn the graph, a distance metric learning is proposed. Extensive experiments on nine graph-structured datasets have demonstrated the superior performance improvement on both convergence speed and predictive accuracy.

期刊：arXiv, 2018年1月10日

网址：

http://www.zhuanzhi.ai/document/17327cb0fa03e8ba0de71fe2b12f86cf

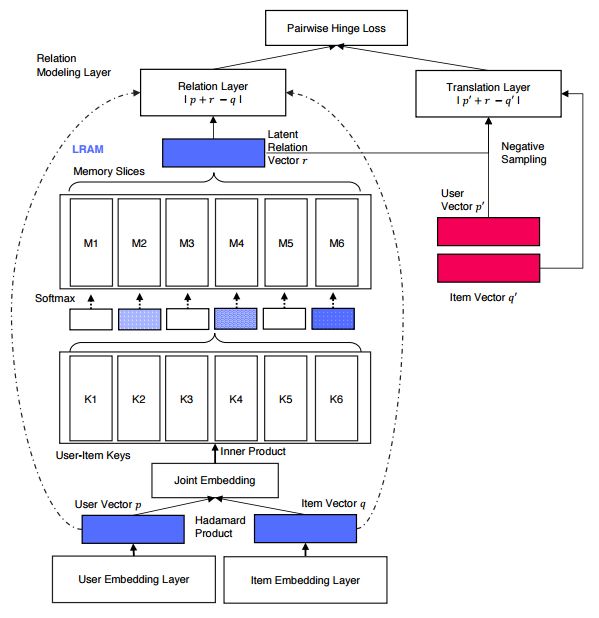
4. Latent Relational Metric Learning via Memory-based Attention for Collaborative Ranking（基于记忆注意力机制的潜在的关系度量学习的协同排序方法）

---

---

作者：Yi Tay,Anh Tuan Luu,Siu Cheung Hui

摘要：This paper proposes a new neural architecture for collaborative ranking with implicit feedback. Our model, LRML (\textit{Latent Relational Metric Learning}) is a novel metric learning approach for recommendation. More specifically, instead of simple push-pull mechanisms between user and item pairs, we propose to learn latent relations that describe each user item interaction. This helps to alleviate the potential geometric inflexibility of existing metric learing approaches. This enables not only better performance but also a greater extent of modeling capability, allowing our model to scale to a larger number of interactions. In order to do so, we employ a augmented memory module and learn to attend over these memory blocks to construct latent relations. The memory-based attention module is controlled by the user-item interaction, making the learned relation vector specific to each user-item pair. Hence, this can be interpreted as learning an exclusive and optimal relational translation for each user-item interaction. The proposed architecture demonstrates the state-of-the-art performance across multiple recommendation benchmarks. LRML outperforms other metric learning models by $6\%-7.5\%$ in terms of Hits@10 and nDCG@10 on large datasets such as Netflix and MovieLens20M. Moreover, qualitative studies also demonstrate evidence that our proposed model is able to infer and encode explicit sentiment, temporal and attribute information despite being only trained on implicit feedback. As such, this ascertains the ability of LRML to uncover hidden relational structure within implicit datasets.

期刊：arXiv, 2018年1月7日

网址：

http://www.zhuanzhi.ai/document/a91ec01604c43c7c4cc5a180c430eceb

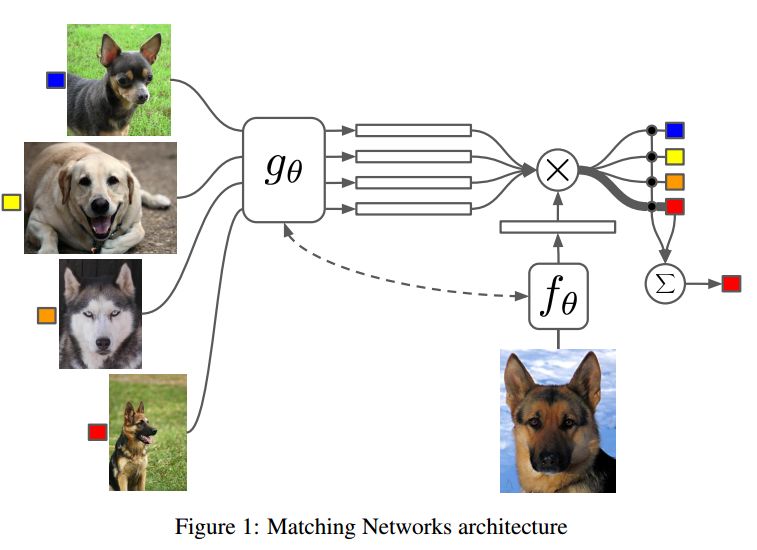
5. Matching Networks for One Shot Learning（匹配网络的单次学习）

---

---

作者：Oriol Vinyals,Charles Blundell,Timothy Lillicrap,Koray Kavukcuoglu,Daan Wierstra

摘要：Learning from a few examples remains a key challenge in machine learning. Despite recent advances in important domains such as vision and language, the standard supervised deep learning paradigm does not offer a satisfactory solution for learning new concepts rapidly from little data. In this work, we employ ideas from metric learning based on deep neural features and from recent advances that augment neural networks with external memories. Our framework learns a network that maps a small labelled support set and an unlabelled example to its label, obviating the need for fine-tuning to adapt to new class types. We then define one-shot learning problems on vision (using Omniglot, ImageNet) and language tasks. Our algorithm improves one-shot accuracy on ImageNet from 87.6% to 93.2% and from 88.0% to 93.8% on Omniglot compared to competing approaches. We also demonstrate the usefulness of the same model on language modeling by introducing a one-shot task on the Penn Treebank.

期刊：arXiv, 2017年12月30日

网址：

http://www.zhuanzhi.ai/document/5d9d504306ebf667d9be7e9392343f82

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

同时欢迎各位用户进行专知投稿，详情请点击：

【诚邀】专知诚挚邀请各位专业者加入AI创作者计划！了解使用专知！

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！

请扫一扫如下二维码关注我们的公众号，获取人工智能的专业知识！

请加专知小助手微信（Rancho_Fang），加入专知主题人工智能群交流！

点击“阅读原文”，使用专知！