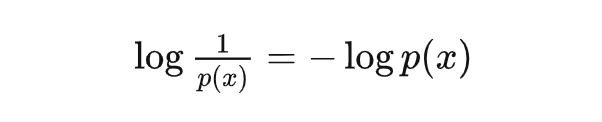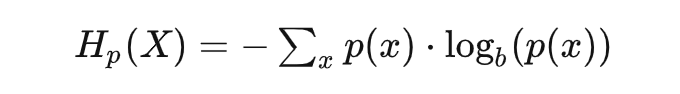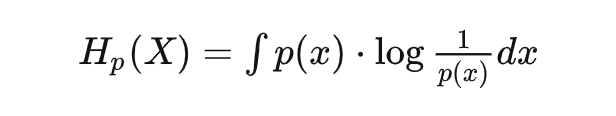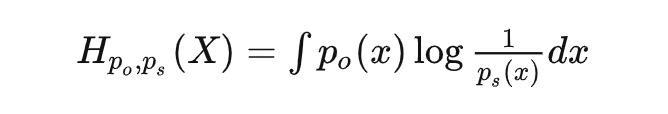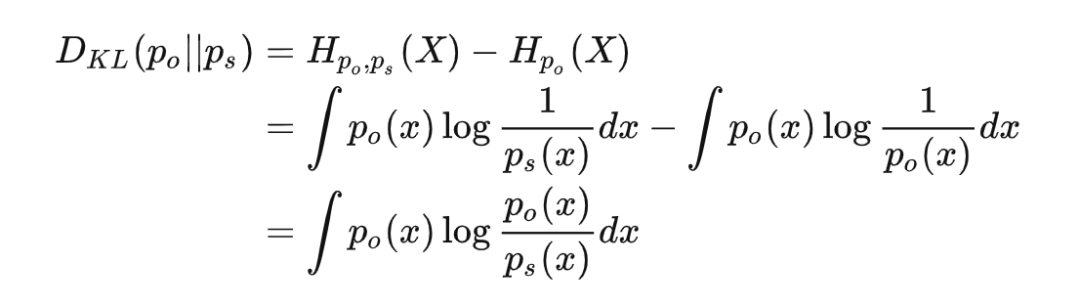一篇文章讲清楚交叉熵和KL散度

©作者 | 康斯坦丁

研究方向 | 信号处理与人工智能

看了很多讲交叉熵的文章，感觉都是拾人牙慧，又不得要领。还是分享一下自己的理解，如果看完这篇文章你还不懂这俩概念就来掐死我吧。

先翻译翻译，什么叫惊喜

我们用 表示事件 发生的概率。这里我们先不讨论概率的内涵, 只需要遵循直觉： 可以衡量事件 发生时会造成的惊喜（行文需要，请按照中性理解）程度 ：

概率越低的事件发生所造成的惊喜程度高；概率越高的事件发生所造成的惊喜程度低。

但是概率倒数这一运算的性质不是很好，所以在不改变单调性的情况下，可以将惊喜度（surprisal）定义为：

这样定义后产生了另外两个好处： 

1. 确定性事件的惊喜度 = 0； 

2. 如果有多个独立事件同时发生，他们产生的惊喜度可以直接相加。是的，一个事件发生概率的倒数再取对数就是惊喜。

信息熵，不过只是惊喜的期望

惊喜度，在大部分文章里，都叫做信息量，但这个命名只是香农根据他研究对象的需要而做的，对于很多其它的场景，要生搬硬套就会变得非常不好理解了。 

信息量 = 惊喜度，那么信息熵呢？看看公式不言自明：

或是连续形式：

这不就是惊喜度的期望吗？

换句话说，信息熵描述的是整个事件空间会产生的平均惊喜。

什么情况下，平均惊喜最低呢？确定事件。以某个离散随机分布为例，整个分布在特定值 为 1，其它处均为 0，此时的信息熵/平均惊喜也为 0。

什么情况下产生的平均惊喜最高呢？自然是不确定越高平均惊喜越高。对于给定均值和方差的连续分布，正态分布（高斯分布）具有最大的信息熵（也就是平均惊喜）。所以再想想为什么大量生活中会看到的随机事件分布都服从正态分布呢？说明大自然有着创造最大惊喜的倾向，或者说，就是要让你猜不透。这也是理解热力学中的熵增定律的另一个角度。

交叉熵，交叉的是古典和贝叶斯学派

对于概率，比较经典的理解是看做是重复试验无限次后事件频率会逼近的值，是一个客观存在的值；但是贝叶斯学派提出了另一种理解方式：即将概率理解为我们主观上对事件发生的确信程度。

针对同一个随机变量空间有两个分布，分别记作   和  ；

 是我们主观认为   会发生的概率，下标   代表 subjective；

 是客观上   会发生的概率，下标 ○ 代表 objective。

这种情况下，客观上这个随机事件   会给我们造成惊喜的期望应该是：

这个量 is a.k.a 交叉熵。 

再翻译一下，交叉熵是什么？ 可 以理解为： 我们带着某个主观认知去接触某个客观随机现象的时候，会产生的平均惊喜度。

那什么时候交叉熵（也就是我们会获得的平均惊喜度）会大？ 就是当我们主观上认为一个事情发生的概率很低 很大)，但是客观上发生概率很高 很大) 的时候，也就是主观认知和客观现实非常不匹配的时候。 机器学习当中为啥用交叉熵来当作损失函数应该也就不言自明了。

相对熵，K-L散度

交叉熵可以衡量我们基于某种主观认识去感受客观世界时，会产生的平均惊喜。但是根据上面的分析，即使主观和客观完全匹配，这时交叉熵等于信息熵，只要事件仍然随机而非确定，就一定会给我们造成一定程度的惊喜。那我们要怎么度量主观认识和客观之间差异呢？可以用应该用以 当前对“世界观”产生的惊喜期望 和完全正确认识事件时产生的惊喜期望的差值来衡量，这个就是相对熵（常称作 KL-散度），通常写作：

当我们的主观认知完全匹配客观现实的时候，KL-散度应该等于 0，其它任何时候都会大于 0。由于存在恒为正这一性质，KL-散度经常用于描述两个分布是否接近，也就是作为两个分布之间“距离”的度量；不过由于运算不满足交换律，所以又不能完全等同于“距离”来理解。

机器学习中通常用交叉熵作为损失函数的原因在与，客观分布并不随参数变化，所以即使是优化 KL-散度，对参数求导的时候也只有交叉熵的导数了。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

📝 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

📬 投稿通道：

• 投稿邮箱：hr@paperweekly.site 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·

·