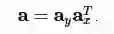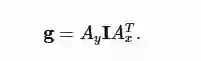神经网络中的「注意力」是什么？怎么用？

概要：神经网络中的注意力机制（Attention mechanisms），也被称为“神经注意力”或“注意力”，最近吸引了广泛的注意力（双关语）。

神经网络中的注意力机制（Attention mechanisms），也被称为“神经注意力”或“注意力”，最近吸引了广泛的注意力（双关语）。而在接下来的这篇文章中，我将描述和实现两种软视觉注意力机制。

什么是注意力（attention）

一种非正式的说法是，神经注意力机制可以使得神经网络具备专注于其输入（或特征）子集的能力：选择特定的输入。这可以是x∈R^d一个输入，z∈R^k一个特征向量，a∈[0,1]^k一个注意力向量或f ϕ (x) 注意力网络。通常来说，注意力为

 

其中⊙是指元素对应乘法（element-wise multiplication）。下面我们可以谈论一下软注意力（soft attention），它将特征与一个值在0和1之间的掩码或当这些值被限定为0或1时的硬注意力（hard attention）相乘，即a∈{0,1}^k。在后一种情况下，我们可以使用硬注意力掩码直接索引特征向量：za =z[a]（用Matlab表示法），可以改变其维度。

如果你想要弄明白为什么注意力机制如此至关重要，那我们就有必要思考一下一个神经网络的真正意义是什么：函数近似器。它的能够近似不同类别函数的能力主要依赖于它的架构。一个典型的神经网络可以被实现为一系列矩阵乘法（matrix multiplications）和元素对应非线性乘法（element-wise non-linearities），其中输入或特征向量的元素仅仅通过加法相互作用。

注意力机制会对一个用于与特征相乘的掩码后进行计算，这种看似简单的额扩展具有深远的影响：突然间，一个可以通过神经网络进行很好的近似的函数空间得到了极大的扩展，使得全新的用例成为可能。为什么会出现这种情况呢？直觉认为是以下原因，虽然没有足够的证据：这种理论认为神经网络是一个通用函数近似器，可以对任意函数进行近似为任意精度，但只能在无限数量的隐藏单位限定条件下进行。而在任何实际情况下，情况并非如此：我们受限于可以使用的隐藏单位的数量。考虑以下示例：我们要对N个输入的结果进行近似，前馈神经网络只能通过模拟具有许多加法（以及非线性）的乘法来实现，因此需要大量神经网络的实际空间。但如果我们引入乘法交互的理念，过程就会自然而然的变得简单而有便捷。 

上述将注意力定义乘法交互（multiplicative interactions）的做法使得我们如果想要放松对注意力掩码值的约束且a∈R^k，可以考虑一种更为广泛的类模型。例如，动态过滤网络（DFN）使用的是一个过滤器生成网络，它是基于输入来计算过滤器（或任意大小的权重），并将其应用于特征，这实际上是一种乘法交互。与软注意力机制的唯一区别就是，注意力权重值没有被限制在0和1之间。想要在这个方向上进行进一步研究，那么去了解哪些交互作用是相加的，哪些是相乘的，探讨加法和乘法神经元之间的可微分转换的概念这都将是非常有趣的。

视觉注意力

注意力可以应用于任何类型的输入而不管其形状如何。在矩阵值输入（如图片）的情况下，我们可以谈论视觉注意力。不管是I∈R^H×W图像还是g∈R^ h×w注意力的一角都可以说是将注意力机制运用于图像的结果。

硬注意力（Hard Attention）

硬注意力在图像中的应用已经被人们熟知多年：图像裁剪（image cropping）。从概念上来看是非常简单的，因为它只需要索引。硬注意力可以用Python（或Tensorflow）实现为：

g = I[y:y+h, x:x+w]

软注意力

软注意力，在其最简单的变体中，对于图像与和向量值来说没有什么不同，并在等式1中得到了完全实现。这种类型的注意力的最早的用途之一是来自于一篇叫做《Show, Attend and Tell》的论文：

 

该模型学习趋向于该图像的特定部分，同时生成描述该部分的单词。

然而，这种类型的软注意力在计算上是非常浪费的。输入的黑色部分对结果没有任何影响，但仍然需要处理。同时它也是过度参数化的：实现注意力的sigmoid 激活函数是彼此相互独立的。它可以一次选择多个目标，但实际操作中，我们经常希望具有选择性，并且只能关注场景中的一个单一元素。由DRAW和空间变换网络（Spatial Transformer Networks）引入的以下两种机制很好地别解决了这个问题。它们也可以调整输入的大小，从而进一步提高性能。

高斯注意力（Gaussian Attention）

高斯注意力通过利用参数化的一维高斯滤波器来创建图像大小的注意力图。使 a y ∈R^h和a x ∈R^w是注意向量，它们分别指定在yy和xx轴中应该出现哪一部分图像。注意力掩码可以创建为：

 

在上图中，顶行显示ax，右边的列显示ay，中间的矩形显示结果a。这里，为了可视化的目的，向量只包含0和1。实际上，它们可以被实现为一维高斯的向量。通常，高斯数等于空间维度，每个向量由三个参数参数化：第一个高斯 μ的中心、连续高斯d的中心距离和高斯标准偏差 σ。通过这个参数，注意力和 glimpse在注意力参数方面是可以区分的，因此很容易学习。

上述形的注意力仍然是浪费的，因为它只选择一部分图像，同时遮挡所有剩余的部分。而不是直接使用向量，我们可以将它们分别放入矩阵 A y ∈R^h×H和 A x ∈R^w×W。现在，每个矩阵每行有一个高斯，参数 d 指定连续行中高斯中心之间的距离（以列为单位）。Glimpse现在实施为：

  

这里是左侧输入图像的示例，注意力glimpse在右侧; glimpse将显示主图像中标记的框为绿色：

 

下面的代码可以为Tensorflow中的一小批样本创建上述矩阵值的掩码。如果要创建Ay，你可以将其称为Ay = gaussian_mask(u, s, d, h, H)，其中u，s，d为该顺序的μ,σ 和 d，以像素为单位指定。

 

def gaussian_mask(u, s, d, R, C):

  """

  :param u: tf.Tensor, centre of the first Gaussian.

  :param s: tf.Tensor, standard deviation of Gaussians.

  :param d: tf.Tensor, shift between Gaussian centres.

  :param R: int, number of rows in the mask, there is one Gaussian per row.

  :param C: int, number of columns in the mask.

  """

  # indices to create centres

  R = tf.to_float(tf.reshape(tf.range(R), (1, 1, R)))

  C = tf.to_float(tf.reshape(tf.range(C), (1, C, 1)))

  centres = u[np.newaxis, :, np.newaxis] + R * d

  column_centres = C - centres

  mask = tf.exp(-.5 * tf.square(column_centres / s))

  # we add eps for numerical stability

  normalised_mask /= tf.reduce_sum(mask, 1, keep_dims=True) + 1e-8

  return normalised_mask

 

我们还可以编写一个函数，直接从图像中提取glimpse：

 

def gaussian_glimpse(img_tensor, transform_params, crop_size):

  """

  :param img_tensor: tf.Tensor of size (batch_size, Height, Width, channels)

  :param transform_params: tf.Tensor of size (batch_size, 6), where params are  (mean_y, std_y, d_y, mean_x, std_x, d_x) specified in pixels.

  :param crop_size): tuple of 2 ints, size of the resulting crop

  """

  # parse arguments

  h, w = crop_size

  H, W = img_tensor.shape.as_list()[1:3]

  uy, sy, dy, ux, sx, dx = tf.split(transform_params, 6, -1)

  # create Gaussian masks, one for each axis

  Ay = mask(uy, sy, dy, h, H)

  Ax = mask(ux, sx, dx, w, W)

  # extract glimpse

  glimpse = tf.matmul(tf.matmul(Ay, img_tensor, adjoint_a=True), Ax)

  return glimpse

 

空间变换（Spatial Transformer）

 

空间变换（STN）允许进行更多的普通变换，与图像裁剪只有细微区别，但是图像裁剪是可能的用例之一。它由两个要素组成：网格生成器和采样器。网格生成器指定网格的点被采样，而采样器，只采样点。

 

def spatial_transformer(img_tensor, transform_params, crop_size):

  """

  :param img_tensor: tf.Tensor of size (batch_size, Height, Width, channels)

  :param transform_params: tf.Tensor of size (batch_size, 4), where params are  (scale_y, shift_y, scale_x, shift_x)

  :param crop_size): tuple of 2 ints, size of the resulting crop

  """

  constraints = snt.AffineWarpConstraints.no_shear_2d()

  img_size = img_tensor.shape.as_list()[1:]

  warper = snt.AffineGridWarper(img_size, crop_size, constraints)

  grid_coords = warper(transform_params)

  glimpse = snt.resampler(img_tensor, grid_coords)

  return glimpse

 

高斯注意力（Gaussian Attention）与空间变换（Spatial Transformer）

 

高斯注意力和空间变换都可以实现非常相似的行为。我们如何选择使用哪一个？这里有几个细微差别：

 

•高斯注意力是一个超参数的裁剪机制：它需要六个参数，但只有四个自由度（y、x、height 、width）。空间变换（STN）只需要四个参数。

 

•我还没有运行任何测试，但是STN应该更快。它依赖于采样点的线性插值，而高斯注意李必须执行两个巨大的矩阵乘法。STN可以快一个数量级（以输入图像的像素为单位）。

 

•高斯注意力应该（没有测试运行）更容易训练。这是因为所发生的glimpse中的每个像素可以是源图像相对大的像素块的凸组合，这样可以更容易地找到任何错误的原因。另一方面，STN依赖于线性插值，这意味着每个采样点的梯度对于两个最近的像素而言都是非零的。

 

结论

 

注意力机制扩展了神经网络的能力：它们能接近更复杂的函数，或者更直观地说，它们可以专注于输入的特定部分。它们使自然语言基准测试的性能得到改进，以及赋予图像字幕、记忆网络和神经程序的全新能力。