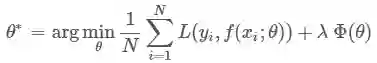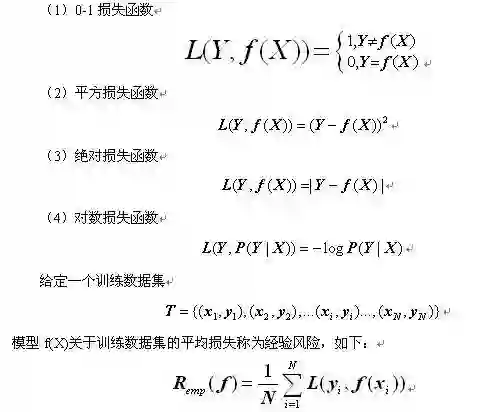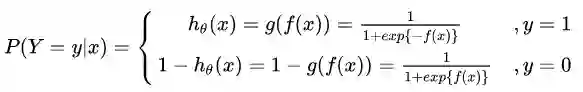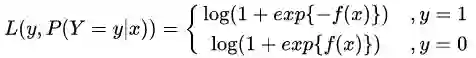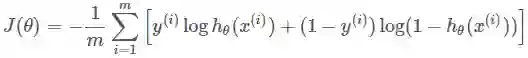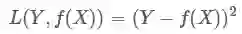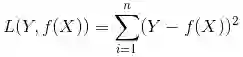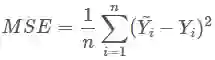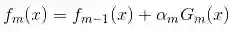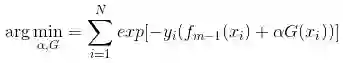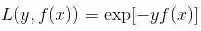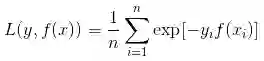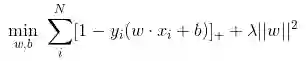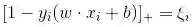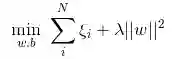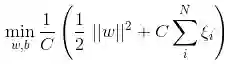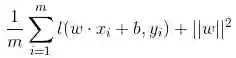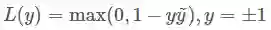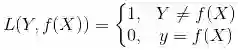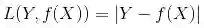详解常见的损失函数

对于给定的输入X，由f(X)给出相应的输出Y，这个输出的预测值f(X)与真实值Y可能一致也可能不一致（要知道，有时损失或误差是不可避免的），用一个损失函数来度量预测错误的程度。损失函数记为L(Y, f(X))，用来估量你模型的预测值f(x)与真实值Y的不一致程度。

损失函数越小，模型的鲁棒性就越好。损失函数是经验风险函数的核心部分，也是结构风险函数重要组成部分。模型的结构风险函数包括了经验风险项和正则项，通常可以表示成如下式子：

其中，前面的均值函数表示的是经验风险函数，L代表的是损失函数，后面的Φ是正则化项（regularizer）或者叫惩罚项（penalty term），它可以是L1，也可以是L2，或者其他的正则函数。整个式子表示的意思是找到使目标函数最小时的θ值。下面主要列出几种常见的损失函数。

常用的损失函数有以下几种（基本引用自《统计学习方法》）：

接下来，我们来重点看下 下面几种损失函数。

一、log对数损失函数（逻辑回归）

有些人可能觉得逻辑回归的损失函数就是平方损失，其实并不是。平方损失函数可以通过线性回归在假设样本是高斯分布的条件下推导得到，而逻辑回归得到的并不是平方损失。在逻辑回归的推导中，它假设样本服从伯努利分布（0-1分布），然后求得满足该分布的似然函数，接着取对数求极值等等。

而逻辑回归并没有求似然函数的极值，而是把极大化当做是一种思想，进而推导出它的经验风险函数为：最小化负的似然函数（即max F(y, f(x)) —> min -F(y, f(x)))。从损失函数的视角来看，它就成了log损失函数了。

log损失函数的标准形式：

L(Y,P(Y|X))=−logP(Y|X)

刚刚说到，取对数是为了方便计算极大似然估计，因为在MLE中，直接求导比较困难，所以通常都是先取对数再求导找极值点。

损失函数L(Y, P(Y|X))表达的是样本X在分类Y的情况下，使概率P(Y|X)达到最大值（换言之，就是利用已知的样本分布，找到最有可能（即最大概率）导致这种分布的参数值；或者说什么样的参数才能使我们观测到目前这组数据的概率最大）。因为log函数是单调递增的，所以logP(Y|X)也会达到最大值，因此在前面加上负号之后，最大化P(Y|X)就等价于最小化L了。

逻辑回归的P(Y=y|x)表达式如下（为了将类别标签y统一为1和0，下面将表达式分开表示）：

将它带入到上式，通过推导可以得到logistic的损失函数表达式，如下：

逻辑回归最后得到的目标式子如下：

二、平方损失函数（最小二乘法, Ordinary Least Squares ）

最小二乘法是线性回归的一种，OLS将问题转化成了一个凸优化问题。在线性回归中，它假设样本和噪声都服从高斯分布（为什么假设成高斯分布呢？其实这里隐藏了一个小知识点，就是中心极限定理，可以参考：https://blog.csdn.net/v_july_v/article/details/8308762），最后通过极大似然估计（MLE）可以推导出最小二乘式子。最小二乘的基本原则是：最优拟合直线应该是使各点到回归直线的距离和最小的直线，即平方和最小。

换言之，OLS是基于距离的，而这个距离就是我们用的最多的欧几里得距离。为什么它会选择使用欧式距离作为误差度量呢（即Mean squared error， MSE），主要有以下几个原因：

简单，计算方便；

欧氏距离是一种很好的相似性度量标准；

在不同的表示域变换后特征性质不变。

平方损失（Square loss）的标准形式如下：

当样本个数为n时，此时的损失函数变为：

Y-f(X)表示的是残差，整个式子表示的是残差的平方和，而我们的目的就是最小化这个目标函数值（注：该式子未加入正则项），也就是最小化残差的平方和（residual sum of squares，RSS）。

而在实际应用中，通常会使用均方差（MSE）作为一项衡量指标，公式如下：

上面提到了线性回归，这里额外补充一句，我们通常说的线性有两种情况，一种是因变量y是自变量x的线性函数，一种是因变量y是参数αα的线性函数。在机器学习中，通常指的都是后一种情况。

三、指数损失函数（Adaboost）

学过Adaboost算法的人都知道，它是前向分步加法算法的特例，是一个加和模型，损失函数就是指数函数。在Adaboost中，经过m此迭代之后，可以得到fm(x)fm(x):

Adaboost每次迭代时的目的是为了找到最小化下列式子时的参数α和G：

而指数损失函数(exp-loss）的标准形式如下

可以看出，Adaboost的目标式子就是指数损失，在给定n个样本的情况下，Adaboost的损失函数为：

关于Adaboost的推导，可以参考：https://blog.csdn.net/v_july_v/article/details/40718799

四、Hinge损失函数（SVM）

在机器学习算法中，hinge损失函数和SVM是息息相关的。在线性支持向量机中，最优化问题可以等价于下列式子：

 

下面来对式子做个变形，令：

于是，原式就变成了：

如若取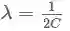，式子就可以表示成：

可以看出，该式子与下式非常相似：

前半部分中的ll就是hinge损失函数，而后面相当于L2正则项。

Hinge 损失函数的标准形式

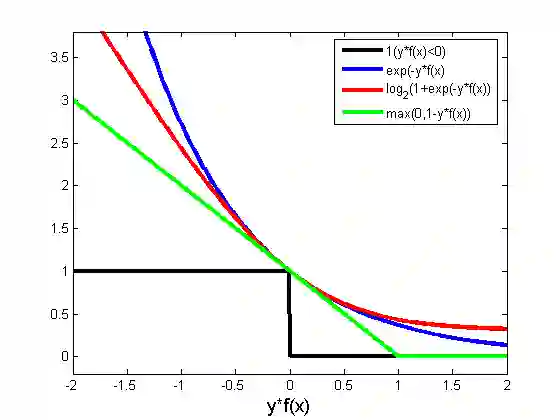
可以看出，当|y|>=1时，L(y)=0。

补充一下：在libsvm中一共有4中核函数可以选择，对应的是-t参数分别是：

0-线性核；

1-多项式核；

2-RBF核；

3-sigmoid核。

如此，SVM有第二种理解，即最优化+损失最小，或如@夏粉_百度所说“可从损失函数和优化算法角度看SVM，boosting，LR等算法，可能会有不同收获”。

关于SVM的更多理解请参考：支持向量机通俗导论（理解SVM的三层境界），链接：http://blog.csdn.net/v_july_v/article/details/7624837

五、其它损失函数

除了以上这几种损失函数，常用的还有：

0-1损失函数

绝对值损失函数

以下是几种损失函数的可视化图像：

参考文献：

http://www.csuldw.com/2016/03/26/2016-03-26-loss-function/

题目来源：

七月在线官网（https://www.julyedu.com/）——面试题库——面试大题——机器学习 第26题。

机器学习中所有的算法都需要最大化或最小化一个函数，这个函数被称为“目标函数”。其中，我们一般把最小化的一类函数，称为“损失函数”。它能根据预测结果，衡量出模型预测能力的好坏。“损失函数”是机器学习优化中至关重要的一部分。

为了帮助大家系统地学习机器学习课程的相关知识，我们特意推出了机器学习集训营系列课程。迄今为止，「机器学习集训营」已经举办了四期，每一期都涌现出了不少优秀offer，特别是上一期很多同学从Java、Android、iOS等传统IT行业成功转行转型转岗AI拿到年薪三四十万，部分甚至超过四十万拿到五十万。

本第五期，在第四期的基础上，除了继续维持“入学测评、直播答疑、布置作业、阶段考试、毕业考核、一对一批改、线上线下结合、CPU&GPU双云平台、组织比赛、面试辅导、就业推荐”十一位一体的教学模式，本期特地推出机器学习工程师联合认证。且线下在北京、上海、深圳、广州、杭州、沈阳、济南、郑州、成都的基础上，新增武汉、西安两个线下点，十一城同步开营。

此外，本期依然沿用前四期线上线下相结合的授课方式，加强项目实训的同时引入线下BAT专家面对面、手把手的教学方式；突出BAT级工业项目实战辅导 + 一对一面试求职辅导，并提供一年GPU云实验平台免费使用，精讲面试考点。让每一位学员不用再为遇到问题没人解答，缺乏实战经验以及简历上没有项目经验，面试屡屡遭拒而发愁。

本期限150个名额，历时3个月，10多个BAT级工业项目，保障每一位学员所学更多、效率更高、收获更大。

机器学习集训营 第五期 课程详情可点击文末“阅读原文”进行查看，或者加微信客服：julyedukefu_02进行咨询。