什么是扩散模型？谷歌大脑Calvin Luo最新《扩散模型理解》，带你对基于评分与基于能量的扩散模型的统一视角数学理解

给定目标分布中的观察样本x，生成模型的目标是学习为其真实的数据分布p(x)建模。一旦学习，我们可以从我们的近似模型任意生成新的样本。此外，在一些公式下，我们能够使用学习的模型来评估观察或抽样数据的可能性。在目前的文献中有几个著名的方向，我们将只在较高的水平上简要介绍。生成对抗网络(GANs)模拟了一个复杂分布的抽样过程，它是通过对抗的方式学习的。另一类生成模型被称为“基于似然的”，它试图学习一个模型，该模型为观察到的数据样本分配高可能性。这包括自回归模型、标准化流和变分自动编码器(VAEs)。另一种类似的方法是基于能量的建模，在这种方法中，分布被学习为任意灵活的能量函数，然后被归一化。基于评分的生成模型是高度相关的; 他们不是学习建立能量函数本身的模型，而是将基于能量的模型的评分作为神经网络来学习。在这项工作中，我们探索和回顾了扩散模型，正如我们将展示的，有基于似然和基于评分的解释。我们以令人痛苦的细节展示了这些模型背后的数学，目的是让任何人都可以跟随并理解扩散模型是什么以及它们如何工作。

ELBO, VAE, 和 Hierarchical VAE

对于许多模态，我们可以认为我们观察到的数据是由一个相关的看不见的潜在变量表示或产生的，我们可以用随机变量z表示。表达这一想法的最佳直觉是通过柏拉图的洞穴寓言。在这个寓言中，一群人一生都被锁在一个洞穴里，只能看到投射在他们面前墙上的二维阴影，这些阴影是由在火前经过的看不见的三维物体产生的。对这些人来说，他们所观察到的一切实际上都是由他们永远无法看到的高维抽象概念所决定的。

类似地，我们在现实世界中遇到的对象也可能是一些更高层次表征的函数;例如，这样的表示可以封装诸如颜色、大小、形状等抽象属性。那么，我们所观察到的就可以被解释为三维投影或这些抽象概念的实例化，就像穴居人所观察到的其实是三维物体的二维投影一样。虽然穴居人永远看不到(甚至完全理解)隐藏的物体，但他们仍然可以对它们进行推理和推断;以类似的方式，我们可以近似描述我们观察到的数据的潜在表示。

柏拉图的寓言阐述了潜在变量背后的想法，作为潜在的不可观察的表征来决定观察，这个类比的一个警告是，在生成建模中，我们通常寻求学习低维的潜在表征，而不是高维的。这是因为如果没有强大的先验，试图学习比观察更高维度的表示是徒劳的。另一方面，学习低维潜势也可以被视为一种压缩形式，并可能揭示描述观察结果的语义有意义的结构。

在默认的变分自动编码器(VAE)[1]的公式中，我们直接最大化了ELBO。这种方法是变分的，因为我们在一个由φ参数化的潜在后验分布家族中优化最佳的qφ(z|x)。它之所以被称为自动编码器，是因为它让人想起了传统的自动编码器模型，在传统的自动编码器模型中，输入数据经过中间瓶颈表示步骤后被训练成预测自己。为了明确这种联系，让我们进一步分析ELBO术语:

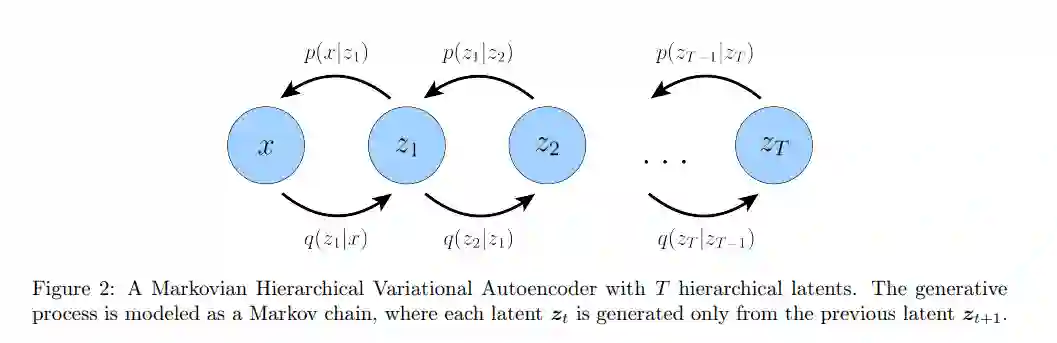
分层变分自动编码器(HVAE)[2,3]是扩展到潜变量的多重层次的一种推广。在这个公式下，潜在变量本身被解释为由其他更高级、更抽象的潜在变量生成。直观地说，就像我们把三维被观察的物体看成是由更高层次的抽象潜伏体产生的一样，柏拉图洞穴里的人把三维物体看成是产生二维观测的潜伏体。因此，从柏拉图的洞穴居民的角度来看，他们的观察可以被视为一个深度2(或更多)的潜在层次模型。

变分扩散模型 Variational Diffusion Models

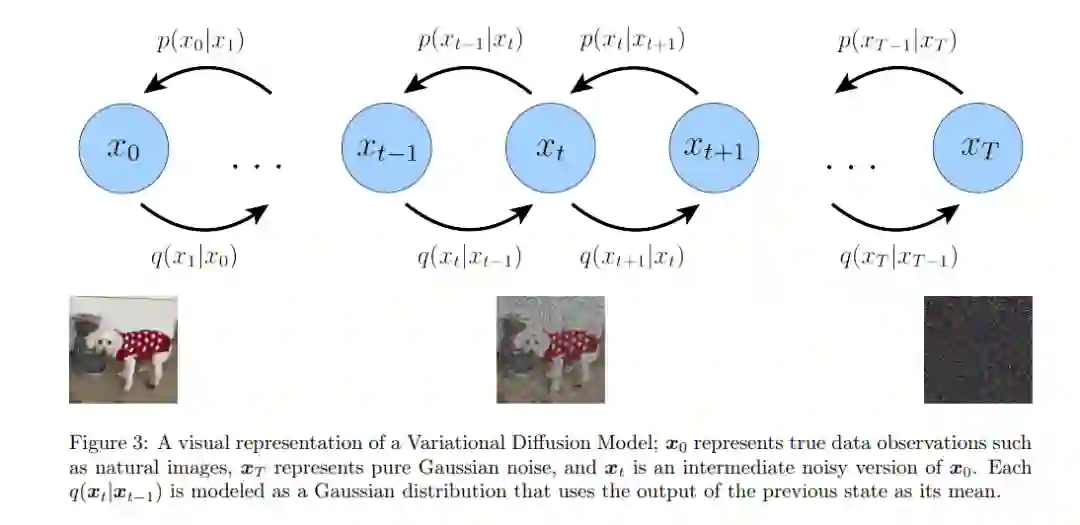
最简单的方法是把变分扩散模型(VDM)[4,5,6]简单地看作是一个马尔可夫层次变分自编码器，有三个关键的限制条件: * 潜在维度与数据维度完全相等 * 不学习每个时步的潜在编码器的结构;它被预先定义为线性高斯模型。换句话说，它是一个以前一个时间步长的输出为中心的高斯分布 * 潜在编码器的高斯参数随时间变化，在最终时间步T的分布是标准高斯

结论

请允许我们总结一下我们在探索过程中的发现。首先，我们推导了变分扩散模型作为马尔可夫层次变分自动编码器的特殊情况，其中三个关键假设使ELBO的可跟踪计算和可扩展优化成为可能。然后，我们证明优化VDM可以归结为学习一个神经网络来预测以下三个潜在目标之一:来自任意噪声化的原始源图像，来自任意噪声化图像的原始源噪声，或在任意噪声水平上的噪声化图像的评分函数。然后，我们深入研究评分函数的含义，并明确地将其与基于评分的生成模型的视角联系起来。最后，我们将介绍如何使用扩散模型学习条件分布。

总之，扩散模型表现出了生成模型不可思议的能力;事实上，它们为目前最先进的基于文本条件的图像生成模型(如Imagen和DALL-E 2)提供了动力。此外，建立这些模型的数学运算非常优雅**。但是，仍然有一些缺点需要考虑:
这不太可能是我们作为人类自然建模和生成数据的方式;我们不生成样本作为我们迭代去噪的随机噪声。
VDM不会产生可解释的潜量。VAE算法希望通过编码器的优化来获得一个结构化的潜在空间，而在VDM中，编码器在每个时间步长的位置都是线性高斯模型，不能灵活地优化。因此，中间潜伏被限制为原始输入的噪声版本。
潜势被限制在与原始输入相同的维度，进一步阻碍了学习有意义的压缩潜势结构的努力。
采样是一个昂贵的过程，因为在两种配方下必须运行多个去噪步骤。回想一下，其中一个限制是选择足够多的时间步T，以确保最终潜伏是完全高斯噪声;在采样期间，我们必须遍历所有这些时间步来生成一个样本。

最后，扩散模型的成功凸显了层次式VAE模型作为生成模型的力量。我们已经证明，当我们推广到无限潜在层次时，即使编码器是微不足道的，潜在维是固定的，并且假设马尔可夫跃迁，我们仍然能够学习强大的数据模型。这表明，在一般的深度HVAEs情况下，可以获得进一步的性能提高，其中复杂的编码器和语义有意义的潜在空间可以学习。