激活函数还是有一点意思的！

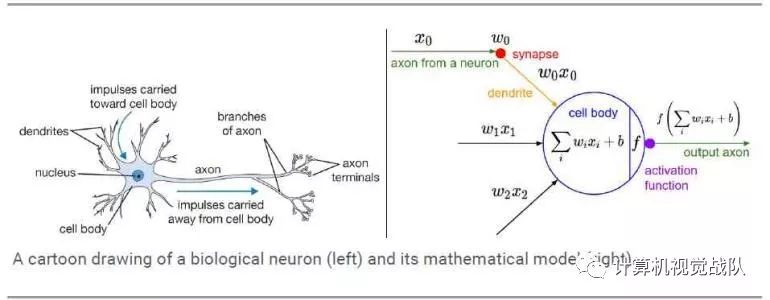
激活函数（Activation functions）对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如在神经元中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数。

引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。

为什么要用激活函数？

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少深，输出都是输入的线性组合，这种情况就是最原始的感知机。

如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。一般激活函数有如下一些性质：

• 非线性： 

  当激活函数是线性的，两层的神经网络就可以基本上逼近所有的函数。但如果激活函数是恒等激活函数的时候，即f(x)=x，就不满足这个性质，而且如果MLP使用的是恒等激活函数，那么其实整个网络跟单层神经网络是等价的；

• 可微性： 
  当优化方法是基于梯度的时候，就体现了该性质；

• 单调性： 
  当激活函数是单调的时候，单层网络能够保证是凸函数；

• f(x)≈x： 
  当激活函数满足这个性质的时候，如果参数的初始化是随机的较小值，那么神经网络的训练将会很高效；如果不满足这个性质，那么就需要详细地去设置初始值；

• 输出值的范围： 
  当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限的时候，模型的训练会更加高效，不过在这种情况小，一般需要更小的Learning Rate。

那接下来，我们就开始讲讲激活函数。

ReLU

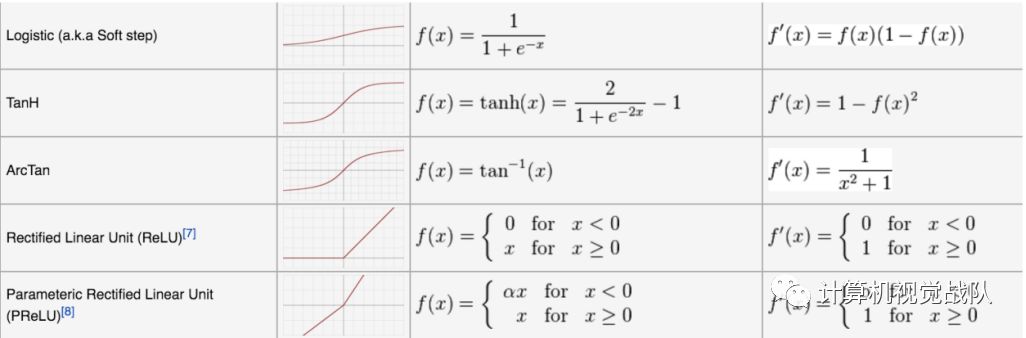
今天主要说的就是ReLU激活函数，其全名叫修正线性单元(Rectified linear unit）。

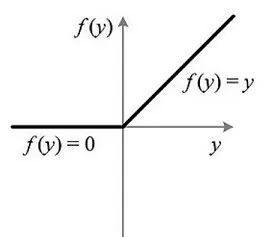
f(x)=max(0,x)

优点： 
使用 ReLU得到的SGD的收敛速度会比 sigmoid/tanh 快。这是因为它是linear，而且ReLU只需要一个阈值就可以得到激活值，不用去计算复杂的运算。

缺点： 

训练过程该函数不适应较大梯度输入，因为在参数更新以后，ReLU的神经元不会再有激活的功能，导致梯度永远都是零。

细说ReLU

上图就是ReLU的可视化图，其实ReLU还是可以将其归为线性函数，如果更加准确的话，那就是分段线性函数。如果输入的值小于等于0的时候，输出全部给予0值，而大于0输入，就按照正常线性处理。

该处理形式被称为单侧抑制机制，这种机制可就厉害啦！

• 第一，采用sigmoid、Tanh等激活函数时，计算激活函数时计算量教大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多；

• 第二，对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练；

• 第三，ReLu会使一部分神经元的输出为0，这样就使网络稀疏，且减少了参数的相互依存关系，缓解了过拟合问题的发生。

为啥ReLU的激活函数形式要这样书写，不可以镜面反转之类的吗？不又成新的一种激活函数？

其实很简单，这里激活函数主要核心是单侧抑制，所以不管你是在哪个象限内进行抑制操作，最后目的都是一样。无论是镜面反转还是180度翻转，最终神经元的输出也只是相当于加上了一个常数项系数，并不影响模型的训练结果。

ReLU激活函数还有一大好处就是稀疏了参数，这个作用对于深度网络来说就是神来之笔。稀疏有何作用呢？接下来我引用偏执的眸一段比如，简单太形象的解释了这个问题。

🌰

当看名侦探柯南的时候，我们可以根据故事情节进行思考和推理，这时用到的是我们的大脑左半球；而当看蒙面唱将时，我们可以跟着歌手一起哼唱，这时用到的则是我们的右半球。左半球侧重理性思维，而右半球侧重感性思维。也就是说，当我们在进行运算或者欣赏时，都会有一部分神经元处于激活或是抑制状态，可以说是各司其职。再比如，生病了去医院看病，检查报告里面上百项指标，但跟病情相关的通常只有那么几个。与之类似，当训练一个深度分类模型的时候，和目标相关的特征往往也就那么几个，因此通过ReLU实现稀疏后的模型能够更好地挖掘相关特征，拟合训练数据。

实验比较

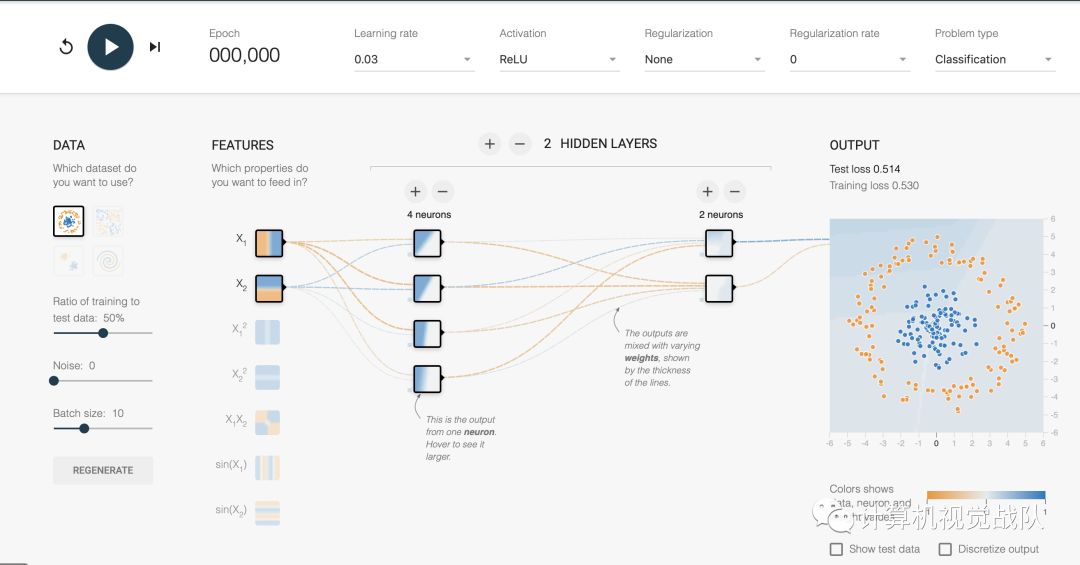
本次试验在playground界面进行实验，想必很多同学对这个小平台有很深入的理解。以2分类解释：

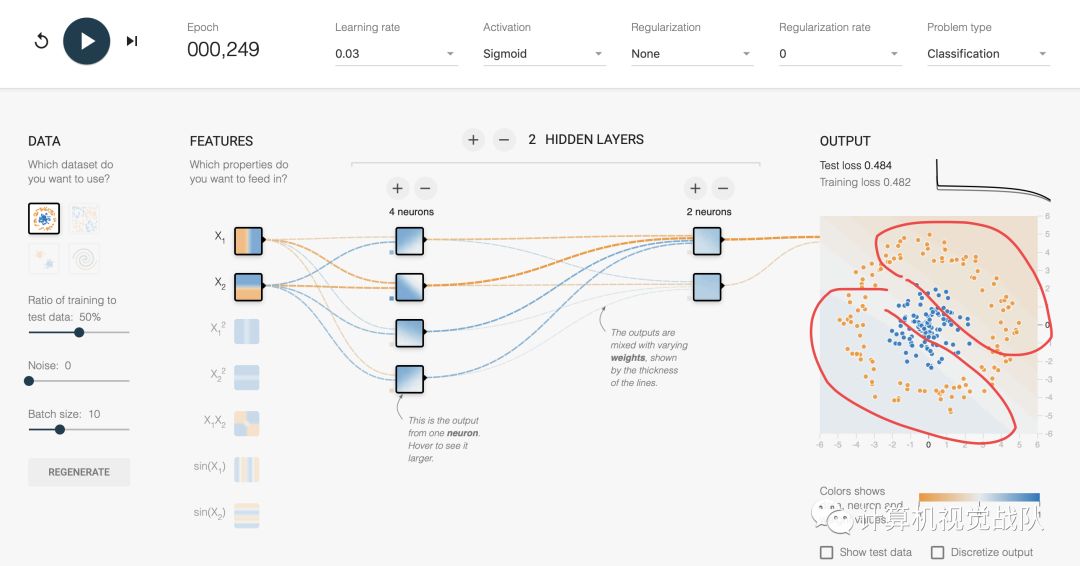
第一种情况：使用Sigmoid函数，进行训练：

当运行了部分时间后，发现分界面依然模糊不清，还要继续训练，如下图：

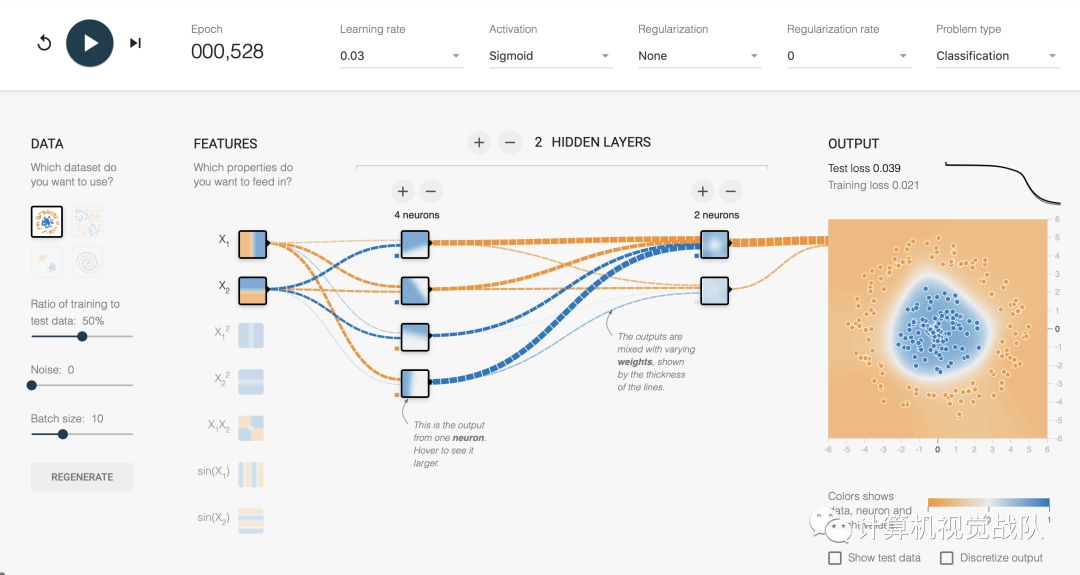
当运行了528Epoch，才全部分开，如下图：

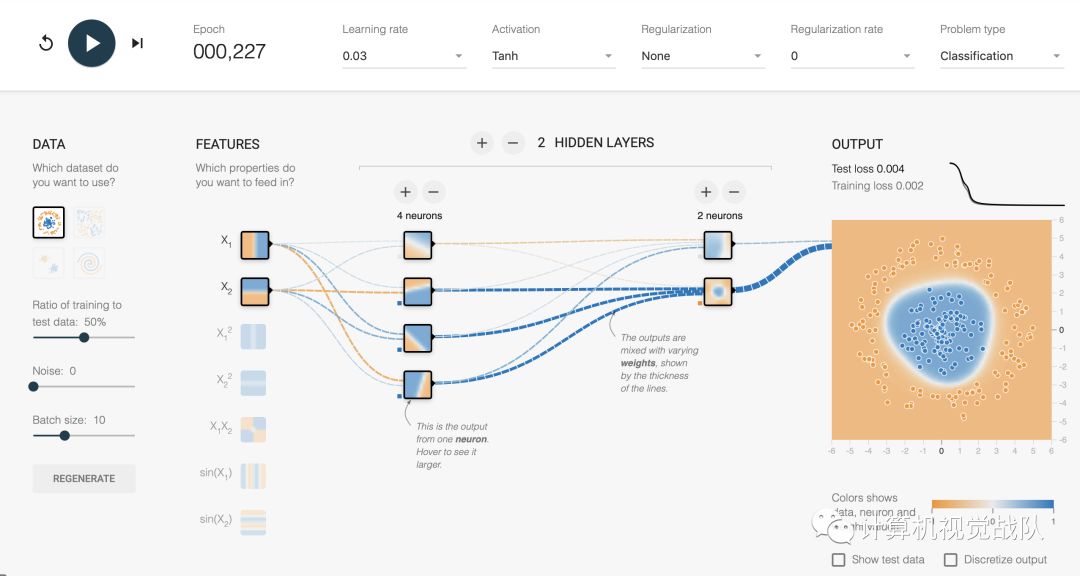
第二种情况：使用Tanh函数，进行训练：

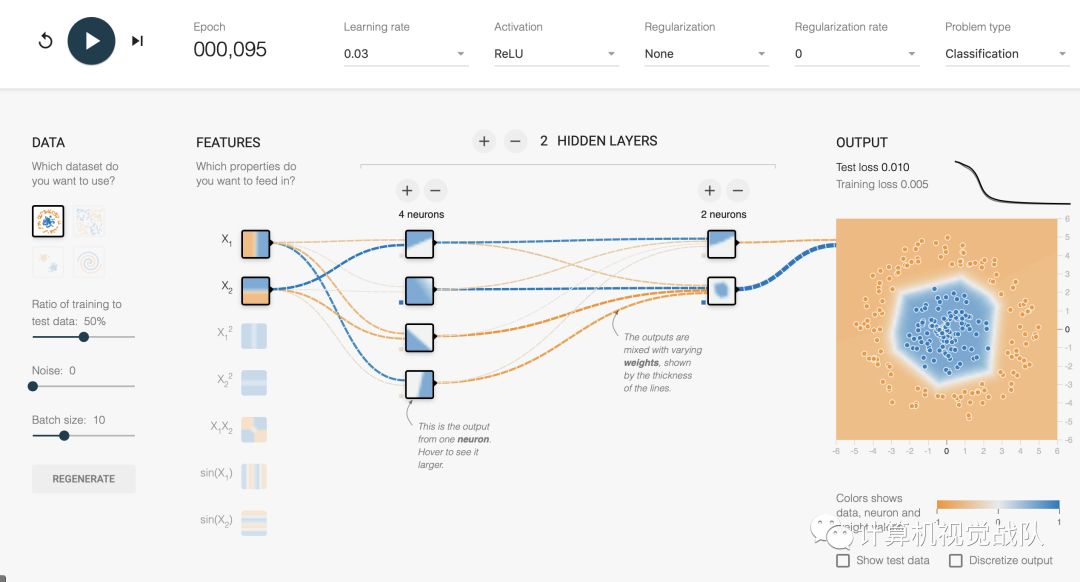
第三种情况：使用ReLU函数，进行训练：

综上，可以明显发现ReLU效果最好而且速度最快。

• 就会有同学问：为什么通常Relu比sigmoid和tanh强，有什么不同？

其实之前已经回答了，主要是因为它们gradient特性不同。sigmoid和tanh的gradient在饱和区域非常平缓，接近于0，很容易造成vanishing gradient的问题，减缓收敛速度。vanishing gradient在网络层数多的时候尤其明显，是加深网络结构的主要障碍之一。相反，Relu的gradient大多数情况下是常数，有助于解决深层网络的收敛问题。Relu的另一个优势是在生物上的合理性，它是单边的，相比sigmoid和tanh，更符合生物神经元的特征；而提出sigmoid和tanh，主要是因为它们全程可导；还有表达区间问题，sigmoid和tanh区间是0到1，或着-1到1，在表达上，尤其是输出层的表达上有优势。ReLU更容易学习优化。因为其分段线性性质，导致其前传，后传，求导都是分段线性。而传统的sigmoid函数，由于两端饱和，在传播过程中容易丢弃信息。

如果想加入我们“计算机视觉战队”，请扫二维码加入学习群。计算机视觉战队主要涉及机器学习、深度学习等领域，由来自于各校的硕博研究生组成的团队，主要致力于人脸检测、人脸识别，多目标检测、目标跟踪、图像分割等研究方向。

我们开创一段时间的“计算机视觉协会”知识星球，也得到很多同学的认可，我们定时会推送实践型内容与大家分享，在星球里的同学可以随时提问，随时提需求，我们都会及时给予回复及给出对应的答复。

微信学习讨论群也可以加入，我们会第一时间在该些群里预告！