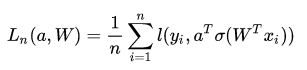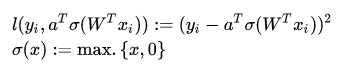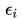神经网络的损失函数为什么是非凸的?

加入极市专业CV交流群，与6000+来自腾讯，华为，百度，北大，清华，中科院等名企名校视觉开发者互动交流！更有机会与李开复老师等大牛群内互动！

同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流。关注 极市平台 公众号 ，回复 加群，立刻申请入群~

作者：覃含章

https://www.zhihu.com/question/265516791/answer/769005628

来源：知乎，已获作者授权转载，禁止二次转载。

简单说下这个问题吧。

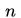
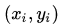
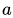
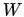
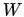
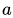
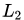
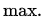
考虑最简单的一类神经网络，只有一个隐层、和输入输出层的网络。也就是说给定组样本，我们网络的经验损失函数可以写成：

、就是我们要优化的权重：代表输入层到隐层的权重， 代表隐层到输出层的权重。这里我们取 损失函数和ReLU作为我们的激活函数。即上式中（用 代表对向量每一个元素取max）

注意到虽然像取平方，ReLU激活函数 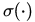，求内积这些“函数”单独来看都是凸的，但他们这么一复合之后就不一定是凸的了。一些常见的判断凸函数的方法请见：

怎么判断一个优化问题是凸优化还是非凸优化？

（文章链接：https://www.zhihu.com/question/334515180/answer/748981244）

为了方便说明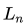这个函数是非凸的，我们需要一个经典引理：一个高维凸函数可以等价于无数个一维凸函数的叠加。

一个（高维）函数是凸的，当且仅当把这个函数限制到任意直线上它在定义域上仍然是凸的。这是凸分析里很基本的一个定理，不熟悉的同学不妨尝试用定义来证明它。

更正式的来说，

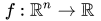
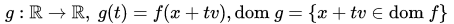
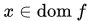
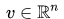
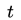
引理：是凸的，当且仅当

对任意，，关于是凸的。

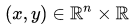
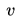
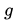
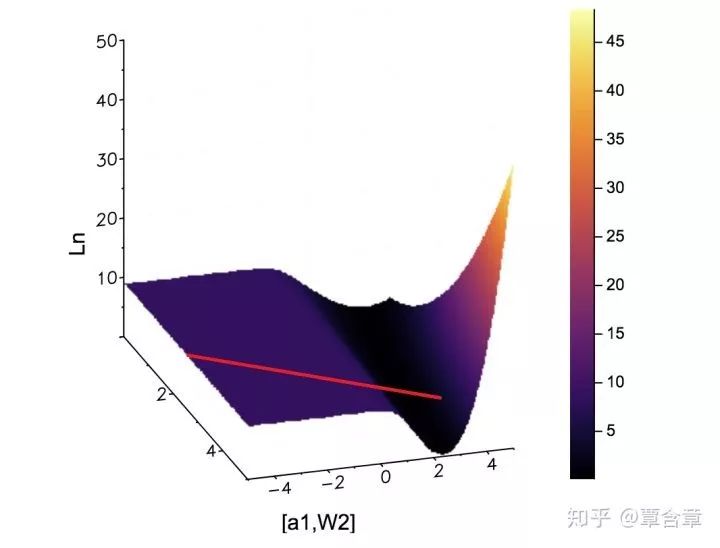
反过来也就是说，只要我们找到一点，和一个“方向” ，使得这个函数非凸就可以了！ 回顾一维凸函数的定义，这就是说在这个方向上找到两个点，他们平均的函数值比他们平均值上的函数值要低就行了！

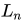
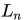
最后就是轻松愉快的画图举反例环节。这边为了说明方便，取参数空间为四维的  。不过这种思路其实对任意维度的  都成立，只要画图的时候任选两个维度就好（把其它维度的值固定住）。

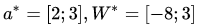
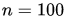
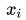
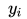
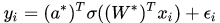
这里我们取真实的  。然后均匀随机地生成  个 （二维的[0,1]均匀随机向量）， 就用 生成，

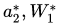
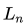
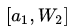
 是[0,0.5]的均匀随机数（这样图像看起来会比较规整）。我们固定住 ，画出采样出来的  在 上的图像：



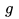
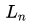
如上红线，我们可以很轻松的找到一条使 “非凸”的线，因此证明完毕： 是非凸的。

这个本质上就是 @陈泰红 （https://www.zhihu.com/people/chenhong007/activities）答案中提到Goodfellow在Quora说的思路：“plot a cross-section of the function and look at it”，而它的正确性就是这边的引理所保证的。注意到这边如果你要用求导大法是不太容易的，因为隐层套的是ReLU激活函数，只能求次微分，看起来会稍微麻烦一些。

-End-

*延伸阅读

• 40万现金大奖+免费算力+英特尔神经棒，极市开发者榜单邀你来战！

• 深度学习的这些坑你都遇到过吗？神经网络 11 大常见陷阱及应对方法
  

• 真正的神经网络，敢于不学习权重
  

添加极市小助手微信（ID : cv-mart），备注：研究方向-姓名-学校/公司-城市（如：目标检测-小极-北大-深圳），即可申请加入目标检测、目标跟踪、人脸、工业检测、医学影像、三维&SLAM、图像分割等极市技术交流群，更有每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流，一起来让思想之光照的更远吧~

△长按添加极市小助手

△长按关注极市平台

觉得有用麻烦给个在看啦~