The strength of a simplex is the key to a continuous isometry classification of Euclidean clouds of unlabelled points

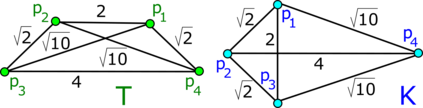
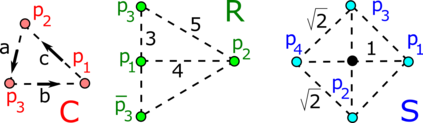
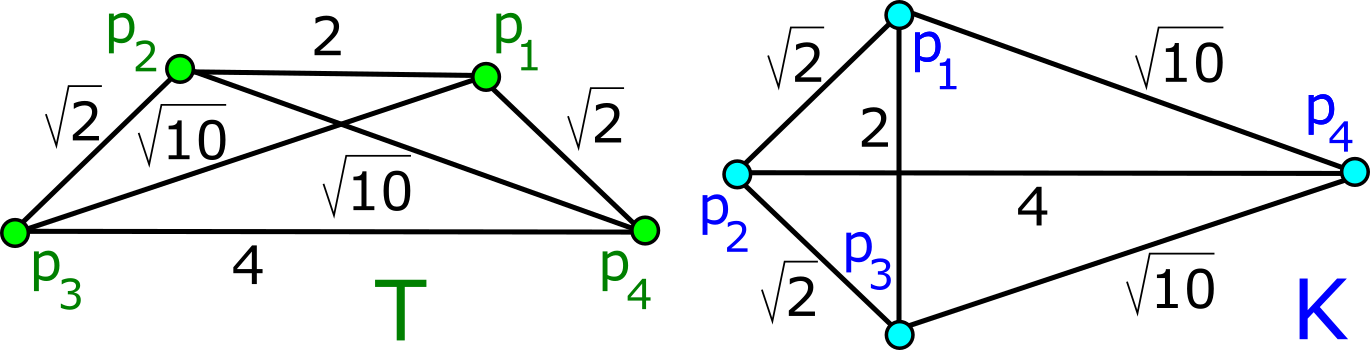
This paper solves the continuous classification problem for finite clouds of unlabelled points under Euclidean isometry. The Lipschitz continuity of required invariants in a suitable metric under perturbations of points is motivated by the inevitable noise in measurements of real objects. The best solved case of this isometry classification is known as the SSS theorem in school geometry saying that any triangle up to congruence (isometry in the plane) has a continuous complete invariant of three side lengths. However, there is no easy extension of the SSS theorem even to four points in the plane partially due to a 4-parameter family of 4-point clouds that have the same six pairwise distances. The computational time of most past metrics that are invariant under isometry was exponential in the size of the input. The final obstacle was the discontinuity of previous invariants at singular configurations, for example, when a triangle degenerates to a straight line. All the challenges above are now resolved by the Simplexwise Centred Distributions that combine inter-point distances of a given cloud with the new strength of a simplex that finally guarantees the Lipschitz continuity. The computational times of new invariants and metrics are polynomial in the number of points for a fixed Euclidean dimension.