【ICML2020】持续图神经网络，Continuous Graph Neural Networks

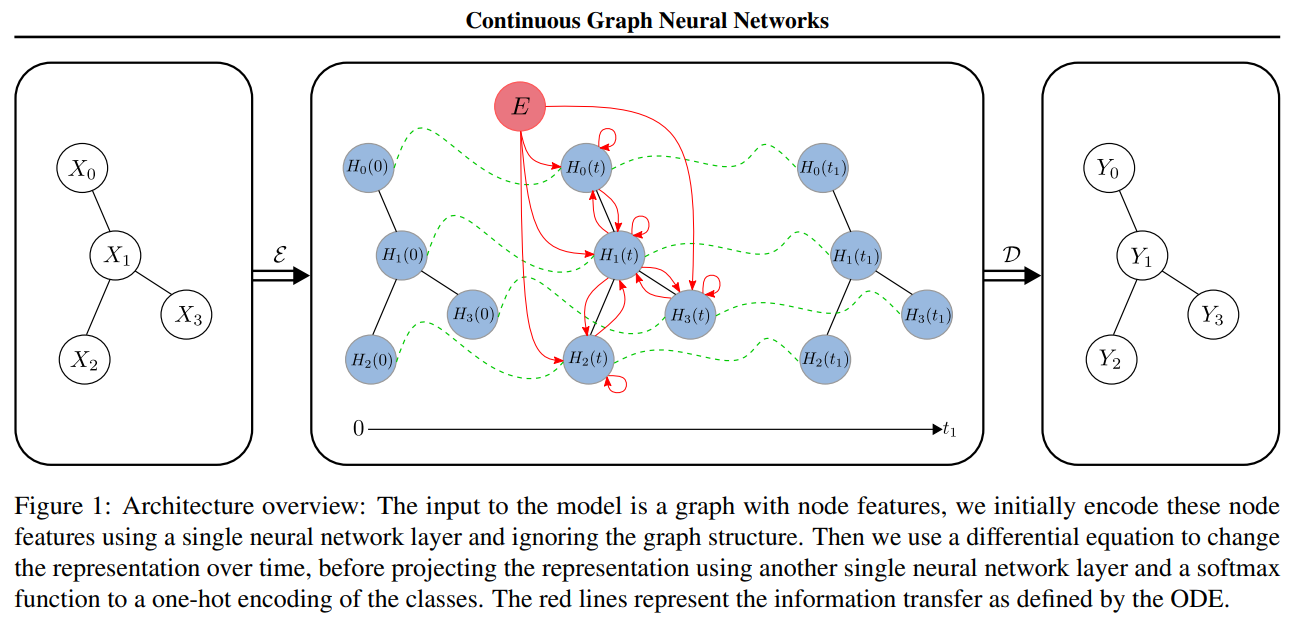
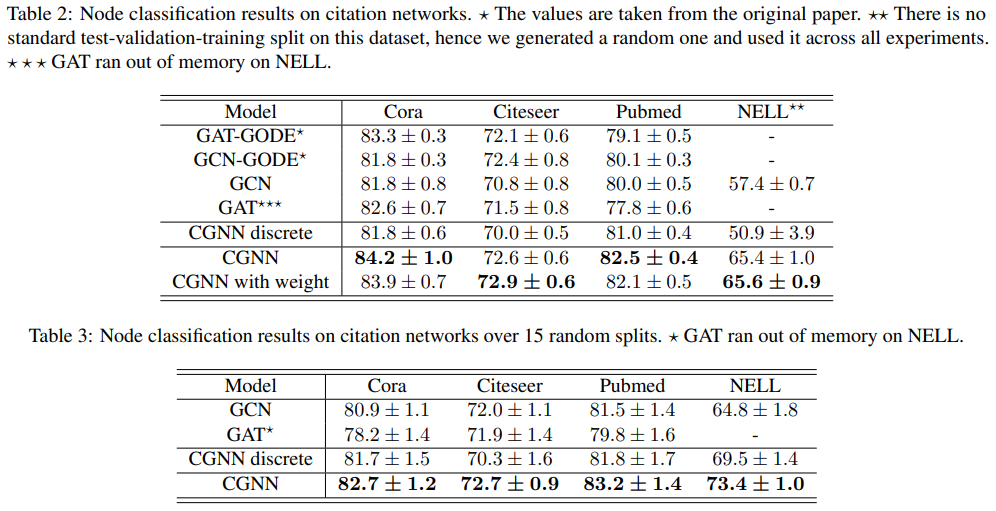
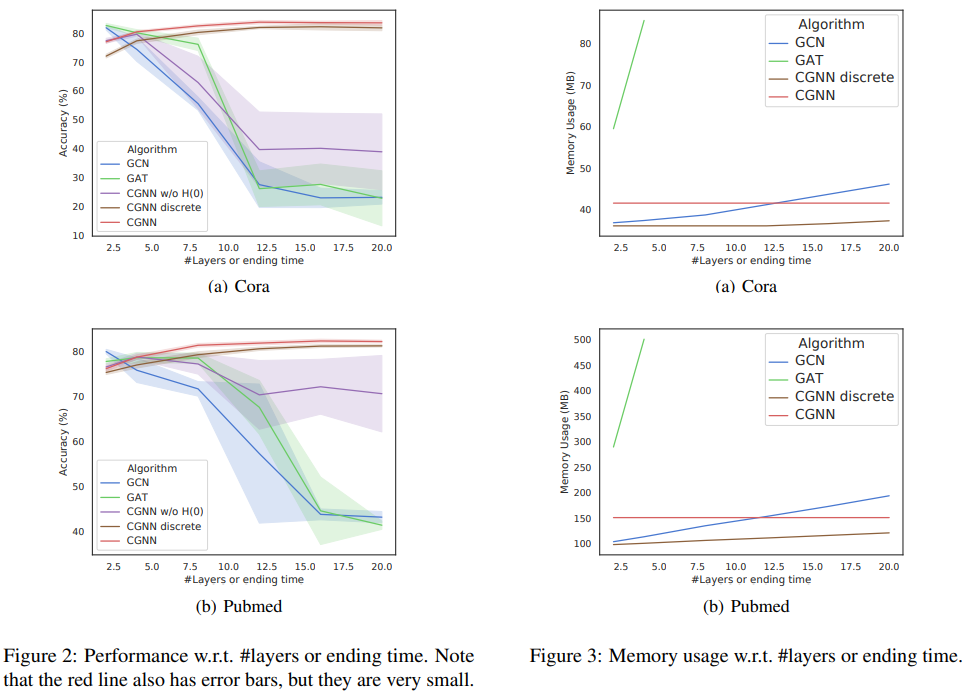
题目： Continuous Graph Neural Networks

摘要：

本文建立了图神经网络与传统动力系统之间的联系。我们提出了持续图神经网络(CGNN)，它将现有的图神经网络与离散动力学进行了一般化，因为它们可以被视为一种特定的离散化方案。关键思想是如何表征节点表示的连续动力学，即关于时间的节点表示的导数。受现有的基于扩散的图方法(如社交网络上的PageRank和流行模型)的启发，我们将导数定义为当前节点表示、邻节点表示和节点初始值的组合。我们提出并分析了两种可能的动态图，包括节点表示的每个维度(又名特征通道)各自改变或相互作用的理论证明。所提出的连续图神经网络在过度平滑方面具有很强的鲁棒性，因此允许我们构建更深层次的网络，进而能够捕获节点之间的长期依赖关系。在节点分类任务上的实验结果证明了我们提出的方法在和基线对比的有效性。

介绍

图神经网络(GNNs)由于其在节点分类等多种应用中的简单性和有效性而受到越来越多的关注;、链接预测、化学性质预测、自然语言理解。GNN的基本思想是设计多个图传播层，通过聚合邻近节点的节点表示和节点本身的表示，迭代地更新每个节点表示。在实践中，对于大多数任务，几层(两层或三层)通常就足够了，更多的层可能导致较差的性能。

改进GNNs的一个关键途径是能够建立更深层次的网络，以了解数据和输出标签之间更复杂的关系。GCN传播层平滑了节点表示，即图中相邻的节点变得更加相似。当我们堆叠越来越多的层时，这会导致过度平滑，这意味着节点表示收敛到相同的值，从而导致性能下降。因此，重要的是缓解节点过平滑效应，即节点表示收敛到相同的值。

此外，对于提高我们对GNN的理论理解，使我们能够从图结构中描述我们可以学到的信号，这是至关重要的。最近关于理解GCN的工作(Oono和Suzuki, 2020)认为GCN是由离散层定义的离散动力系统。此外，Chen等人(2018)证明了使用离散层并不是构建神经网络的唯一视角。他们指出，带有剩余连接的离散层可以看作是连续ODE的离散化。他们表明，这种方法具有更高的记忆效率，并且能够更平滑地建模隐藏层的动态。

我们利用基于扩散方法的连续视角提出了一种新的传播方案，我们使用来自常微分方程(即连续动力系统)的工具进行分析。事实上，我们能够解释我们的模型学习了什么表示，以及为什么它不会遭受在GNNs中常见的过度平滑问题。允许我们建立更深层次的网络，也就是说我们的模型在时间价值上运行良好。恢复过平滑的关键因素是在连续设置中使用了最初在PageRank中提出的原始分布。直观上，重新开始分布有助于不忘记邻接矩阵的低幂次信息，从而使模型收敛到有意义的平稳分布。

本文的主要贡献是:

• 基于PageRank和扩散方法，提出了两个连续递增模型容量的ODEs;
• 我们从理论上分析了我们的层学习的表示，并表明当t → ∞我们的方法接近一个稳定的不动点，它捕获图结构和原始的节点特征。因为我们在t→∞时是稳定的，我们的网络可以有无限多个“层”，并且能够学习远程依赖关系;
• 我们证明了我们的模型的记忆是高效的，并且对t的选择是具有鲁棒性的。除此之外，我们进一步证明了在节点分类任务上，我们的模型能够比许多现有的最先进的方法表现更好。