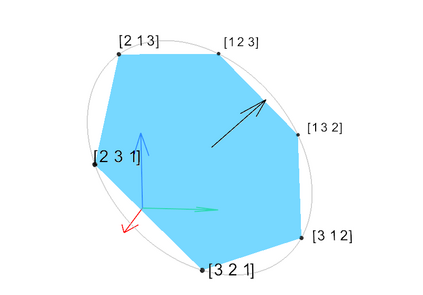
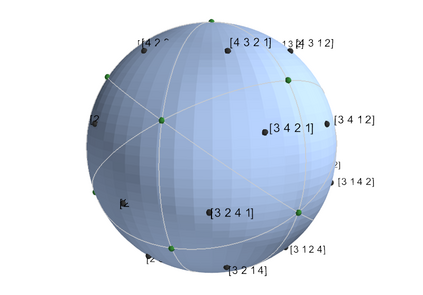
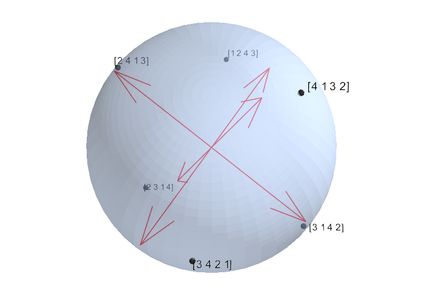
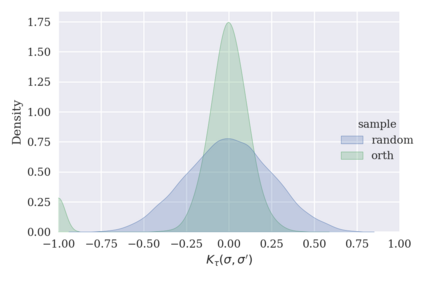
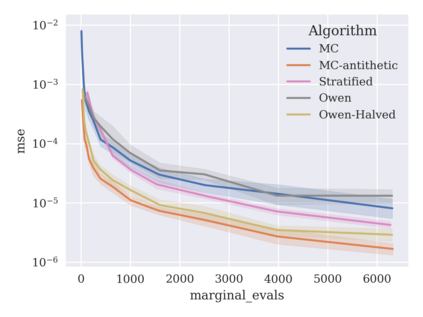
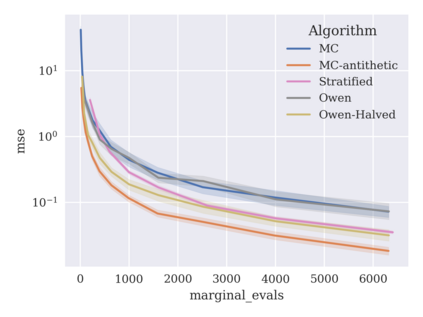
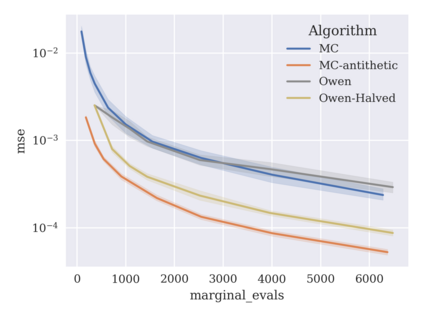
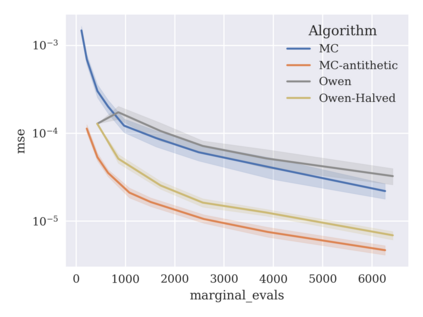
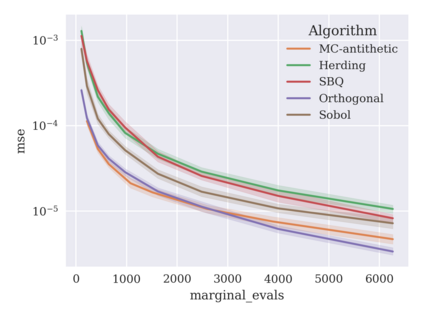
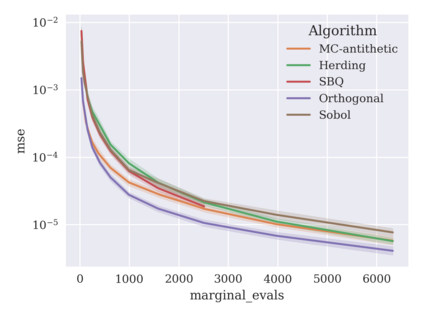
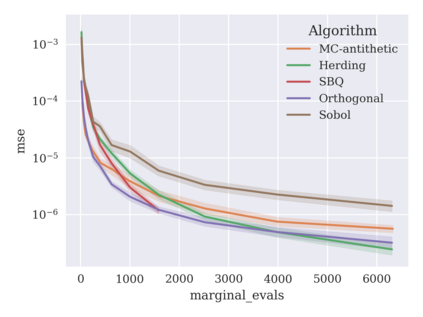
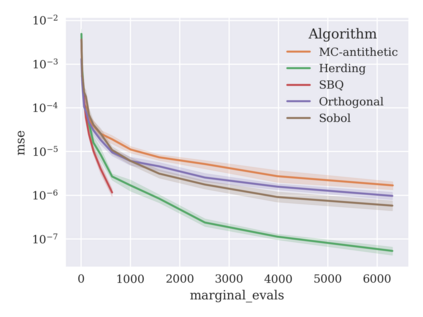
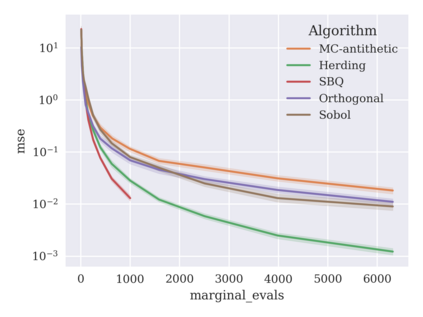
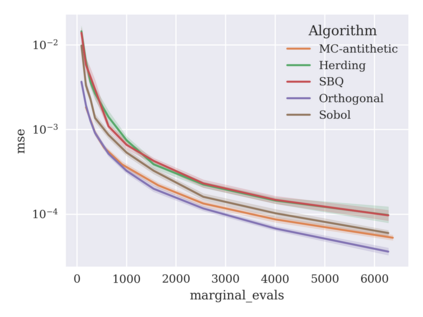
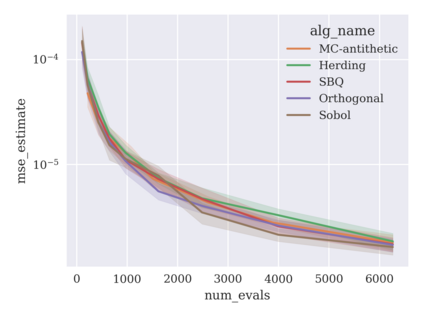
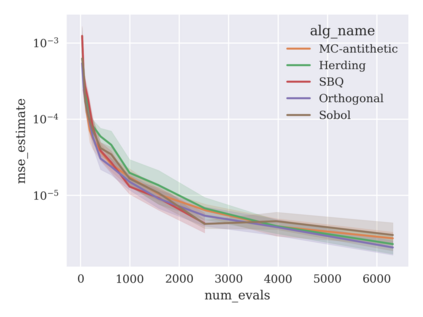
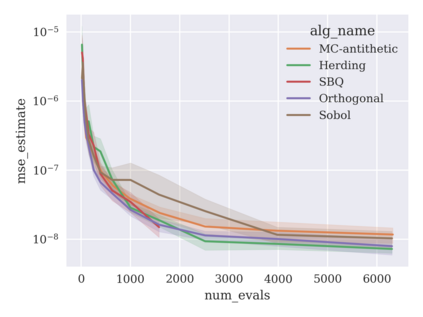
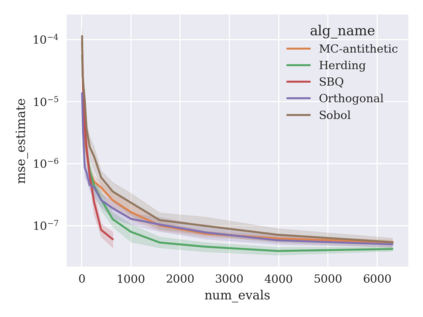
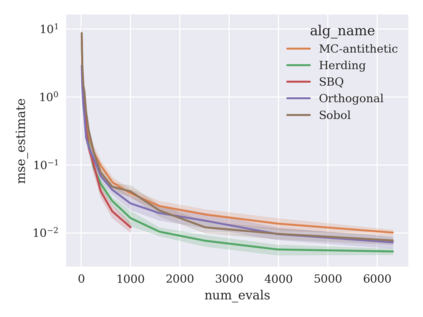
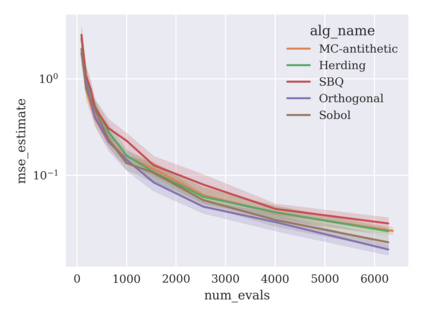
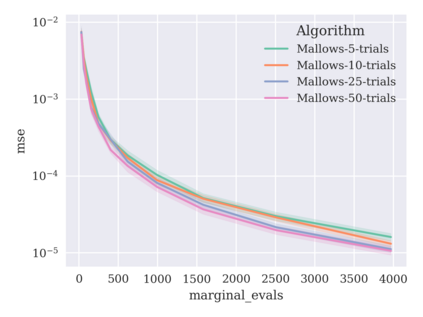
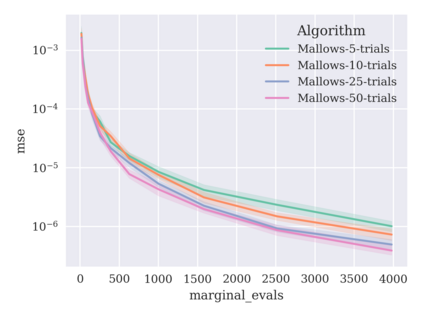
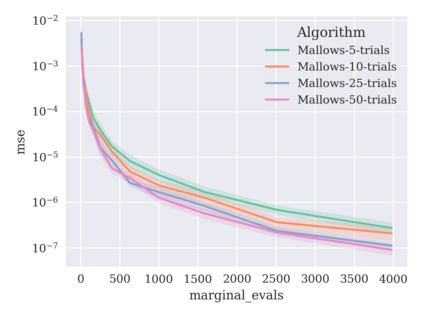
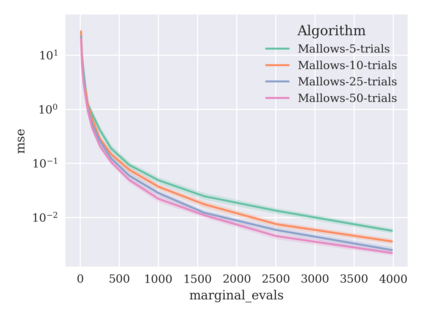
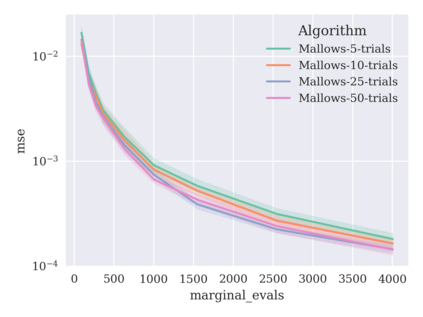
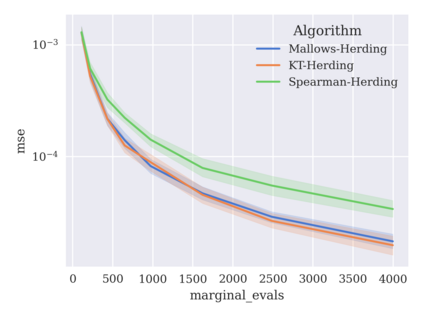
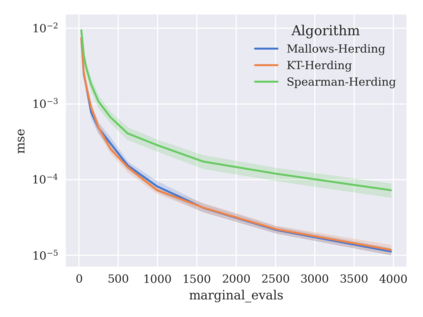
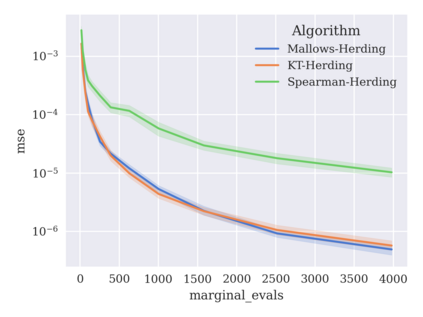
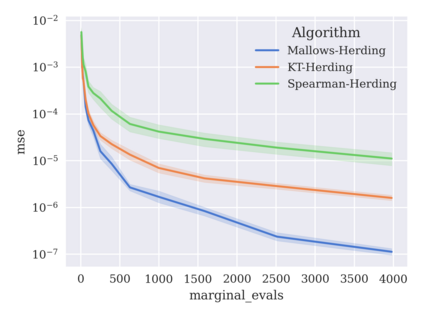
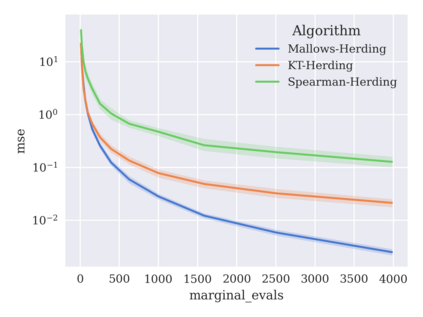
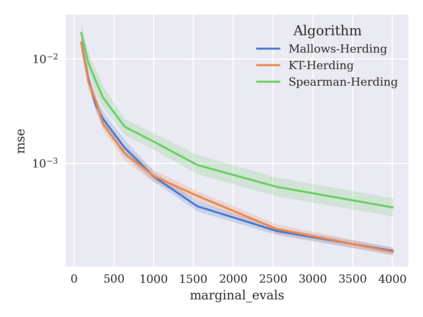
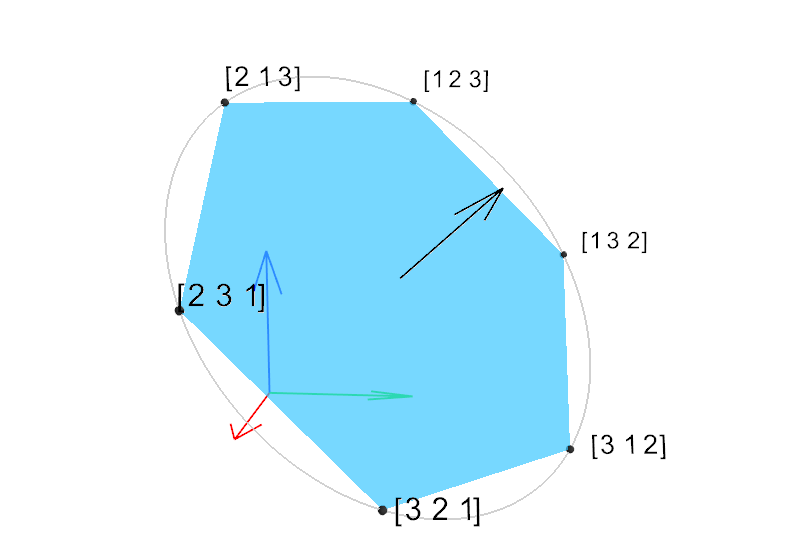
Game-theoretic attribution techniques based on Shapley values are used to interpret black-box machine learning models, but their exact calculation is generally NP-hard, requiring approximation methods for non-trivial models. As the computation of Shapley values can be expressed as a summation over a set of permutations, a common approach is to sample a subset of these permutations for approximation. Unfortunately, standard Monte Carlo sampling methods can exhibit slow convergence, and more sophisticated quasi-Monte Carlo methods have not yet been applied to the space of permutations. To address this, we investigate new approaches based on two classes of approximation methods and compare them empirically. First, we demonstrate quadrature techniques in a RKHS containing functions of permutations, using the Mallows kernel in combination with kernel herding and sequential Bayesian quadrature. The RKHS perspective also leads to quasi-Monte Carlo type error bounds, with a tractable discrepancy measure defined on permutations. Second, we exploit connections between the hypersphere $\mathbb{S}^{d-2}$ and permutations to create practical algorithms for generating permutation samples with good properties. Experiments show the above techniques provide significant improvements for Shapley value estimates over existing methods, converging to a smaller RMSE in the same number of model evaluations.
翻译:基于遮蔽值的游戏理论归因技术被用于解释黑盒机器学习模型,但精确的计算方法一般是NP-硬的,要求非三角模型采用近似方法。由于可以将遮蔽值的计算作为一组变相的总和来表示,一种共同的方法是抽样这些变异的子集。不幸的是,标准的蒙特卡洛采样方法可能显示缓慢的趋同,而更先进的准蒙太罗方法尚未应用于变异空间。为了解决这个问题,我们根据两种近似方法来调查新的方法,并进行实验性比较。首先,我们在包含变异函数的RKHS中展示二次方位技术,使用Mallows内核结合内核和Bayesan的二次方位。RKHS的视角还会导致半蒙特·卡洛型错误的界限,同时根据变异度确定一个模型。第二,我们利用超视距 $\mathb{S ⁇ 2} $ 和 permutiming 方法进行二次对比。我们展示了二次的二次变形技术,以便用实际的模型对数值作出重大分析。