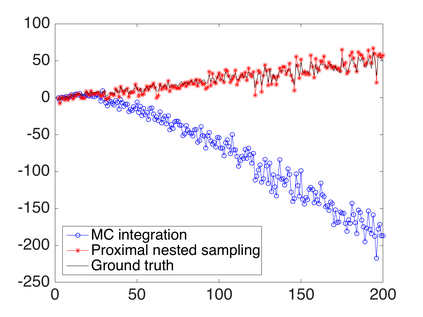
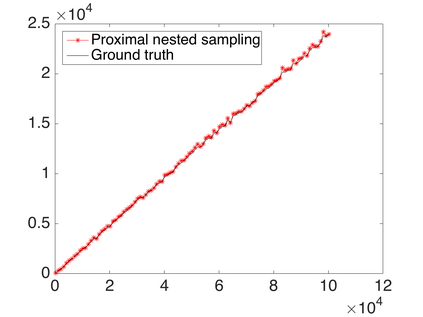
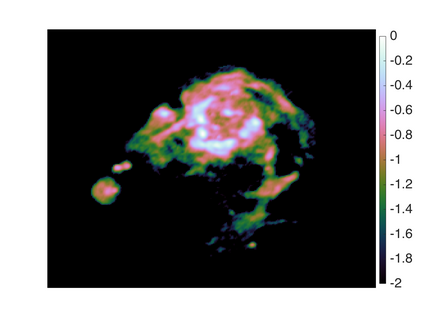
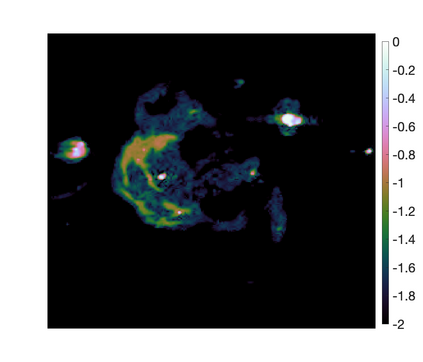
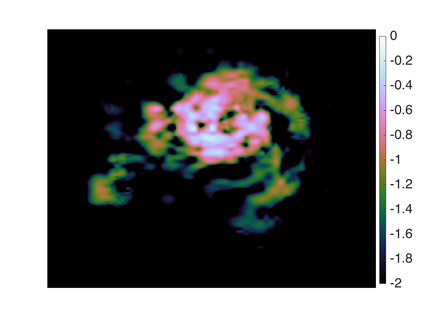
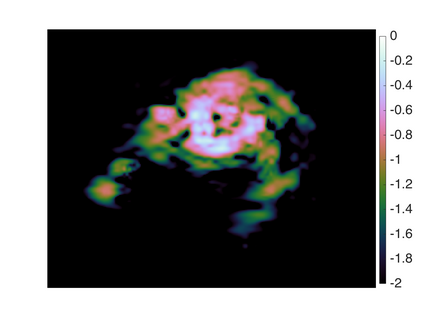
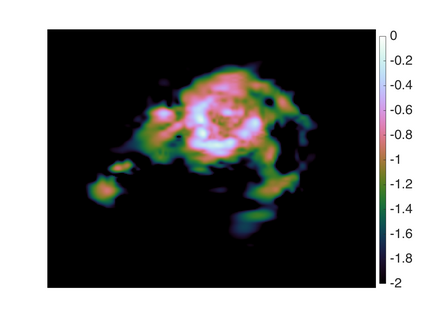
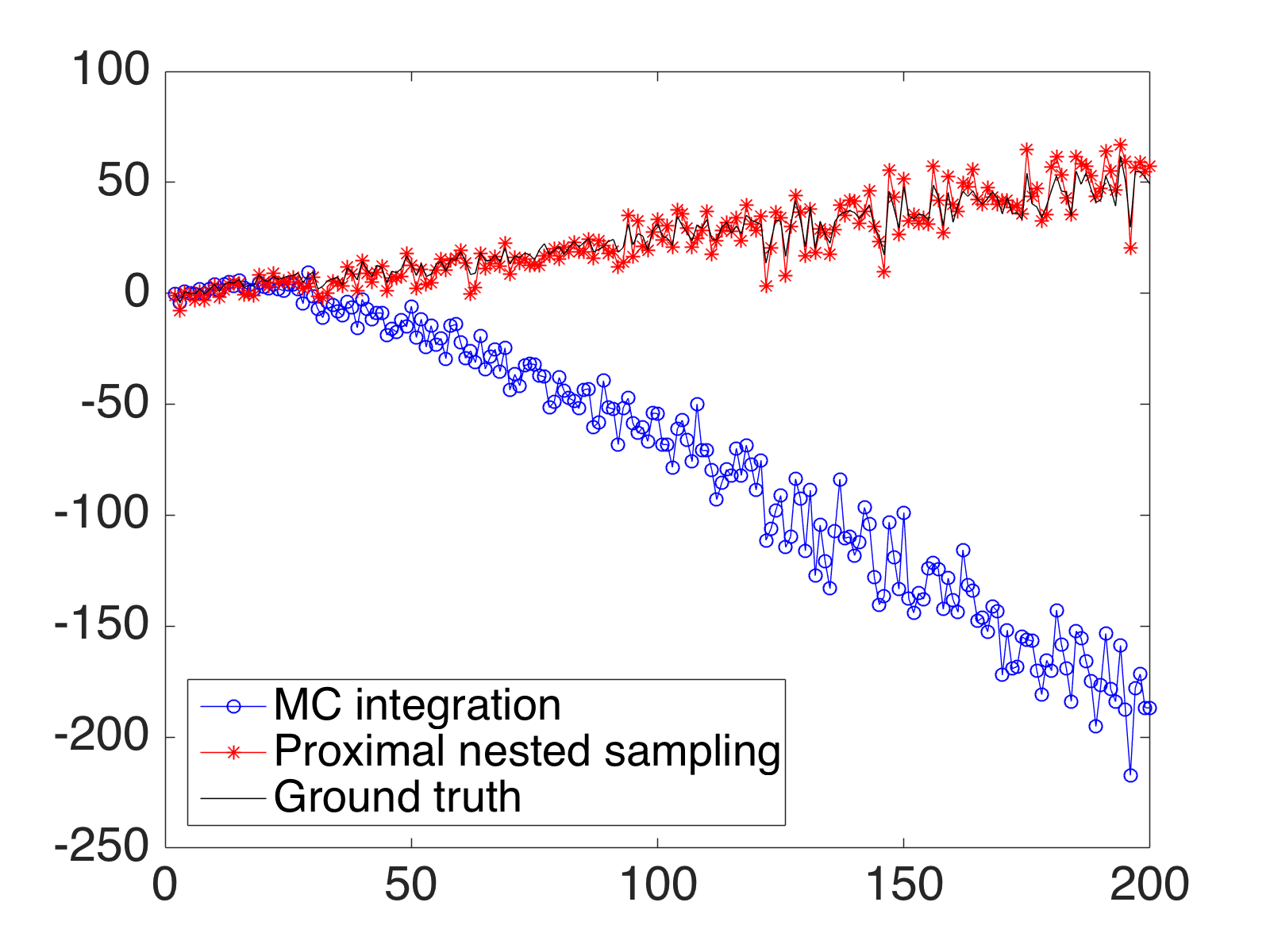
Bayesian model selection provides a powerful framework for objectively comparing models directly from observed data, without reference to ground truth data. However, Bayesian model selection requires the computation of the marginal likelihood (model evidence), which is computationally challenging, prohibiting its use in many high-dimensional Bayesian inverse problems. With Bayesian imaging applications in mind, in this work we present the proximal nested sampling methodology to objectively compare alternative Bayesian imaging models for applications that use images to inform decisions under uncertainty. The methodology is based on nested sampling, a Monte Carlo approach specialised for model comparison, and exploits proximal Markov chain Monte Carlo techniques to scale efficiently to large problems and to tackle models that are log-concave and not necessarily smooth (e.g., involving l_1 or total-variation priors). The proposed approach can be applied computationally to problems of dimension O(10^6) and beyond, making it suitable for high-dimensional inverse imaging problems. It is validated on large Gaussian models, for which the likelihood is available analytically, and subsequently illustrated on a range of imaging problems where it is used to analyse different choices of dictionary and measurement model.
翻译:Bayesian 模型选择提供了一个强有力的框架,可以直接从观测到的数据中客观比较模型,而不必参考地面真相数据。然而,Bayesian 模型选择要求计算边际可能性(模型证据),这种可能性在计算上具有挑战性,禁止将其用于许多高维Bayesian反向问题。考虑到Bayesian 成像应用,在这项工作中,我们提出了近乎于鸟巢的取样方法,以客观地比较替代Bayesian成像模型,用于在不确定情况下使用图像作为决策依据的应用。该方法以嵌套抽样为基础,一种专门用于模型比较的Monte Carlo 方法,并且利用Monte Carlo 链的准ximal Markov 技术,以便有效地将问题推广到大范围,并解决日志组合和不一定平稳的模型(例如,涉及 l_1 或 全部变换之前的模型) 。拟议方法可以用于对维度 O (10 ⁇ 6) 及以后的问题进行计算,使之适合高度反向成像学问题。该方法在大型的模型上得到验证,并随后对各种模型加以说明,用于分析。