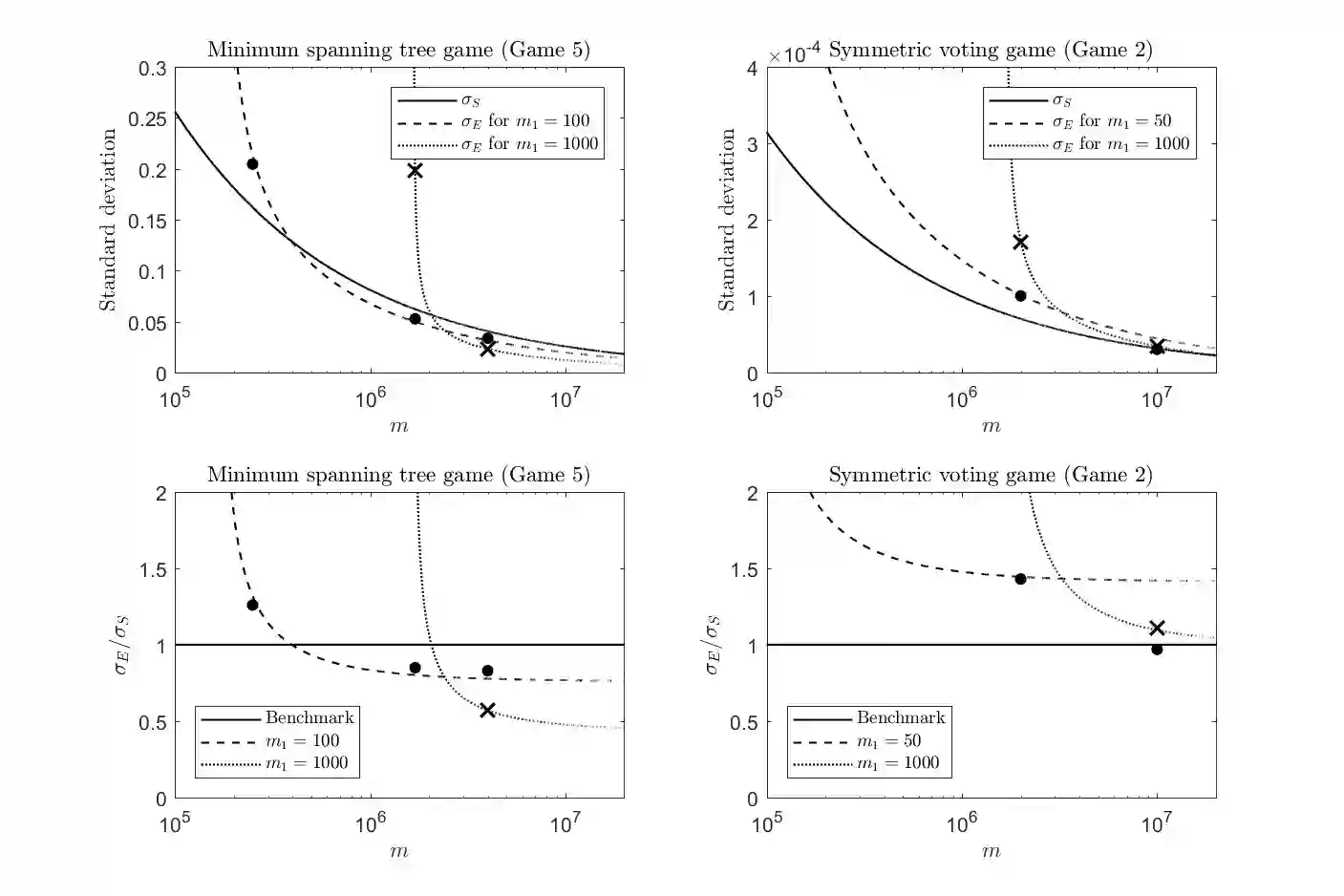
The idea of approximating the Shapley value of an n-person game by Monte Carlo simulation was first suggested by Mann and Shapley (1960) and they also introduced four different heuristical methods to reduce the estimation error. Since 1960, several statistical methods have been developed to reduce the standard deviation of the estimate. In this paper, we develop an algorithm that uses a pair of negatively correlated samples to reduce the variance of the estimate. Although the observations generated are not independent, the sample is ergodic (obeys the strong law of large numbers), hence the name "ergodic sampling". Unlike Shapley and Mann, we do not use heuristics, the algorithm uses a small sample to learn the best ergodic transformation for a given game. We illustrate the algorithm on eight games with different characteristics to test the performance and understand how the proposed algorithm works. The experiments show that this method has at least as low variance as an independent sample, and in five test games, it significantly improves the quality of the estimation, up to 75 percent.
翻译:蒙得卡洛模拟(1960年)的近似光滑值概念由蒙特卡洛模拟(Main and Shapley)(Main and Shapley)(1960年)首次提出,它们也采用了四种不同的理论方法来减少估计误差。自1960年以来,已经开发了几种统计方法来减少估计标准偏差。在本文中,我们开发了一种算法,使用一对负相关样本来减少估计值的差异。虽然产生的观测不是独立的,但样本是自成一体的(超越大量数字的强势定律),因此名称是“ergodic抽样 ” 。 与Shapley and Mann不同,我们没有使用超自然学方法,算法方法使用一个小样本来学习某一游戏的最佳电磁变形。 我们用八个具有不同特性的游戏的算法来测试性能并了解提议的算法如何运作。实验显示,这种方法至少与独立的样本有低差异,在五个测试游戏中,它极大地提高了估计质量,达75%。