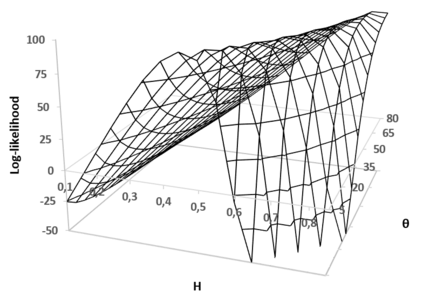
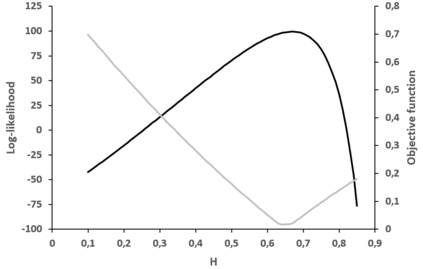
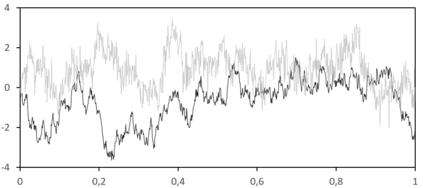
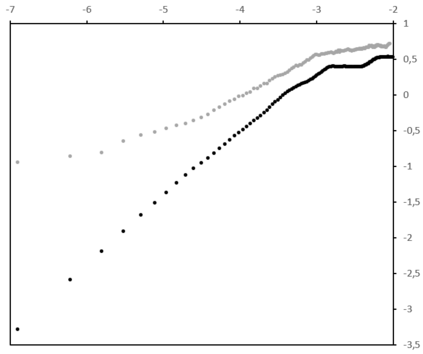
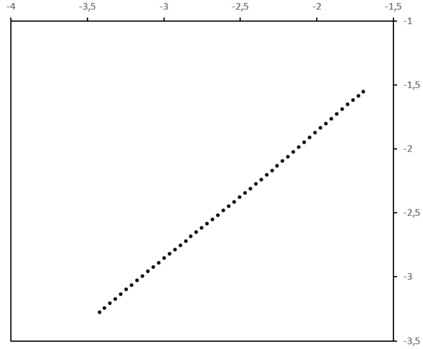
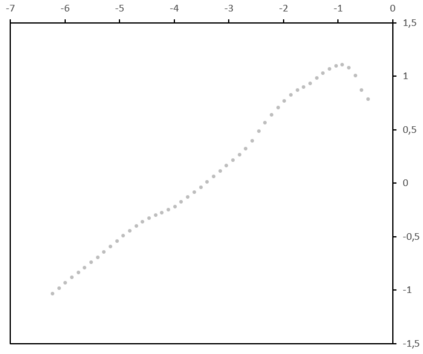
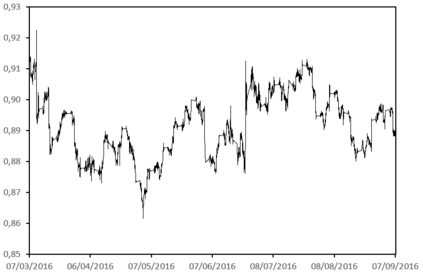
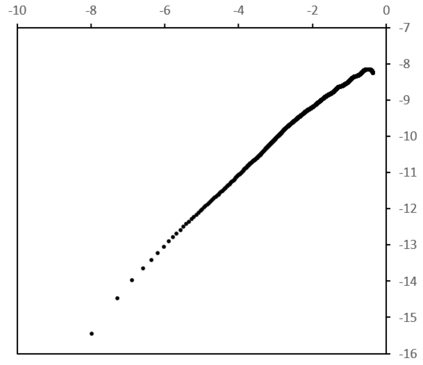
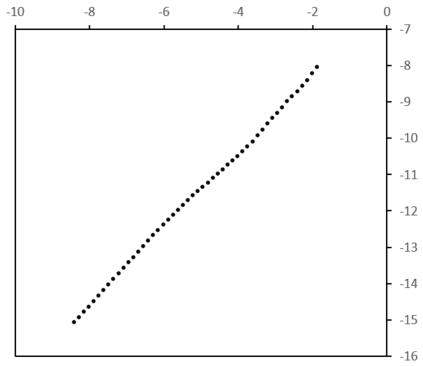
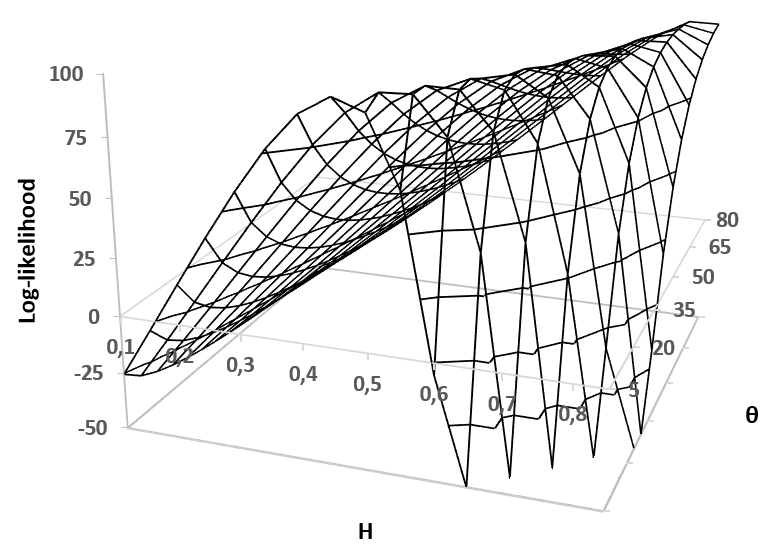
The absolute-moment method is widespread for estimating the Hurst exponent of a fractional Brownian motion $X$. But this method is biased when applied to a stationary version of $X$, in particular an inverse Lamperti transform of $X$, with a linear time contraction of parameter $\theta$. We present an adaptation of the absolute-moment method to this framework and we compare it to the maximum likelihood method, with simulations and an application to a financial time series. While it appears that the maximum-likelihood method is more accurate than the adapted absolute-moment estimation, this last method is not uninteresting for two reasons: it makes it possible to confirm visually that the model is well specified and it is computationally more performing.
翻译:绝对时速法在估算一个分数的布朗运动的赫斯特指数X$方面十分普遍。但是,这种方法在适用于固定版本的X美元时是有偏向的,特别是兰佩蒂的逆变换为X美元,其线性时间缩缩缩为$@theta$。我们对这一框架提出了绝对时速法的调整,并将它与最大可能性法、模拟和对财务时间序列的应用进行比较。虽然似乎最大相似性法比经调整的绝对时速估计更准确,但最后一种方法并非不感兴趣,原因有二:它使得有可能从视觉上证实模型非常具体,计算效果更佳。