最大均方差正则化贝叶斯神经网络，Bayesian Neural Networks With Maximum Mean Discrepancy Regularization

题目： Bayesian Neural Networks With Maximum Mean Discrepancy Regularization

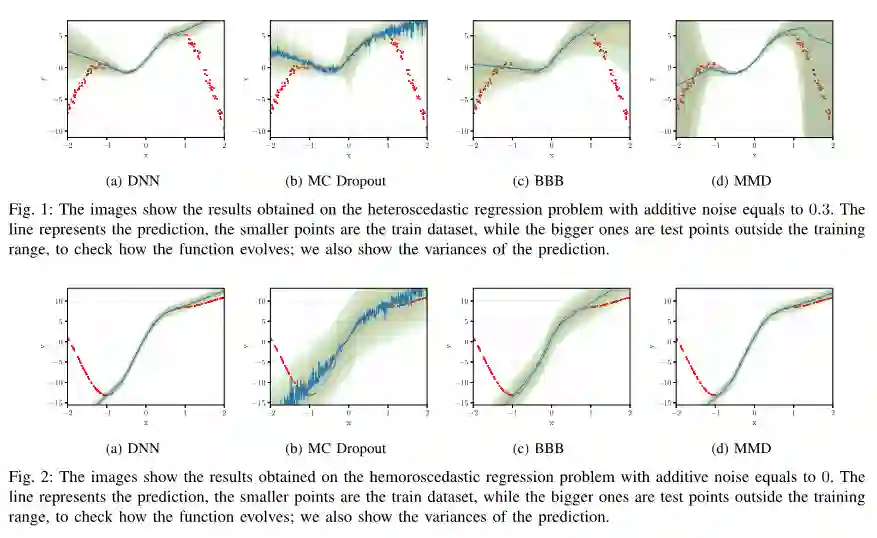
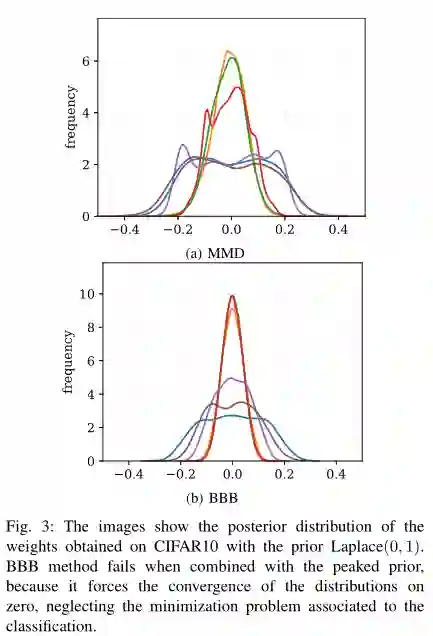
摘要： 贝叶斯神经网络(BNNs)训练来优化整个分布的权重，而不是一个单一的集合，在可解释性、多任务学习和校准等方面具有显著的优势。由于所得到的优化问题的难解性，大多数BNNs要么通过蒙特卡罗方法采样，要么通过在变分近似上最小化一个合适的样本下界(ELBO)来训练。在这篇论文中，我们提出了后者的一个变体，其中我们用最大平均偏差(MMD)估计器代替了ELBO项中的Kullback-Leibler散度，这是受到了最近的变分推理工作的启发。在根据MMD术语的性质提出我们的建议之后，我们接着展示了公式相对于最先进的公式的一些经验优势。特别地，我们的BNNs在多个基准上实现了更高的准确性，包括多个图像分类任务。此外，它们对权重上的先验选择更有鲁棒性，而且它们的校准效果更好。作为第二项贡献，我们提供了一个新的公式来估计给定预测的不确定性，表明与更经典的标准(如微分熵)相比，它在对抗攻击和输入噪声的情况下表现得更稳定。