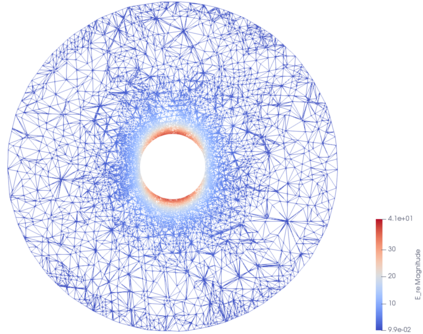
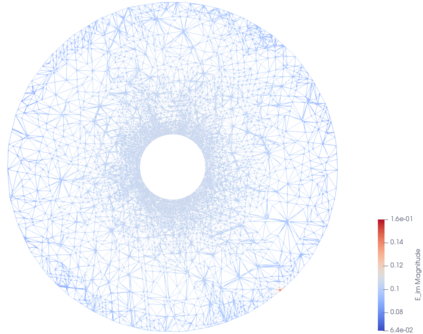
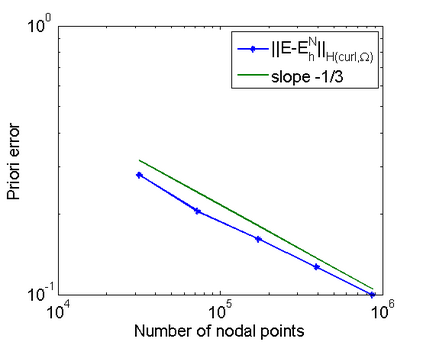
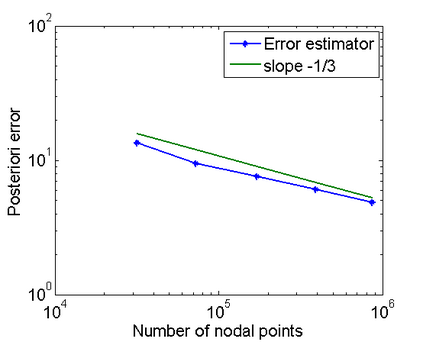
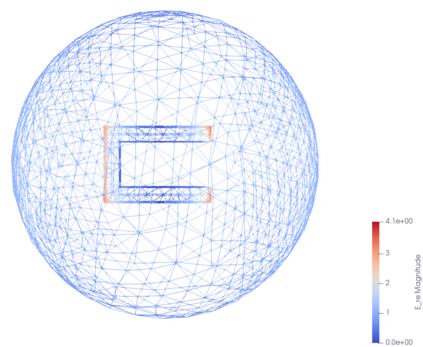
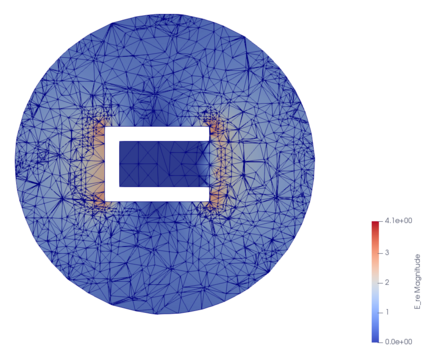
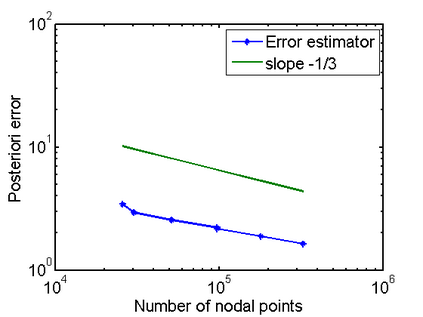
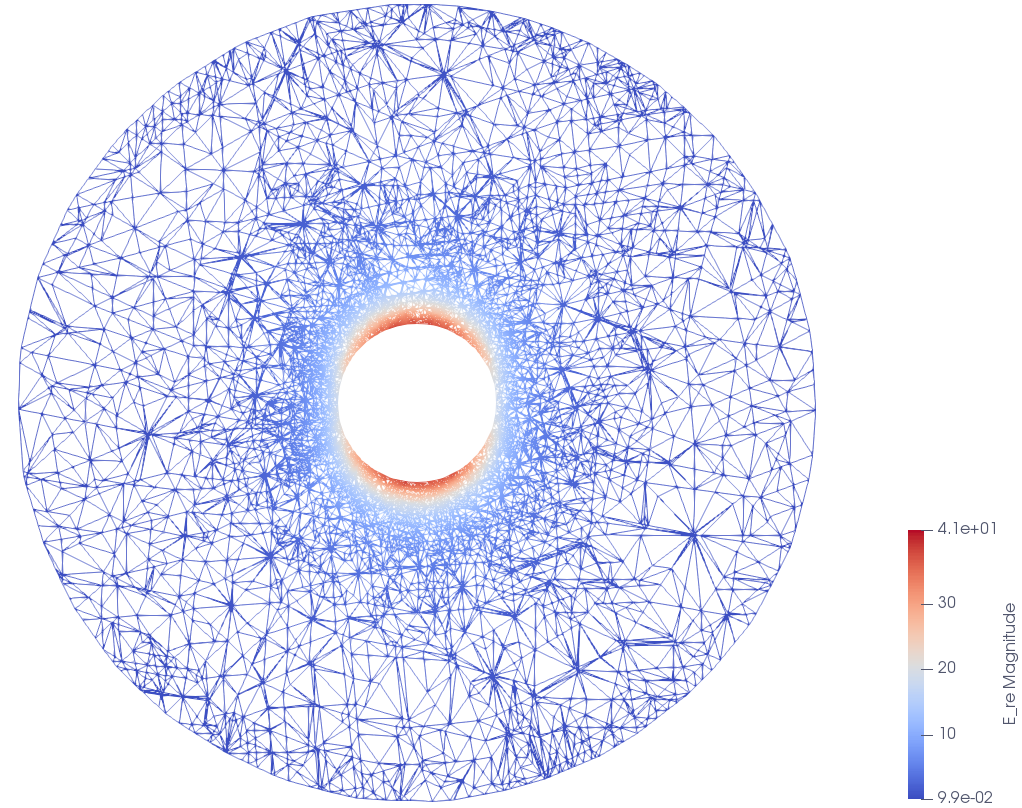
This paper is concerned with a numerical solution to the scattering of a time-harmonic electromagnetic wave by a bounded and impenetrable obstacle in three dimensions. The electromagnetic wave propagation is modeled by a boundary value problem of Maxwell's equations in the exterior domain of the obstacle. Based on the Dirichlet-to-Neumann (DtN) operator, which is defined by an infinite series, an exact transparent boundary condition is introduced and the scattering problem is reduced equivalently into a bounded domain. An a posteriori error estimate based adaptive finite element DtN method is developed to solve the discrete variational problem, where the DtN operator is truncated into a sum of finitely many terms. The a posteriori error estimate takes into account both the finite element approximation error and the truncation error of the DtN operator. The latter is shown to decay exponentially with respect to the truncation parameter. Numerical experiments are presented to illustrate the effectiveness of the proposed method.
翻译:本文涉及一个数字解决方案,用三个维度的封闭和不可阻隔的障碍将时间-和谐电磁波散布在三个维度上。 电磁波的传播以障碍体外域的马克斯韦尔方程式的边界值问题为模型。 基于由无限序列定义的Drichlet- to-Neumann(DtN)操作员, 引入了精确透明的边界条件, 将散射问题同等地缩小到一个封闭域。 基于适应性有限元素 DtN 的事后误差估计方法, 以解决离散变化问题, DtN 操作员被挤压成数量有限的多个术语的总和。 事后错误估计既考虑到有限元素近似误差,又考虑到DtN 操作员的脱轨误差。 后一种误差在轨参数上显示出指数化的指数衰减。 以 Numical 实验展示了拟议方法的有效性 。