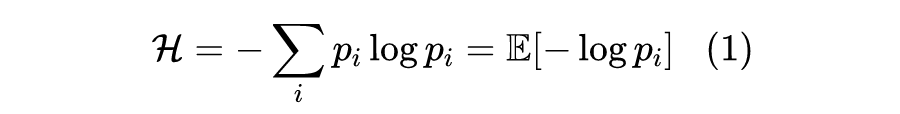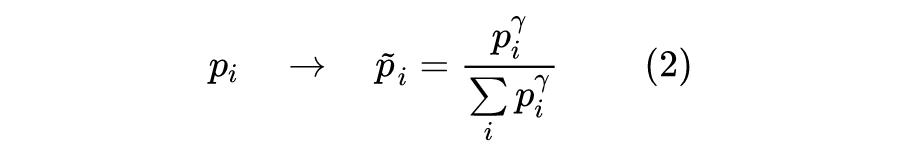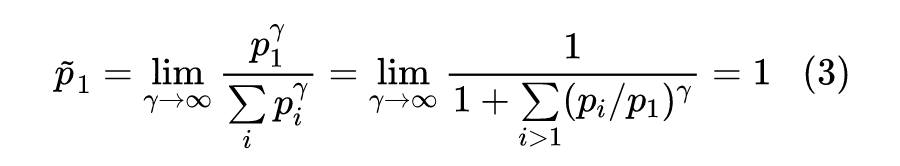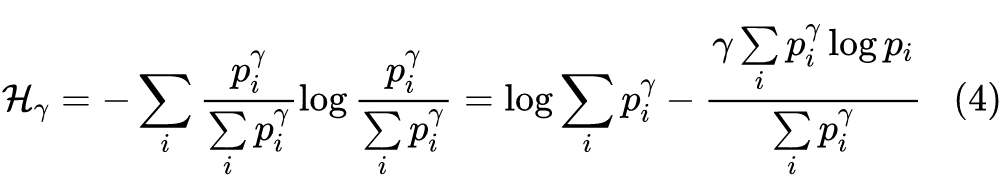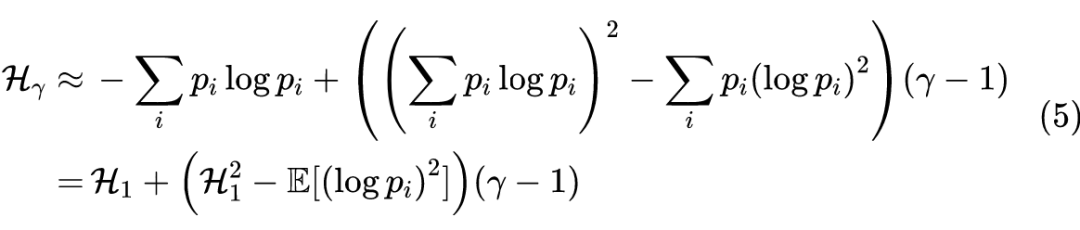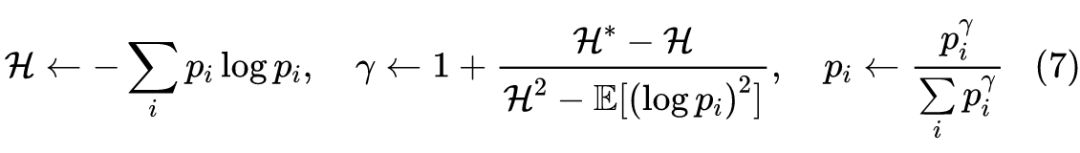概率分布的熵归一化（Entropy Normalization）

2022 年 1 月 3 日 PaperWeekly

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 追一科技

研究方向 | NLP、神经网络

在上一篇文章《从熵不变性看 Attention 的 Scale 操作》中，我们从熵不变性的角度推导了一个新的 Attention Scale，并且实验显示具有熵不变性的新 Scale 确实能使得 Attention 的外推性能更好。这时候笔者就有一个很自然的疑问：

有没有类似 L2 Normalization 之类的操作，可以直接对概率分布进行变换，使得保持原始分布主要特性的同时，让它的熵为指定值？

笔者带着疑问搜索了一番，发现没有类似的研究，于是自己尝试推导了一下，算是得到了一个基本满意的结果，暂称为“熵归一化（Entropy Normalization）”，记录在此，供有需要的读者参考。

幂次变换

首先，假设元分布，它的熵定义为：

由于，所以，因此，当某个为 1、其余为 0 时（one hot），取得最小值 0；此外，也可以证明当所有等于时，取得最大值，所以的取值范围是。

所以，我们首先要找一种分布的变换，它能够保持分布的主要信息，并且有能力将分布的熵从 0 到进行变换。这里选择的是幂次变换：

选择幂次变换的原因之一，是它保持了分布的单调性，即如果，那么也有，个人认为这是分布需要保持的重要性质之一。此外，当各个都非零并且两两不相等时，幂次变化确实有能力将熵从进行变化。不失一般性，我们假设，显然当时，，此时熵为最大值，当时，有：

也就是此时为 one hot 分布，对应的熵为最小值 0。其实还可以进一步求导证明熵关于是单调递减的，因此当从 0 到递增时，熵从到 0 递减变化。

迭代求解

确定幂次变换确实是一种可用的变换后，我们就需要进入求解流程了，即对于任意给定的，我们需要找到正确的，使得对应的熵为指定值。

首先我们写出：

最右端结果的复杂性让我们相信应该不存在解析解，所以只能寻求迭代求解算法了。

我们求它在处的展开（主要利用

：

那么：

根据该结果，我们从出发，反复利用上式进行迭代，就可以求出最终的分布：

这其实就是求解非线性方程的牛顿法了。在实验时发现，迭代 3～4 次，就可以取得不错的收敛效果，如果实际使用时只是为了大致地控制一下熵的范围，那么迭代 1～2 次即可。

Numpy 的参考代码：

 1p = np.random.random(100)
 2p /= p.sum()  # 模拟分布
 3gamma = 1
 4H_f = np.log(30)  # 希望达到的熵
 5
 6for i in range(10):
 7    H = -(p * np.log(p)).sum()
 8    gamma = 1 + (H_f - H) / (H**2 - (p * np.log(p)**2).sum())
 9    p = p**gamma
10    p /= p.sum()

应用设想

本文主要是觉得“熵归一化”这个概念比较有意思，所以尝试进行了推导。但具体有什么比较好的应用例子，笔者也还没想清楚。

熵越小，意味着概率越集中在几个位置上，换句话说就是其他位置的概率越接近于零，因此某种程度上来说，熵是概率分布的稀疏程度的一种度量，如果我们希望得到比较稀疏的预测结果，那么就可以通过熵归一化进行控制。另一方面，分布越稀疏，也意味着模型越有可能梯度消失，因此反过来也可以通过熵归一化来控制熵不要那么小，从而缓解梯度消失问题。

说到稀疏性，就不免想起 Sparsemax [1] 以及笔者自己构思的 Sparse Softmax 等工作，其中 Sparsemax 是将熵视为惩罚项来得到的稀疏性，而 Sparse Softmax 则是通过直接截断而引入的稀疏性，两者皆在某些场景下有更好的解释性或者更好的效果，那么直接通过熵归一化带来的稀疏性有没有效果呢？这可能也是一个值得探究的问题。