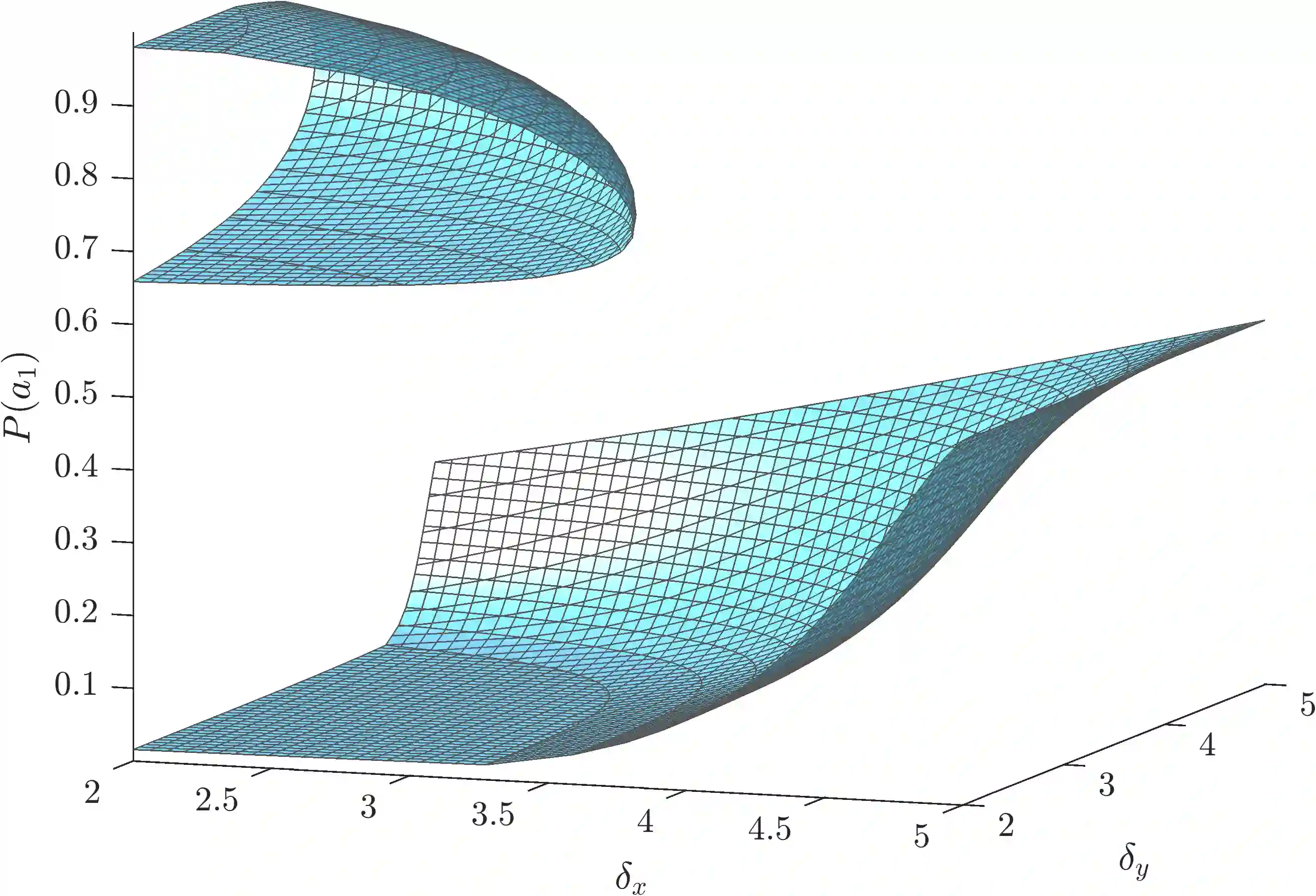
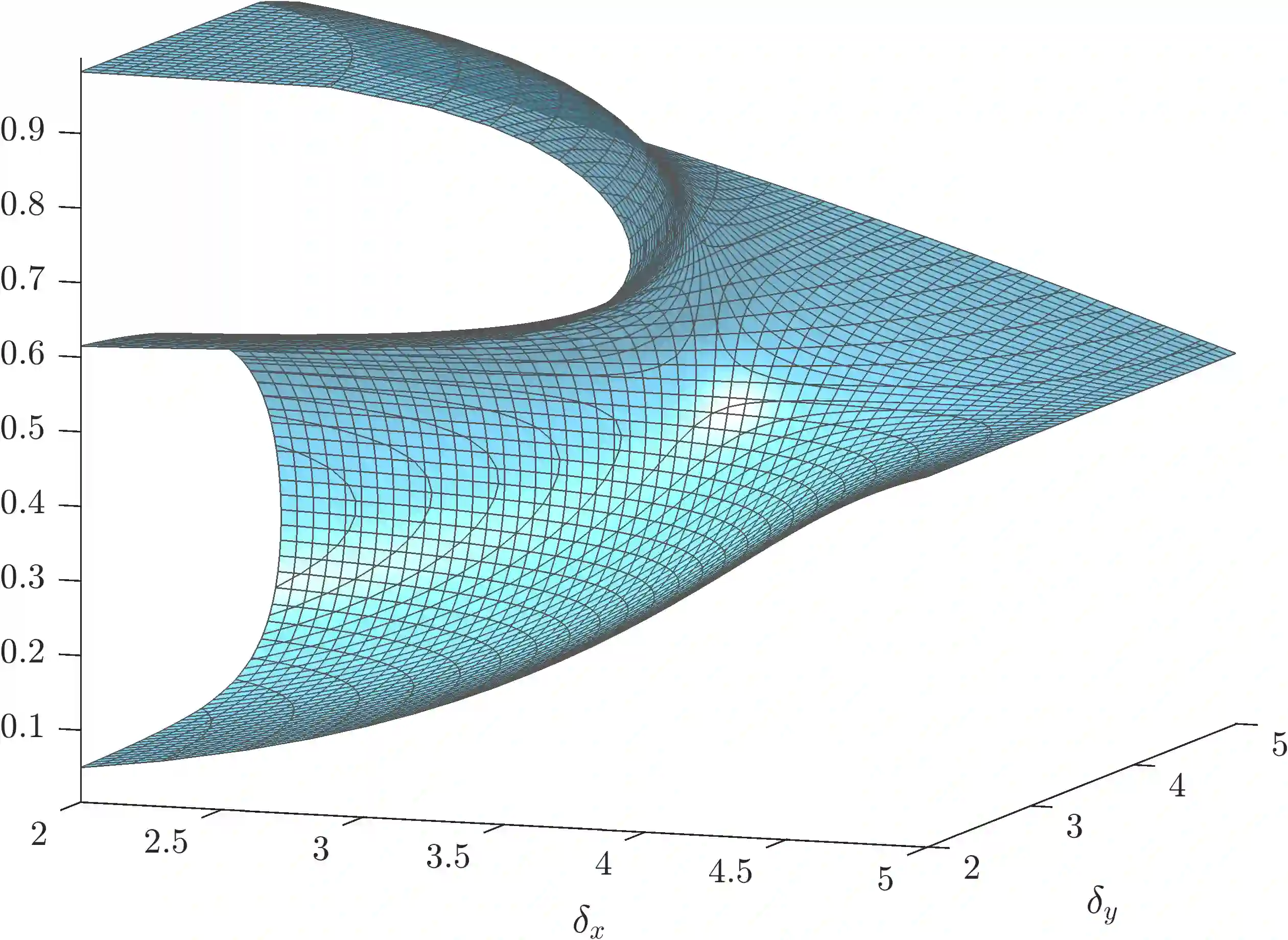
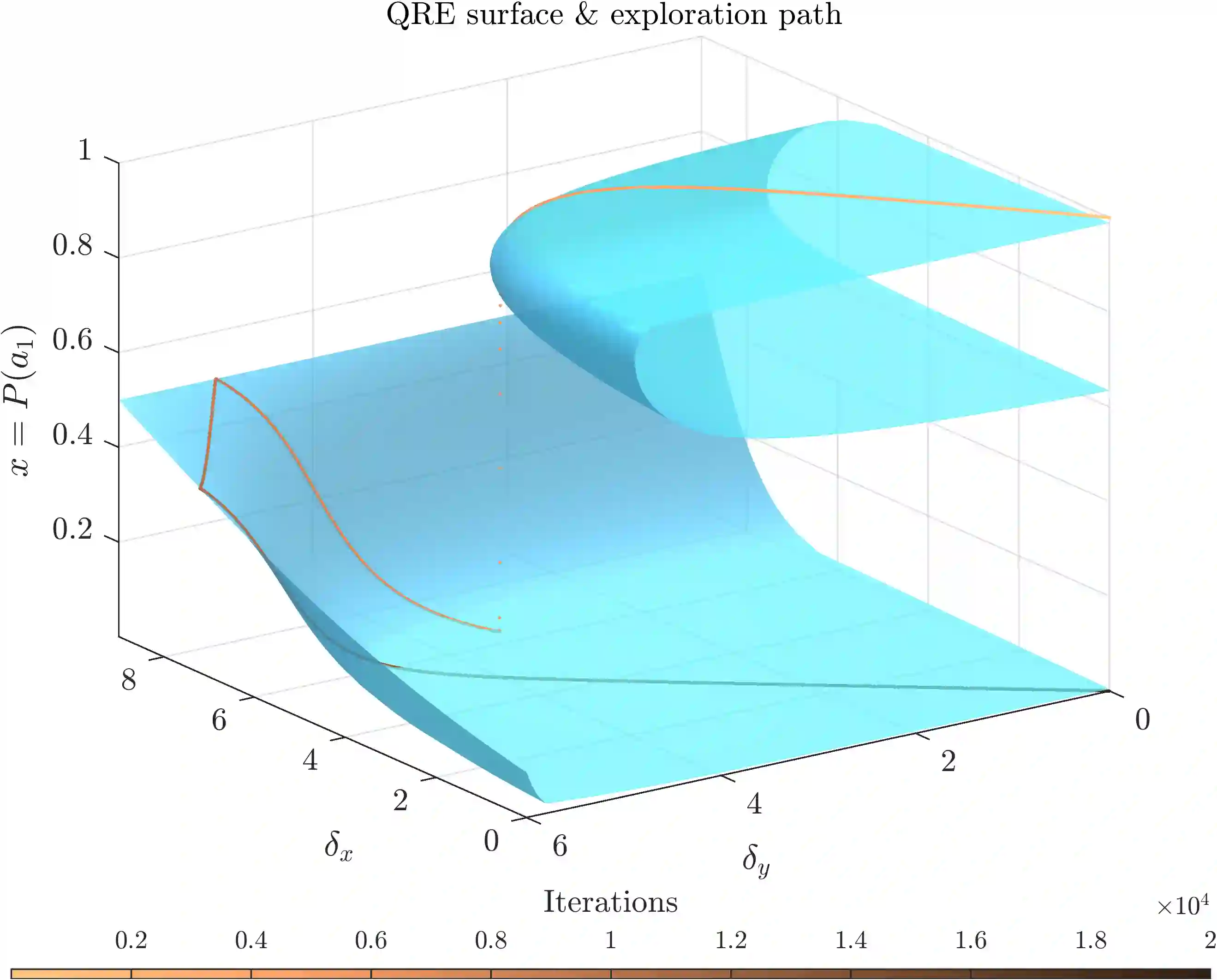
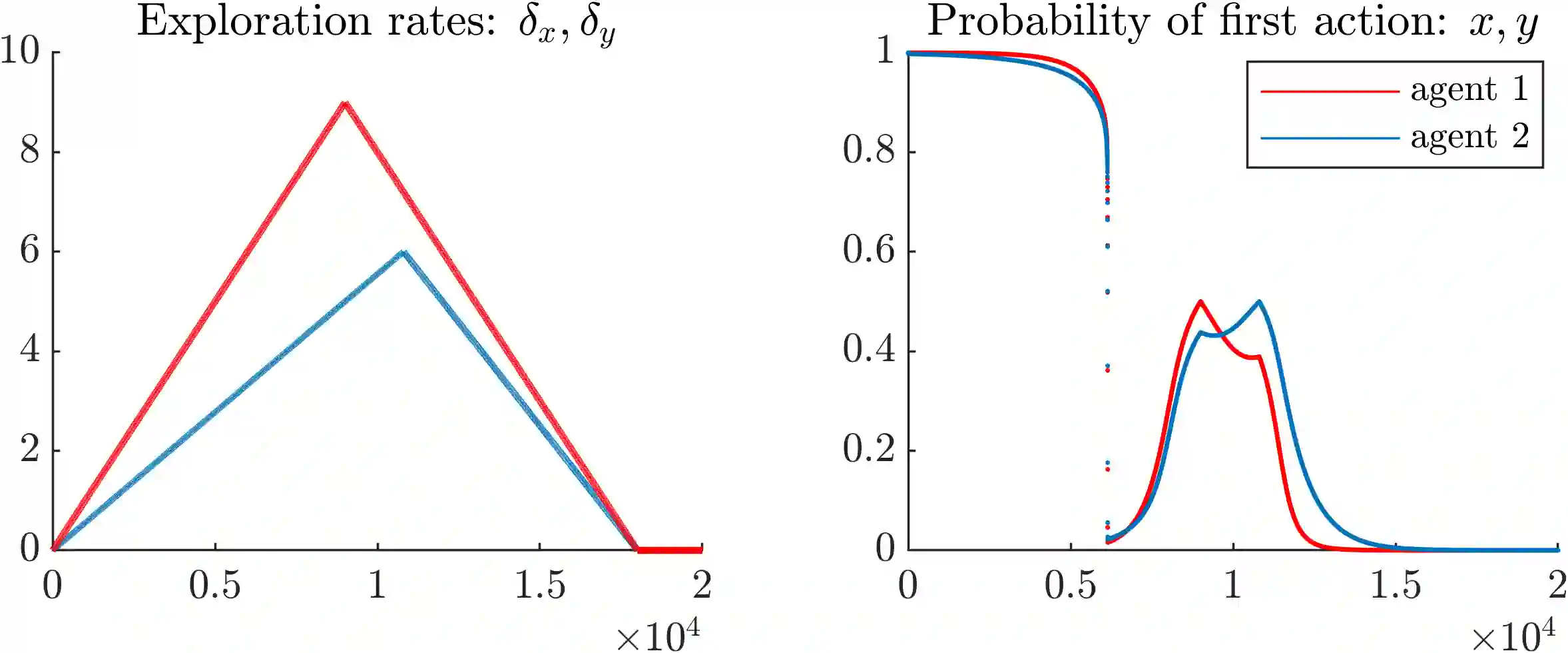
Exploration-exploitation is a powerful and practical tool in multi-agent learning (MAL), however, its effects are far from understood. To make progress in this direction, we study a smooth analogue of Q-learning. We start by showing that our learning model has strong theoretical justification as an optimal model for studying exploration-exploitation. Specifically, we prove that smooth Q-learning has bounded regret in arbitrary games for a cost model that explicitly captures the balance between game and exploration costs and that it always converges to the set of quantal-response equilibria (QRE), the standard solution concept for games under bounded rationality, in weighted potential games with heterogeneous learning agents. In our main task, we then turn to measure the effect of exploration in collective system performance. We characterize the geometry of the QRE surface in low-dimensional MAL systems and link our findings with catastrophe (bifurcation) theory. In particular, as the exploration hyperparameter evolves over-time, the system undergoes phase transitions where the number and stability of equilibria can change radically given an infinitesimal change to the exploration parameter. Based on this, we provide a formal theoretical treatment of how tuning the exploration parameter can provably lead to equilibrium selection with both positive as well as negative (and potentially unbounded) effects to system performance.
翻译:探索探索开发是多试剂学习(MAL)中一个强大而实用的工具,然而,它的效果远未被理解。为了朝这个方向取得进展,我们研究一个平稳的Q-学习模拟。我们首先显示我们的学习模式有很强的理论理由,是研究探索-开发的最佳模式。具体地说,我们证明,顺利的Q-学习在任意游戏中,对明确体现游戏和勘探成本平衡的成本模型(MAL)感到遗憾,而且它总是会与一套四等反应平衡(QRE)(QRE)(QRE)(QRE)(QRE)(QRE)(QRE))(QRE))(QRE)(QRE))(QRE)(QRE)(QRE)(QRE)(Q-L)(Q-L)(Q-L)(M)(M) (M) (M) (M) (M) (M) (M) (O) (O) (O) (O(Q) (I) (O) (I) (I) (I) (O(S) (O) (O) (O) (S) (O) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (O) (O) (O) (O) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (S) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I) (I)