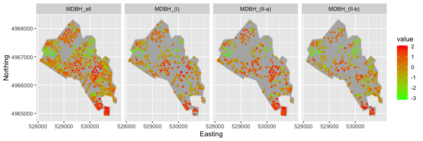
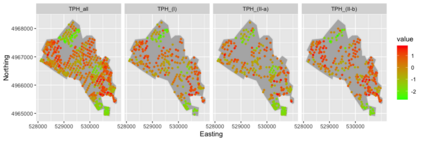
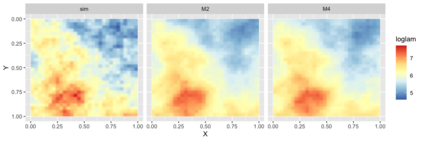
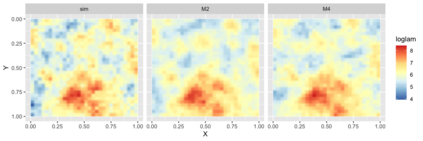
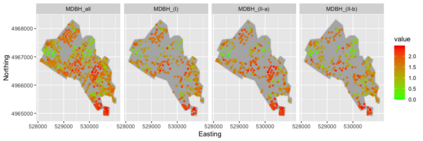
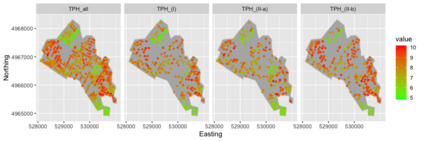
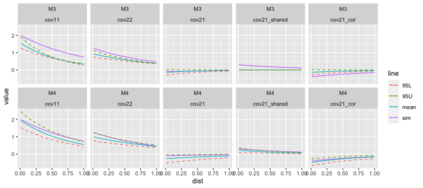
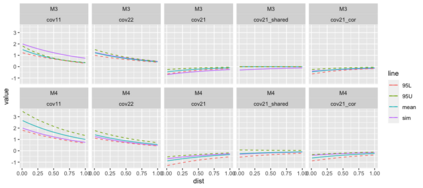
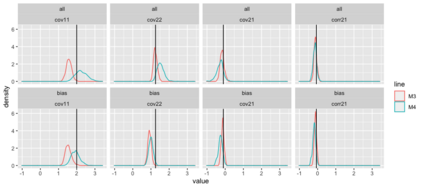
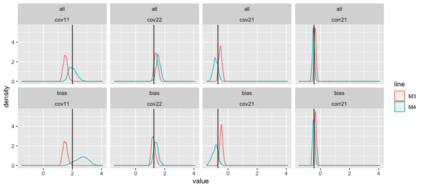
Preferential Sampling for Bivariate Spatial Data

Preferential sampling provides a formal modeling specification to capture the effect of bias in a set of sampling locations on inference when a geostatistical model is used to explain observed responses at the sampled locations. In particular, it enables modification of spatial prediction adjusted for the bias. Its original presentation in the literature addressed assessment of the presence of such sampling bias while follow on work focused on regression specification to improve spatial interpolation under such bias. All of the work in the literature to date considers the case of a univariate response variable at each location, either continuous or modeled through a latent continuous variable. The contribution here is to extend the notion of preferential sampling to the case of bivariate response at each location. This exposes sampling scenarios where both responses are observed at a given location as well as scenarios where, for some locations, only one of the responses is recorded. That is, there may be different sampling bias for one response than for the other. It leads to assessing the impact of such bias on co-kriging. It also exposes the possibility that preferential sampling can bias inference regarding dependence between responses at a location. We develop the idea of bivariate preferential sampling through various model specifications and illustrate the effect of these specifications on prediction and dependence behavior. We do this both through simulation examples as well as with a forestry dataset that provides mean diameter at breast height (MDBH) and trees per hectare (TPH) as the point-referenced bivariate responses.