Neural Stochastic Partial Differential Equations: Resolution-Invariant Learning of Continuous Spatiotemporal Dynamics

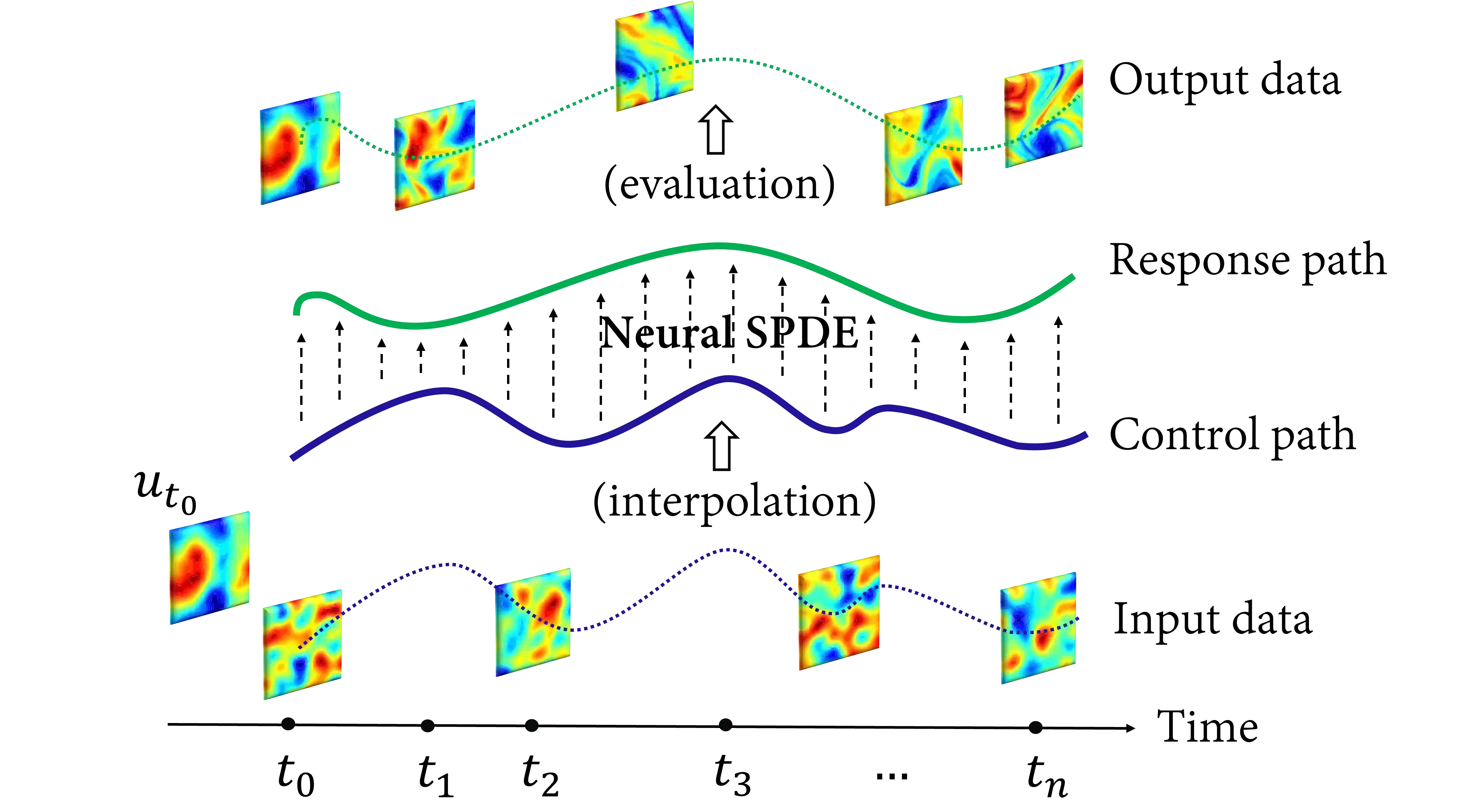
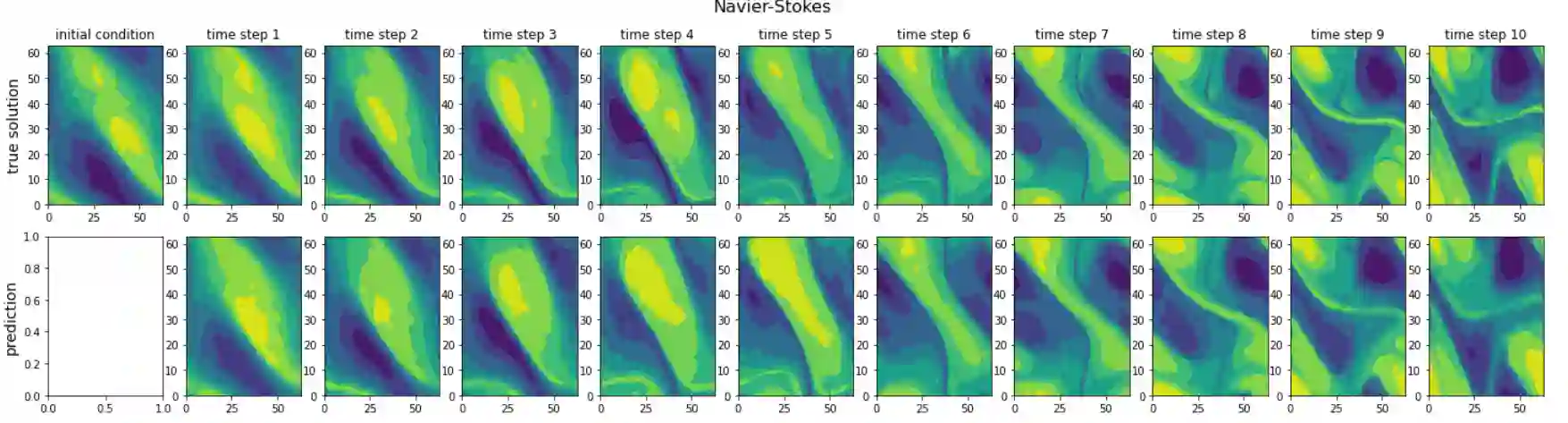
Stochastic partial differential equations (SPDEs) are the mathematical tool of choice for modelling spatiotemporal PDE-dynamics under the influence of randomness. Based on the notion of mild solution of an SPDE, we introduce a novel neural architecture to learn solution operators of PDEs with (possibly stochastic) forcing from partially observed data. The proposed Neural SPDE model provides an extension to two popular classes of physics-inspired architectures. On the one hand, it extends Neural CDEs and variants -- continuous-time analogues of RNNs -- in that it is capable of processing incoming sequential information arriving irregularly in time and observed at arbitrary spatial resolutions. On the other hand, it extends Neural Operators -- generalizations of neural networks to model mappings between spaces of functions -- in that it can parameterize solution operators of SPDEs depending simultaneously on the initial condition and a realization of the driving noise. By performing operations in the spectral domain, we show how a Neural SPDE can be evaluated in two ways, either by calling an ODE solver (emulating a spectral Galerkin scheme), or by solving a fixed point problem. Experiments on various semilinear SPDEs, including the stochastic Navier-Stokes equations, demonstrate how the Neural SPDE model is capable of learning complex spatiotemporal dynamics in a resolution-invariant way, with better accuracy and lighter training data requirements compared to alternative models, and up to 3 orders of magnitude faster than traditional solvers.