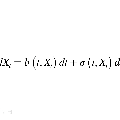泛函不等式与随机微分方程上的大偏差问题

项目名称： 泛函不等式与随机微分方程上的大偏差问题

项目编号： No.11371283

项目类型： 面上项目

立项/批准年度： 2013

项目学科： 数理科学和化学

项目作者： 张正良

作者单位： 武汉大学

项目金额： 55万元

中文摘要： 该项目主要研究概率论中的几个泛函不等式，这其中包括亚椭圆算子的泛函不等式，随机微分方程，如反映扩散方程，滞后系统，Burgers方程，Navier-Stokes方程等轨道空间上的泛函不等式以及一些含参变量的具有实际意义的测度和分布,如调和测度，Moebius测度，Boltzmann测度，柯西分布等的泛函不等式，并由此进一步印证对数Sobolev不等式与传输不等式的严格强弱关系。此外，我们还将研究带随机小扰动的随机微分方程上的大偏差，中偏差，中心极限定理。

中文关键词： 泛函不等式；随机微分方程；大偏差；；

英文摘要： This project will be devoted to the research on functional inequalities in probability theory: including for hypoelliptic operators, stochastic partial differential equations in path spaces, such as reaction-diffusion eqaution delay system, Burgers equat

英文关键词： Functional inequalities；Stochastic differential equations；Large deviation principle；；