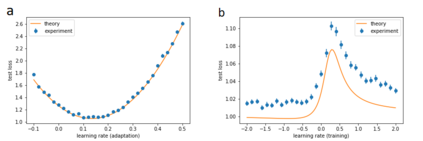
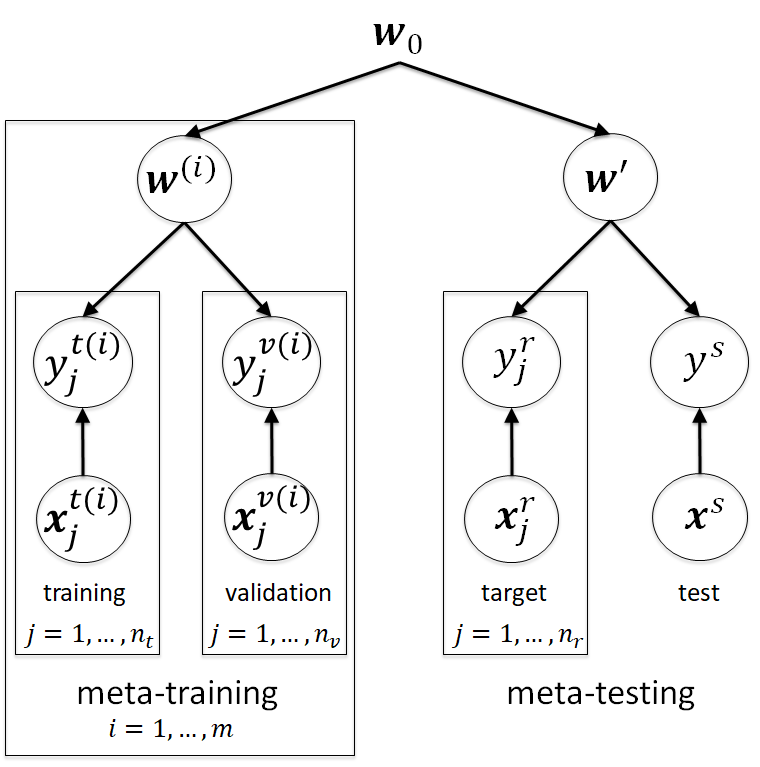
Deep learning models require a large amount of data to perform well. When data is scarce for a target task, we can transfer the knowledge gained by training on similar tasks to quickly learn the target. A successful approach is meta-learning, or "learning to learn" a distribution of tasks, where "learning" is represented by an outer loop, and "to learn" by an inner loop of gradient descent. However, a number of recent empirical studies argue that the inner loop is unnecessary and more simple models work equally well or even better. We study the performance of MAML as a function of the learning rate of the inner loop, where zero learning rate implies that there is no inner loop. Using random matrix theory and exact solutions of linear models, we calculate an algebraic expression for the test loss of MAML applied to mixed linear regression and nonlinear regression with overparameterized models. Surprisingly, while the optimal learning rate for adaptation is positive, we find that the optimal learning rate for training is always negative, a setting that has never been considered before. Therefore, not only does the performance increase by decreasing the learning rate to zero, as suggested by recent work, but it can be increased even further by decreasing the learning rate to negative values. These results help clarify under what circumstances meta-learning performs best.
翻译:深层学习模式需要大量的数据才能很好地发挥作用。 当数据对于目标任务而言缺乏数据时, 我们可以转让通过类似任务培训获得的知识, 快速学习目标。 成功的方法是元学习, 或者“ 学习学习学习” 分配任务, 外环代表“ 学习”, 而“ 学习” 则由梯度下降的内环表示 。 然而, 最近的一些经验研究表明, 内环是不必要的, 更简单的模式同样好甚至更好。 我们研究MAML 的绩效, 因为它是内环学习率的函数, 零学习率意味着没有内环。 使用随机矩阵理论和线性模型的精确解决方案, 我们计算MAML 测试损失的代数表达方式, 用于混合线性回归和不线性回归, 以及过度分解模型的“ 学习 ” 。 令人惊讶的是, 尽管适应的最佳学习率是积极的, 我们发现培训的最佳学习率总是负面的, 一种从未被考虑过的环境。 因此, 我们不仅通过将学习率降低到零, 来提高绩效, 也能够通过最近的工作提出的负面学习结果进一步提高。