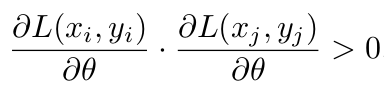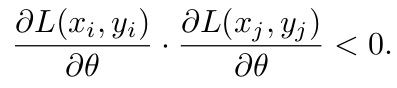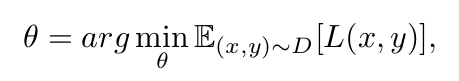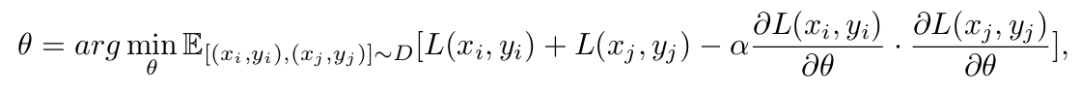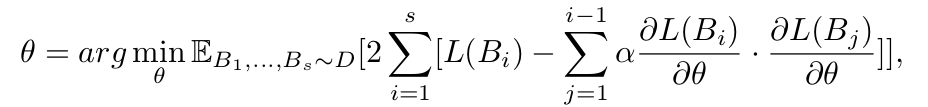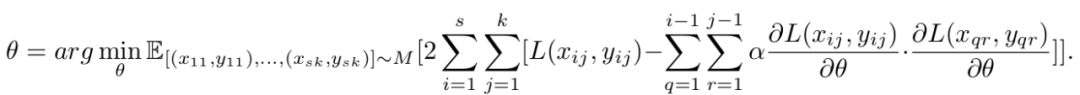灾难性遗忘问题新视角：迁移-干扰平衡

 

  

1. Catastrophic Forgetting and the Stability-Plasticity Dilemma

 

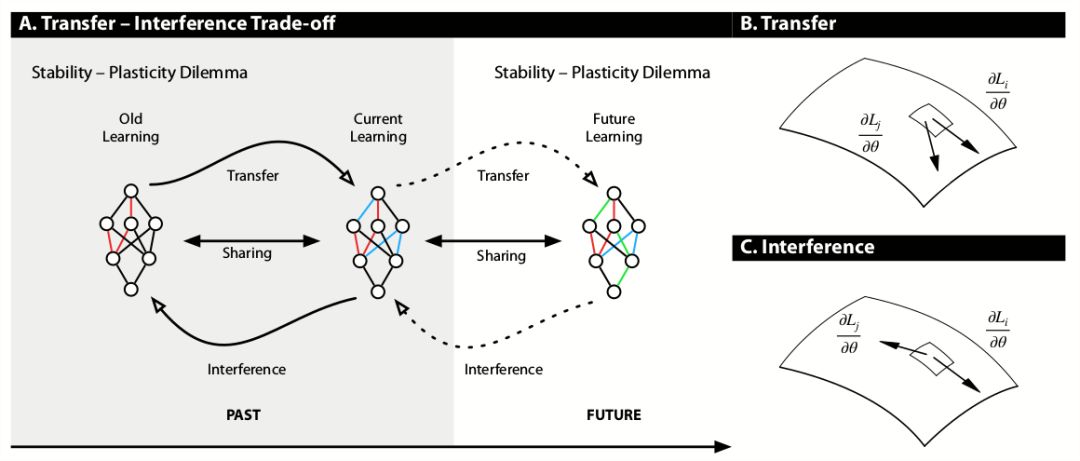
Building neural networks that can learn incrementally without forgetting is one of the existential challenges facing the current generation of deep learning solutions. Over the years, solutions to the continual learning problem have been largely driven by prominent conceptualizations of the issues faced by neural networks. One popular view is catastrophic forgetting (interference), in which the primary concern is the lack of stability in neural networks, and the main solution is to limit the extent of weight sharing across experiences by focusing on preserving past knowledge. Another popular and more complex conceptualization is the stability-plasticity dilemma. In this view, the primary concern is the balance between network stability (to preserve past knowledge) and plasticity (to rapidly learn the current experience), these techniques focus on balancing limited weight sharing with some mechanism to ensure fast learning. 

 

2. Transfer-interference trade-off

 

At an instant in time with parameters θ and loss L, we can define operational measures of transfer and interference between two arbitrary distinct examples (x i , y i ) and (x j , y j ) while training with SGD. Transfer occurs when:

 

This implies that learning example i will without repetition improve performance on example j and vice versa. Interference occurs when:

Here, in contrast, learning example i will lead to unlearning (i.e. forgetting) of example j and vice versa. There is weight sharing between i and j when they are learned using an overlapping set of parameters. So, potential for transfer is maximized when weight sharing is maximized while potential for interference is minimized when weight sharing is minimized.

 

The transfer-interference trade-off presents a novel perspective on the goal of gradient alignment for the continual learning problem.

A) The stability-plasticity dilemma considers plasticity with respect to the current learning and how it degrades old learning. The transfer-interference trade-off considers the stability-plasticity dilemma and its dependence on weight sharing in both forward and backward directions. This symmetric view is crucial as solutions that purely focus on reducing the degree of weight-sharing are unlikely to produce transfer in the future.

B) A depiction of transfer in weight space.

C) A depiction of interference in weight space.

 

The key difference in perspective with past conceptualizations of continual learning is that we are not just concerned with current transfer and interference with respect to past examples, but also with the dynamics of transfer and interference moving forward as we learn. This new view of the problem leads to a natural meta-learning perspective on continual learning: we would like to learn to modify our learning to affect the dynamics of transfer and interference in a general sense.

 

To the extent that our meta-learning into the future generalizes, this should make it easier for our model to perform continual learning in non-stationary settings. We achieve this by building off past work on experience replay algorithm that combines experience replay with optimization based meta-learning.

 

3. Meta-Experience Replay (MER)

 

In typical offline supervised learning, we can express our optimization objective over the stationary
distribution of x, y pairs within the dataset D:

where L is the loss function, which can be selected to fit the problem. If we would like to maximize transfer and minimize interference, we can imagine it would be useful to add an auxiliary loss to the objective to bias the learning process in that direction.

where (x i , y i ) and (x j , y j ) are randomly sampled unique data points. If we could maximize the dot products between gradients at these different points, it would directly encourage the network to share parameters where gradient directions align and keep parameters separate where interference is caused by gradients in opposite directions.

 

However, there are multiple problems that must be addressed to implement this kind of learning process in practice. The first problem is that continual learning deals with learning over a non-stationary stream of data. We address this by implementing an experience replay module that augments online learning so that we can approximately optimize over the stationary distribution of all examples seen so far.

Another practical problem is that the gradients of this loss depend on the second derivative of the loss function, which is expensive to compute. We address this by indirectly approximating the objective to a first order Taylor expansion using a meta-learning algorithm with minimal computational overhead.

 

In this work, we modify the Reptile algorithm ( a state-of-the-art meta-learning model created by OpenAI ) to properly integrate it with an experience replay module, facilitating continual learning while maximizing transfer and minimizing interference.

Reptile objective:

MER objective:

MER maintains an experience replay style memory M with reservoir sampling and at each time step draws s batches including k − 1 random samples from the buffer to be trained alongside the current example. Each of the k examples within each batch is treated as its own Reptile batch of size 1 with an inner loop Reptile meta-update after that batch is processed. We then apply the Reptile meta-update again in an outer loop across the s batches.

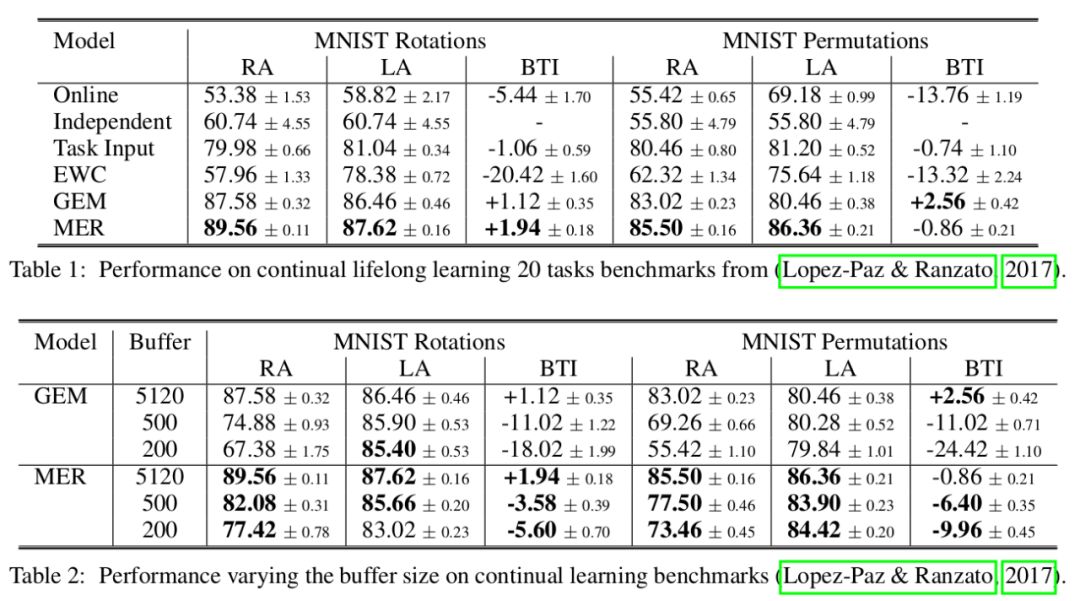
4. Evaluations

 

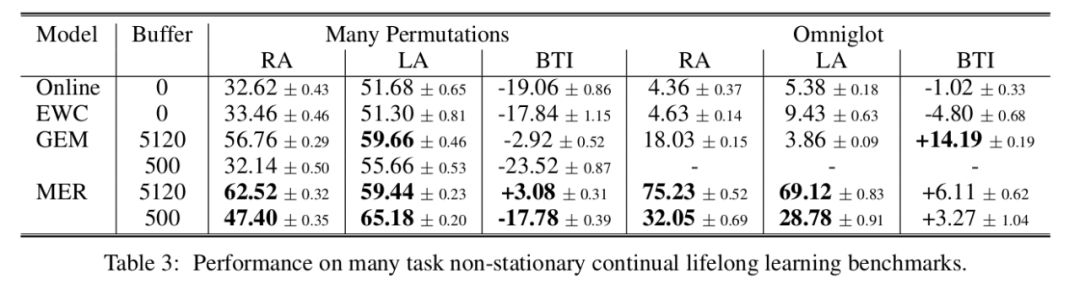
To test the efficacy of MER we compare it to relevant baselines for continual learning of many supervised tasks:

• Online: represents online learning performance of a model trained straightforwardly one example at a time on the incoming non-stationary training data by simply applying SGD.
• Independent: an independent predictor per task with less hidden units proportional to the number of tasks. When useful, it can be initialized by cloning the last predictor.
• Task Input: has the same architecture as Online, but with a dedicated input layer per task.
• EWC: Elastic Weight Consolidation (EWC) is an algorithm that modifies online learning where the loss is regularized to avoid catastrophic forgetting.
• GEM: Gradient Episodic Memory (GEM)  is an approach for making efficient use of episodic storage by following gradients on incoming examples to the maximum extent while altering them so that they do not interfere with past memories.

 

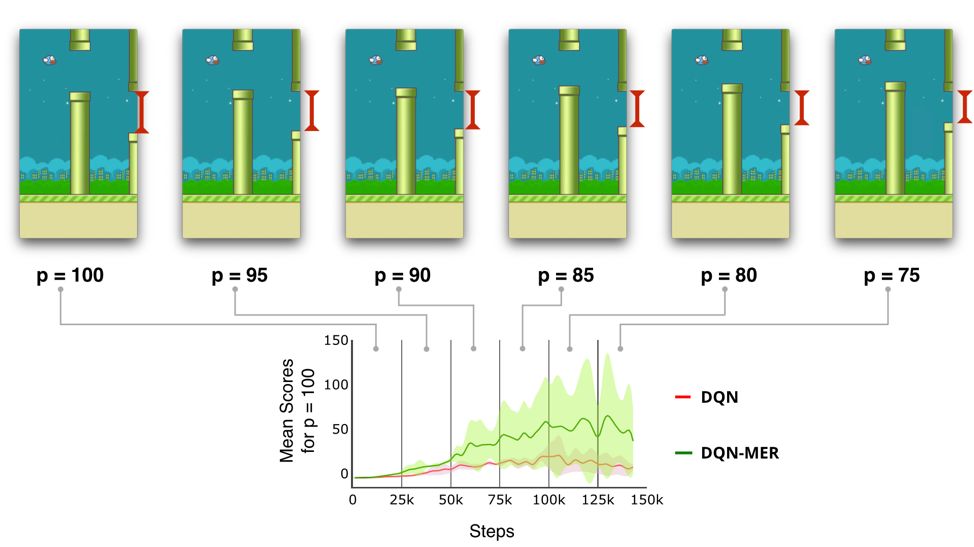
We considered the evaluation of MER in a continual reinforcement learning setting where the environment is highly non-stationary. Specifically, we used Catcher and Flappy Bird. In the case of Flappy Brid, MER was trained to navigate through pipes while making the pipe gap the bird needs to get through smaller and smaller gaps as the game progresses. This environment results particularly challenging to achieve continual reinforcement learning give the sudden changes to the dynamics of gameplay that really tests the agent’s ability to detect changes in the environment without supervision. 

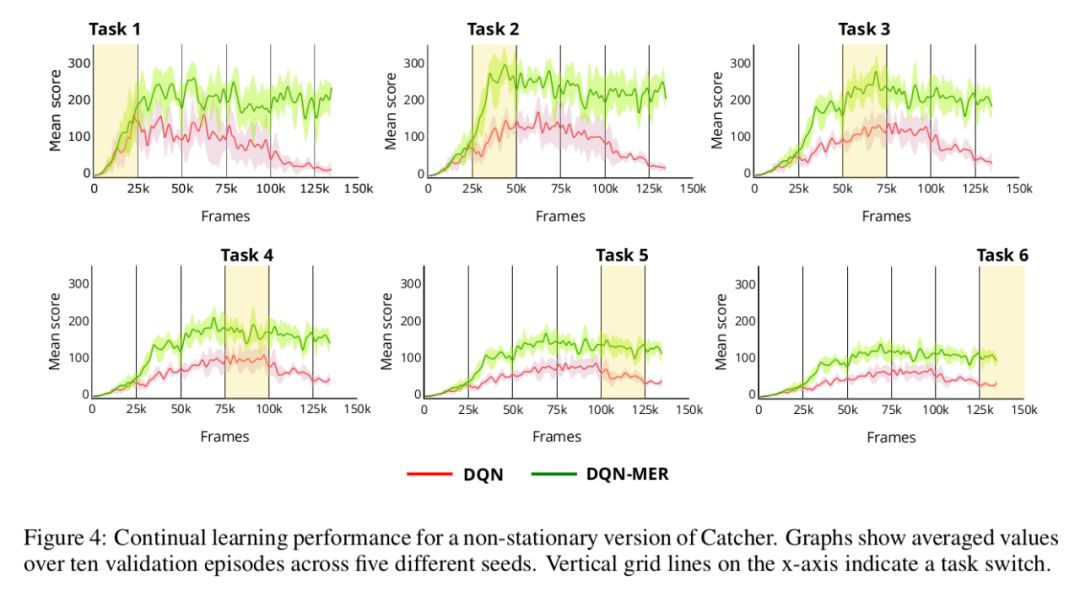
In Catcher, we then obtain different tasks by incrementally increasing the pellet velocity a total of 5 times during training. In the experiments MER outperform standard DQN models as shown in the following figure:

 

Code available at https://github.com/mattriemer/mer.