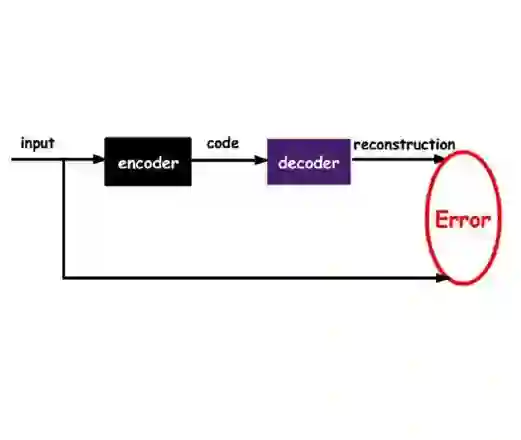
Autoencoders have demonstrated remarkable success in learning low-dimensional latent features of high-dimensional data across various applications. Assuming that data are sampled near a low-dimensional manifold, we employ chart autoencoders, which encode data into low-dimensional latent features on a collection of charts, preserving the topology and geometry of the data manifold. Our paper establishes statistical guarantees on the generalization error of chart autoencoders, and we demonstrate their denoising capabilities by considering $n$ noisy training samples, along with their noise-free counterparts, on a $d$-dimensional manifold. By training autoencoders, we show that chart autoencoders can effectively denoise the input data with normal noise. We prove that, under proper network architectures, chart autoencoders achieve a squared generalization error in the order of $\displaystyle n^{-\frac{2}{d+2}}\log^4 n$, which depends on the intrinsic dimension of the manifold and only weakly depends on the ambient dimension and noise level. We further extend our theory on data with noise containing both normal and tangential components, where chart autoencoders still exhibit a denoising effect for the normal component. As a special case, our theory also applies to classical autoencoders, as long as the data manifold has a global parametrization. Our results provide a solid theoretical foundation for the effectiveness of autoencoders, which is further validated through several numerical experiments.
翻译:自动编码器在各种应用中表现出了学习高维数据的低维潜在特征的显着成功。假设数据在低维流形附近采样,我们采用图表自动编码器,在一组图表上将数据编码为低维潜在特征,保持数据流形的拓扑和几何结构。我们的论文对图表自动编码器的广义误差进行了统计保证,并通过考虑具有$n$个含噪训练样本及其无噪声对应项的$d$维流形上的正常噪声,展示了它们的去噪能力。通过训练自动编码器,我们展示了图表自动编码器可以有效去噪输入数据,并证明在适当的网络结构下,图表自动编码器可以实现二次广义误差,其次数为$\displaystyle n^{-\frac{2}{d+2}}\log^4 n$,它依赖于流形的内在维数,并且仅轻微依赖于环境维度和噪声水平。我们进一步扩展了关于包含正常和切向分量的噪声数据的理论,图表自动编码器仍然展现正常分量的去噪效果。作为一个特殊情况,我们的理论也适用于经典的自动编码器,只要数据流形具有全局参数化。我们的结果为自动编码器的有效性提供了坚实的理论基础,这一点通过几个数值实验进一步验证。