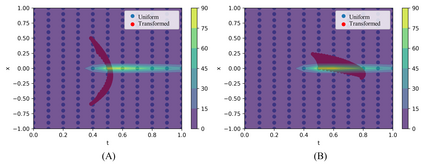
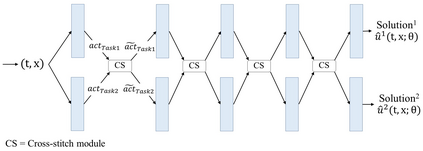
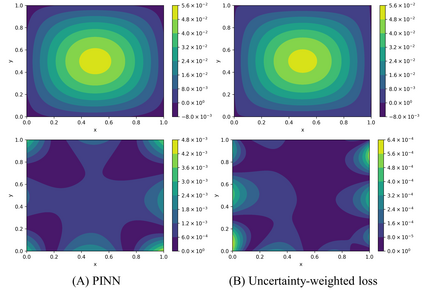
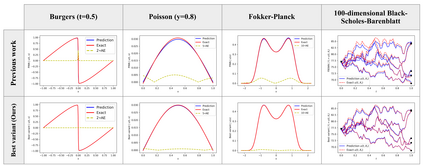
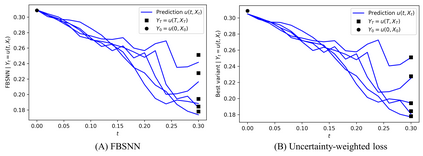
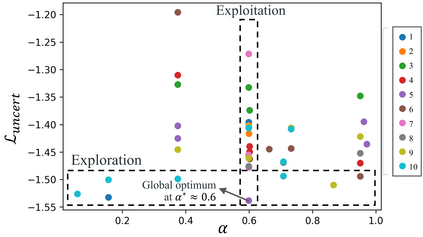
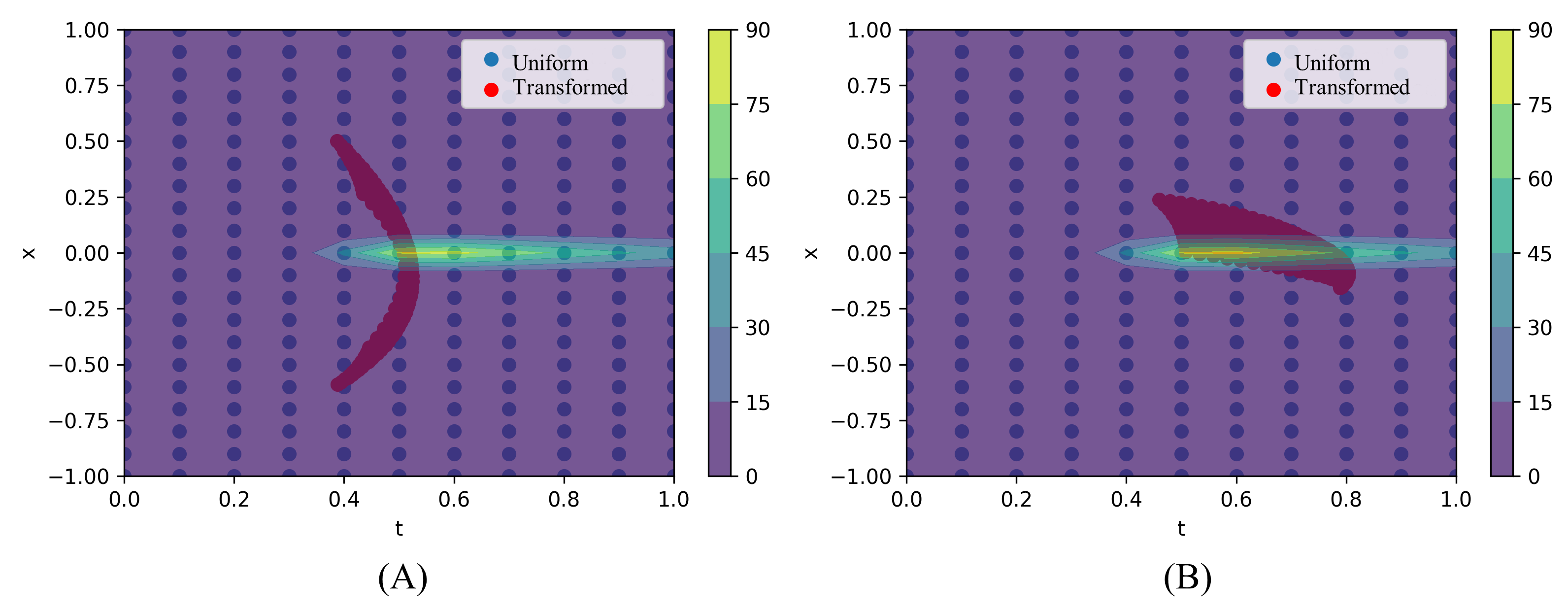
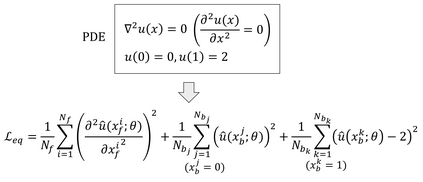Recently, researchers have utilized neural networks to accurately solve partial differential equations (PDEs), enabling the mesh-free method for scientific computation. Unfortunately, the network performance drops when encountering a high nonlinearity domain. To improve the generalizability, we introduce the novel approach of employing multi-task learning techniques, the uncertainty-weighting loss and the gradients surgery, in the context of learning PDE solutions. The multi-task scheme exploits the benefits of learning shared representations, controlled by cross-stitch modules, between multiple related PDEs, which are obtainable by varying the PDE parameterization coefficients, to generalize better on the original PDE. Encouraging the network pay closer attention to the high nonlinearity domain regions that are more challenging to learn, we also propose adversarial training for generating supplementary high-loss samples, similarly distributed to the original training distribution. In the experiments, our proposed methods are found to be effective and reduce the error on the unseen data points as compared to the previous approaches in various PDE examples, including high-dimensional stochastic PDEs.
翻译:最近,研究人员利用神经网络准确解决部分差异方程式(PDEs),使无网状科学计算方法得以实现。不幸的是,当遇到高非线性域时,网络性能下降。为了改进一般性,我们在学习PDE解决方案的背景下,引入了采用多任务学习技术、不确定性加权损失和梯度外科手术的新方法。多任务计划利用了学习由交叉切入模块控制的多相关PDEs之间共享演示的优势,而多相关PDEs可以通过不同的PDE参数化系数获得,从而更好地普及原PDE。鼓励网络更密切地关注更难于学习的高非线性域域域区。我们还建议进行对抗性培训,以产生补充性高损失样本,类似地分配给最初的培训分布。在实验中,我们提出的方法被认为有效,并减少了与以往各种PDE实例中的方法相比,包括高维度随机PDEPDE中的数据点的错误。