Design-based theory for cluster rerandomization

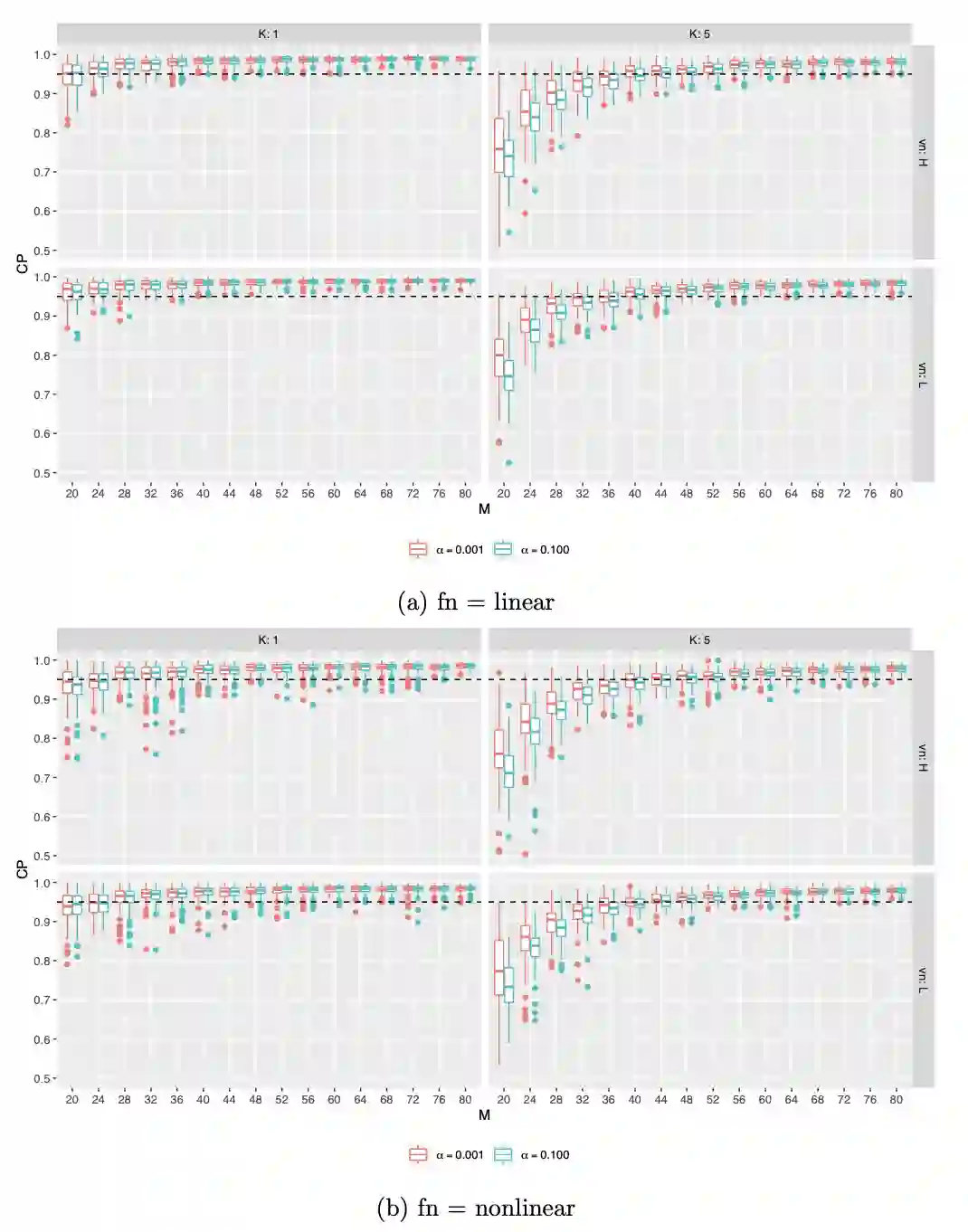
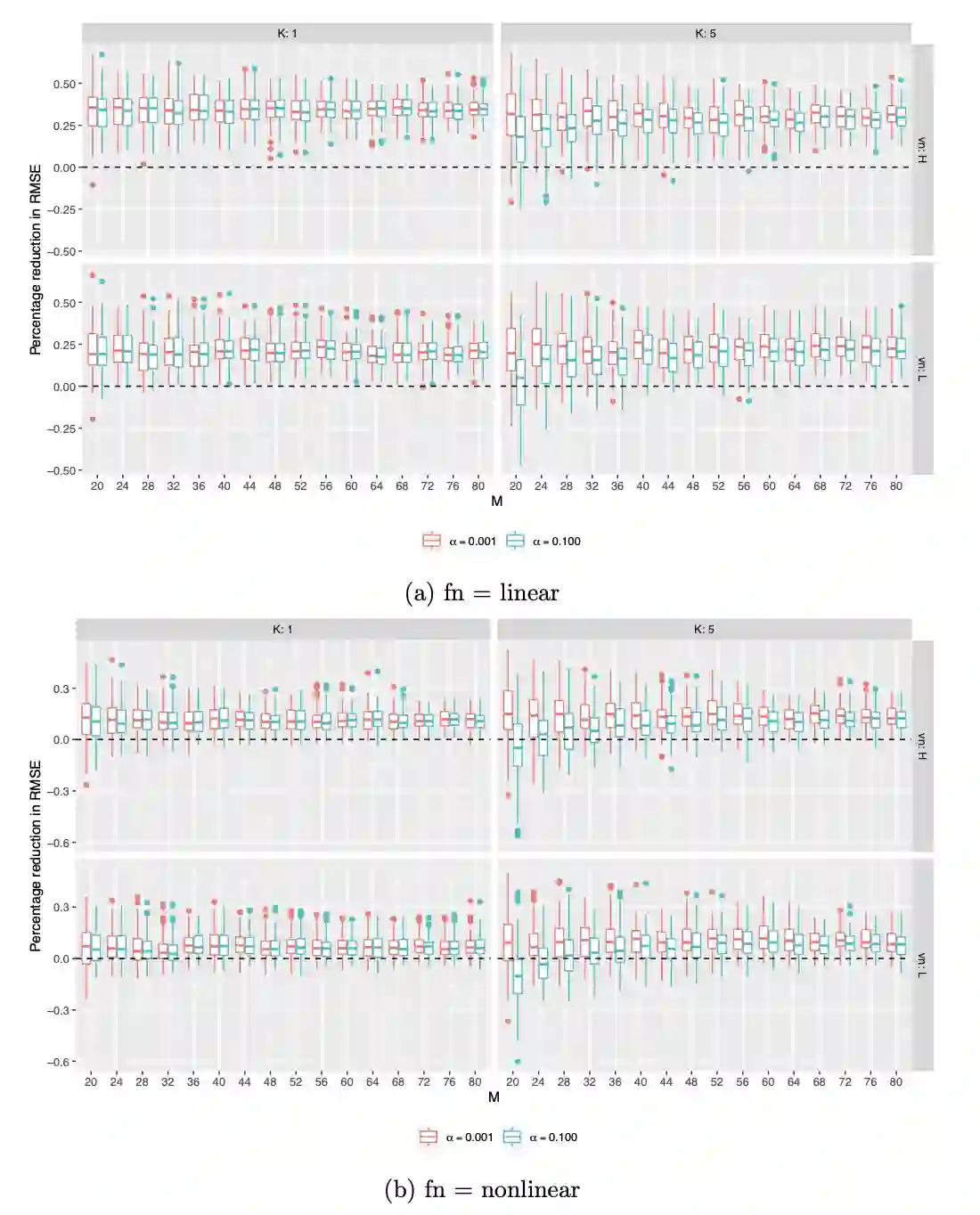
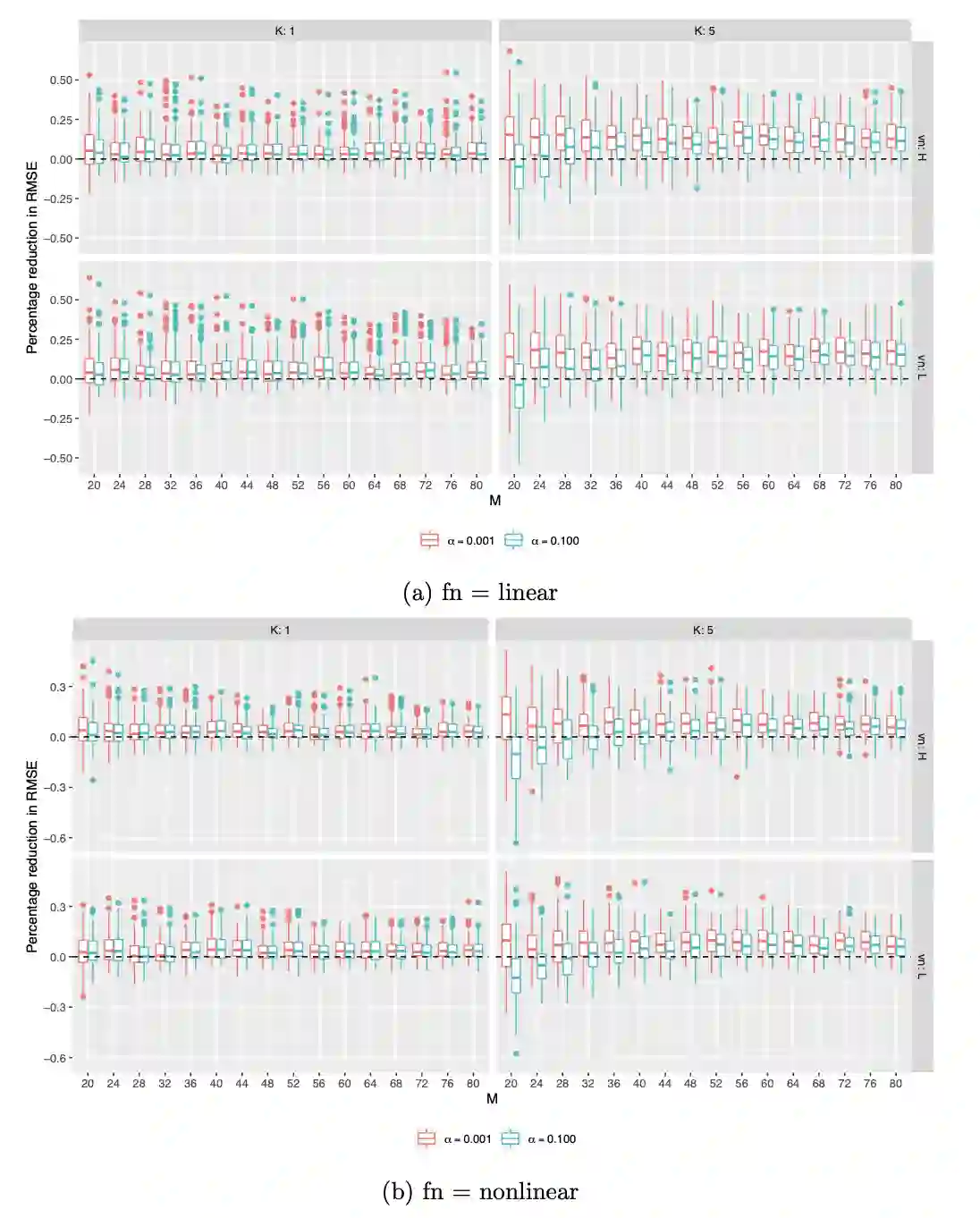
Complete randomization balances covariates on average, but covariate imbalance often exists in finite samples. Rerandomization can ensure covariate balance in the realized experiment by discarding the undesired treatment assignments. Many field experiments in public health and social sciences assign the treatment at the cluster level due to logistical constraints or policy considerations. Moreover, they are frequently combined with rerandomization in the design stage. We refer to cluster rerandomization as a cluster-randomized experiment compounded with rerandomization to balance covariates at the individual or cluster level. Existing asymptotic theory can only deal with rerandomization with treatments assigned at the individual level, leaving that for cluster rerandomization an open problem. To fill the gap, we provide a design-based theory for cluster rerandomization. Moreover, we compare two cluster rerandomization schemes that use prior information on the importance of the covariates: one based on the weighted Euclidean distance and the other based on the Mahalanobis distance with tiers of covariates. We demonstrate that the former dominates the latter with optimal weights and orthogonalized covariates. Last but not least, we discuss the role of covariate adjustment in the analysis stage and recommend covariate-adjusted procedures that can be conveniently implemented by least squares with the associated robust standard errors.