PKLM: A flexible MCAR test using Classification

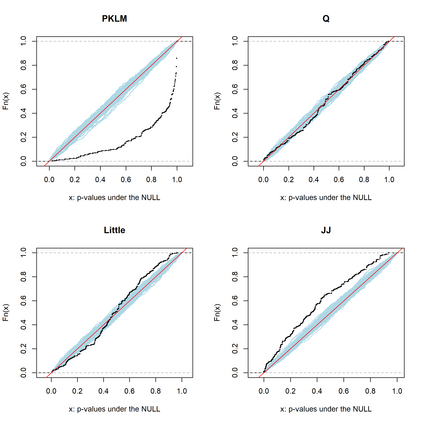
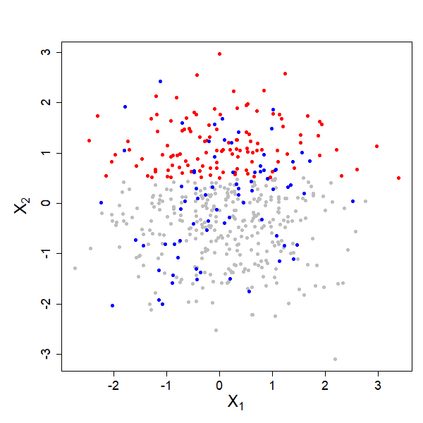
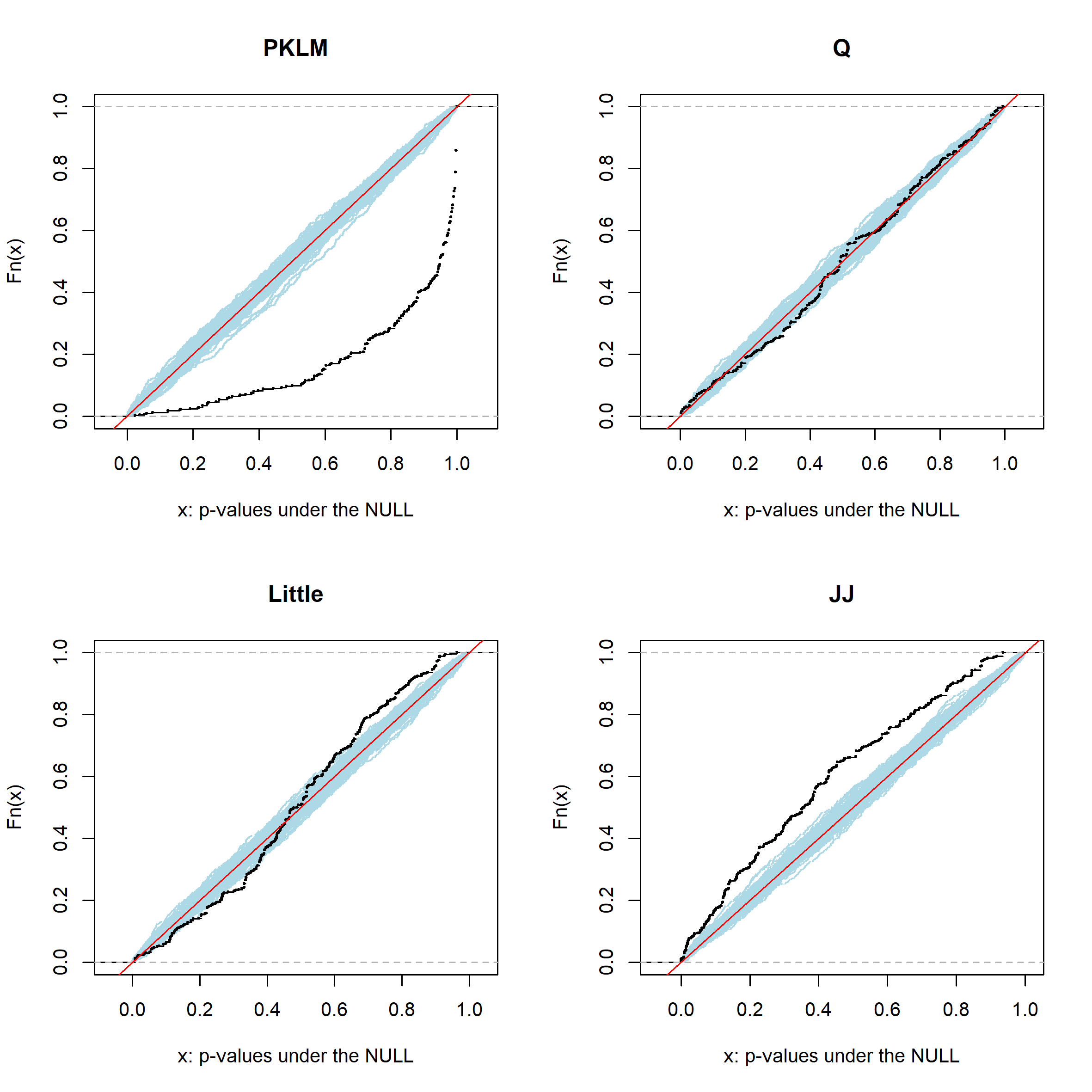
We develop a fully non-parametric, fast, easy-to-use, and powerful test for the missing completely at random (MCAR) assumption on the missingness mechanism of a data set. The test compares distributions of different missing patterns on random projections in the variable space of the data. The distributional differences are measured with the Kullback-Leibler Divergence, using probability Random Forests. We thus refer to it as "Projected Kullback-Leibler MCAR" (PKLM) test. The use of random projections makes it applicable even if very little or no fully observed observations are available or if the number of dimensions is large. An efficient permutation approach guarantees the level for any finite sample size, resolving a major shortcoming of most other available tests. Moreover, the test can be used on both discrete and continuous data. We show empirically on a range of simulated data distributions and real data sets that our test has consistently high power and is able to avoid inflated type I errors. Finally, we provide an R-package \texttt{PKLMtest} with an implementation of our test.