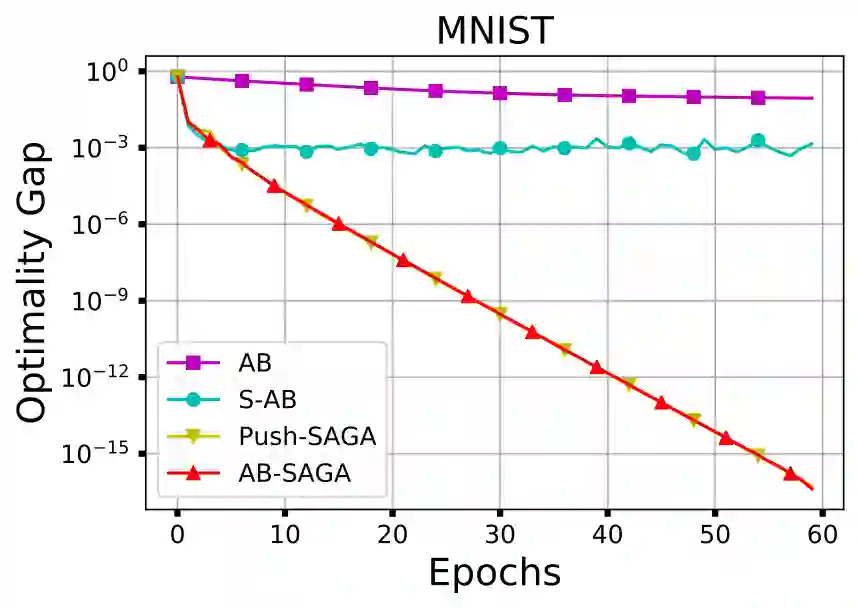
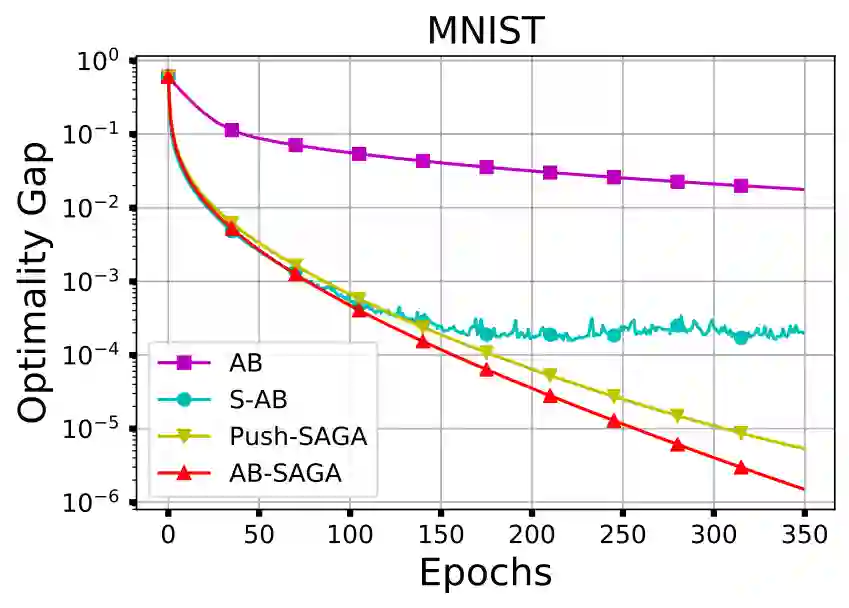
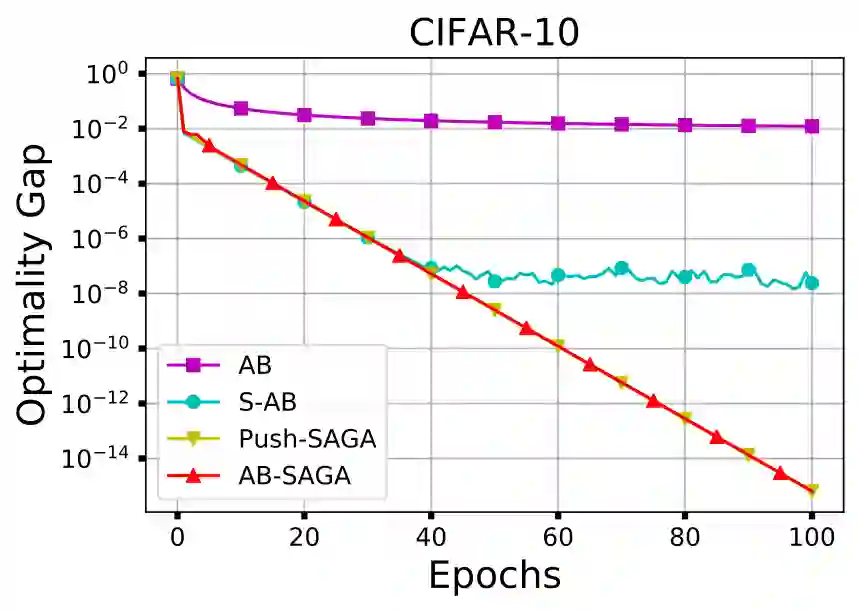
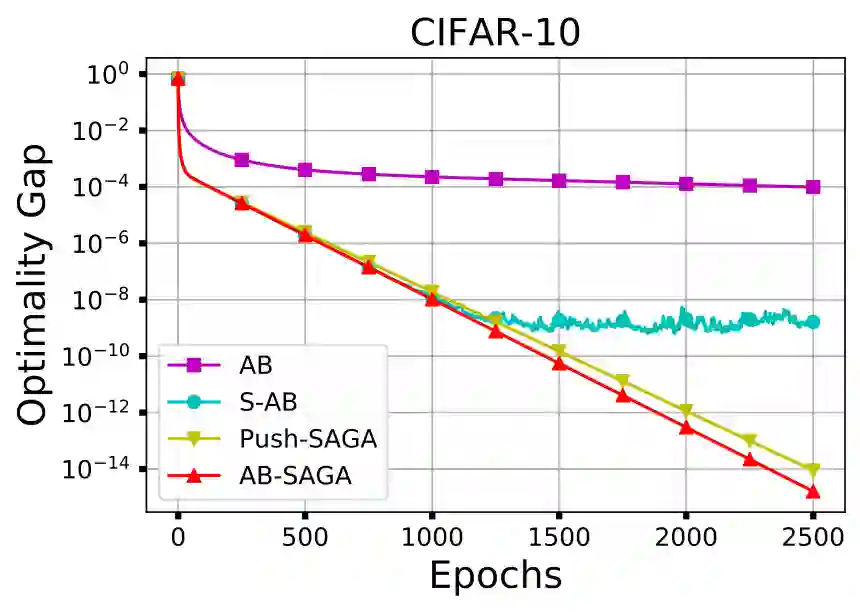
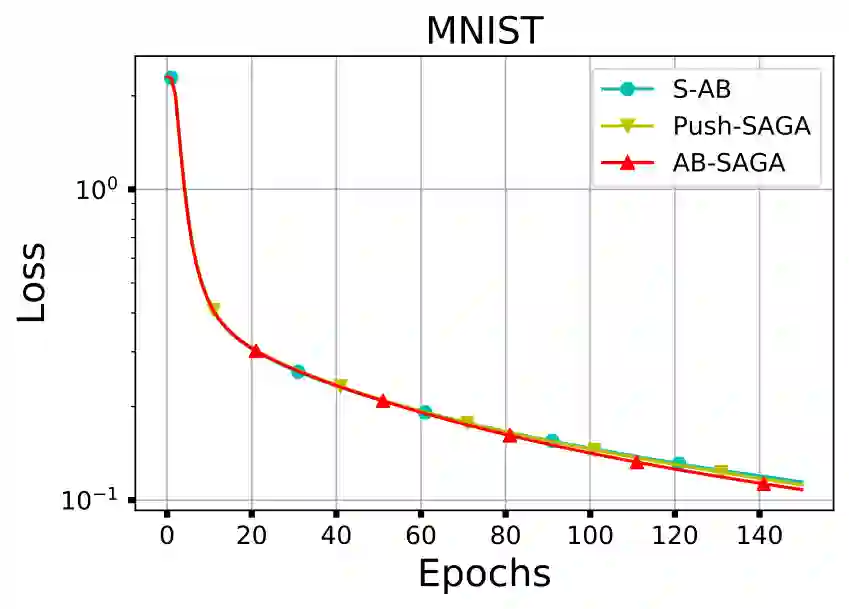
This paper proposes AB-SAGA, a first-order distributed stochastic optimization method to minimize a finite-sum of smooth and strongly convex functions distributed over an arbitrary directed graph. AB-SAGA removes the uncertainty caused by the stochastic gradients using a node-level variance reduction and subsequently employs network-level gradient tracking to address the data dissimilarity across the nodes. Unlike existing methods that use the nonlinear push-sum correction to cancel the imbalance caused by the directed communication, the consensus updates in AB-SAGA are linear and uses both row and column stochastic weights. We show that for a constant step-size, AB-SAGA converges linearly to the global optimal. We quantify the directed nature of the underlying graph using an explicit directivity constant and characterize the regimes in which AB-SAGA achieves a linear speed-up over its centralized counterpart. Numerical experiments illustrate the convergence of AB-SAGA for strongly convex and nonconvex problems.
翻译:本文建议采用AB-SAGA(AB-SAGA)这一第一级分布式随机优化法,以最大限度地减少在任意方向图上分布的光滑和强烈凝固功能的有限和微积分。AB-SAGA(AB-SAGA)通过节点差异减少来消除由随机梯度梯度梯度造成的不确定性,并随后使用网络级梯度跟踪来解决各节点的数据差异。与使用非线性推力和校正来消除直接通信造成的不平衡的现有方法不同,AB-SAGA(AB-SAGA)中的协商一致更新是线性更新,同时使用行和列相容重量。我们表明,对于恒定的步度,AB-SAGA(AB-SAGA)将线性图的直线性与全球最佳一致。我们用明确的直率常数来量化底图的直线性,并描述AB-SAGAGA(A)在集中对应方方面达到线性速度的系统。