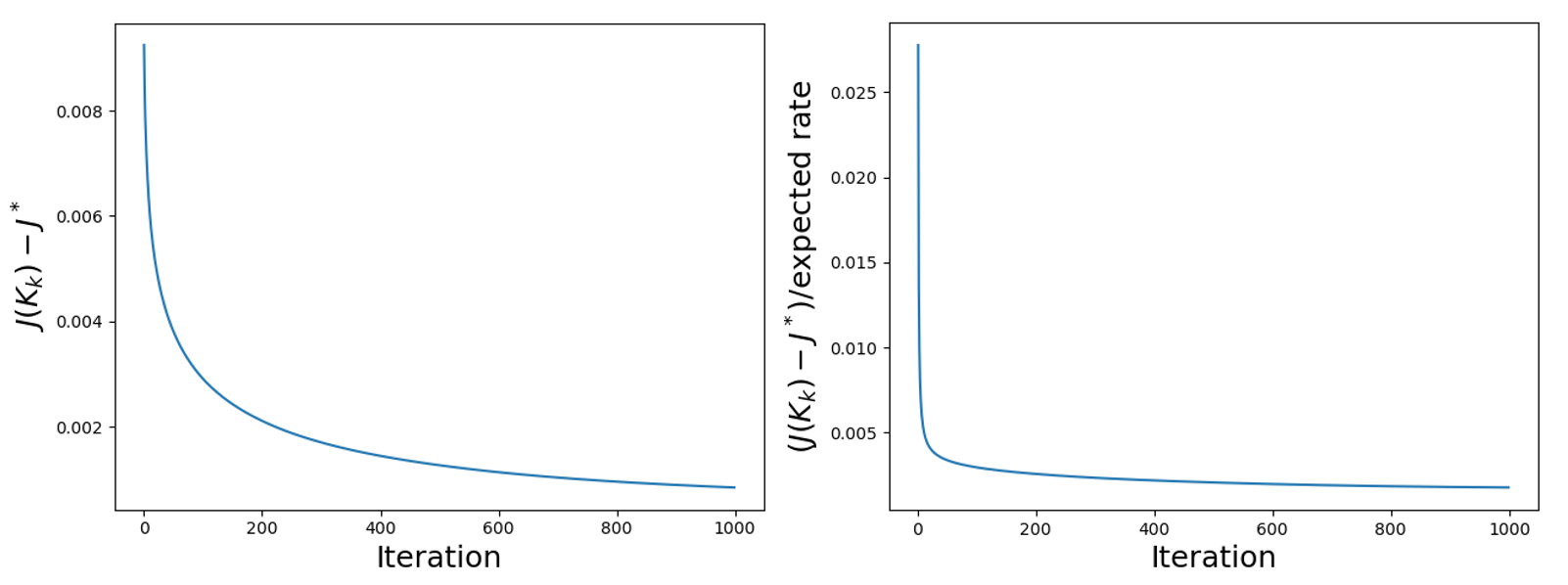
We study a new two-time-scale stochastic gradient method for solving optimization problems, where the gradients are computed with the aid of an auxiliary variable under samples generated by time-varying Markov random processes parameterized by the underlying optimization variable. These time-varying samples make gradient directions in our update biased and dependent, which can potentially lead to the divergence of the iterates. In our two-time-scale approach, one scale is to estimate the true gradient from these samples, which is then used to update the estimate of the optimal solution. While these two iterates are implemented simultaneously, the former is updated "faster" (using bigger step sizes) than the latter (using smaller step sizes). Our first contribution is to characterize the finite-time complexity of the proposed two-time-scale stochastic gradient method. In particular, we provide explicit formulas for the convergence rates of this method under different structural assumptions, namely, strong convexity, convexity, the Polyak-Lojasiewicz condition, and general non-convexity. We apply our framework to two problems in control and reinforcement learning. First, we look at the standard online actor-critic algorithm over finite state and action spaces and derive a convergence rate of O(k^(-2/5)), which recovers the best known rate derived specifically for this problem. Second, we study an online actor-critic algorithm for the linear-quadratic regulator and show that a convergence rate of O(k^(-2/3)) is achieved. This is the first time such a result is known in the literature. Finally, we support our theoretical analysis with numerical simulations where the convergence rates are visualized.
翻译:我们研究一种新的双时间尺度的梯度方法,以解决优化问题,在这个方法中,梯度是用一个辅助变量的辅助变量在由时间变化的Markov随机过程产生的样本中根据基本优化变量参数产生的样本中计算出来的。这些时间变化的样本使我们更新时的梯度方向有偏差和依赖性,这有可能导致迭代的偏差。在我们的双时间尺度方法中,一个尺度是估计这些样品的真实梯度,然后用来更新最佳解决方案的估计数。这两个迭代国同时实施,前者是更新“加速”(使用较大的步数),前者是更新“加速”(使用较大的步数)而不是后者(使用较小的步数 )。我们的第一个贡献是描述拟议两次时间变化的梯度,这可能会导致迭代国之间的差异。在我们不同的结构假设下,即强烈的粘结度、粘结度、Polyak-Lojasiewiz条件和一般非cionxity。我们用我们的框架更新了“加速”的“加速度(使用更大的步数 ) 。我们用两个框架在控制和强化O-2 递增缩递增的轨率方法中,我们先用一个已知的动作分析中,我们用的是已知的精确速度来显示一个已知的精确速度。我们所了解到的轨道速度。我们所了解到的轨道的轨道的精确率。我们先是用来分析。我们所了解到的第二一个已知的轨道的轨道的精确速度。我们所了解到的精确速度。