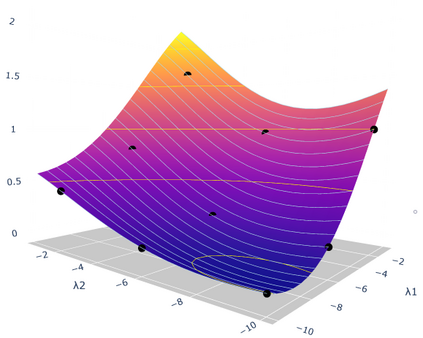
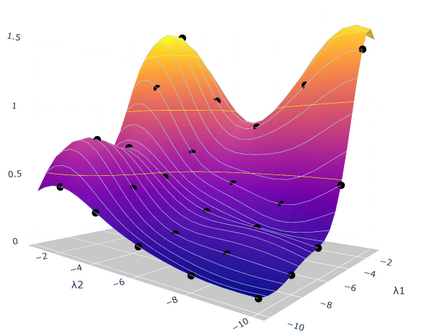
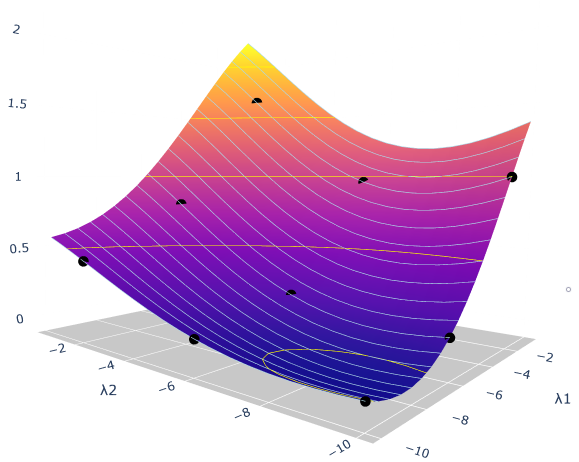
Hyperparameter optimization in machine learning is often achieved using naive techniques that only lead to an approximate set of hyperparameters. Although techniques such as Bayesian optimization perform an intelligent search on a given domain of hyperparameters, it does not guarantee an optimal solution. A major drawback of most of these approaches is an exponential increase of their search domain with number of hyperparameters, increasing the computational cost and making the approaches slow. The hyperparameter optimization problem is inherently a bilevel optimization task, and some studies have attempted bilevel solution methodologies for solving this problem. However, these studies assume a unique set of model weights that minimize the training loss, which is generally violated by deep learning architectures. This paper discusses a gradient-based bilevel method addressing these drawbacks for solving the hyperparameter optimization problem. The proposed method can handle continuous hyperparameters for which we have chosen the regularization hyperparameter in our experiments. The method guarantees convergence to the set of optimal hyperparameters that this study has theoretically proven. The idea is based on approximating the lower-level optimal value function using Gaussian process regression. As a result, the bilevel problem is reduced to a single level constrained optimization task that is solved using the augmented Lagrangian method. We have performed an extensive computational study on the MNIST and CIFAR-10 datasets on multi-layer perceptron and LeNet architectures that confirms the efficiency of the proposed method. A comparative study against grid search, random search, Bayesian optimization, and HyberBand method on various hyperparameter problems shows that the proposed algorithm converges with lower computation and leads to models that generalize better on the testing set.
翻译:机器学习中的超光量计优化通常使用天真的技术来实现,这些技术只能导致一套近似超光度计。虽然贝叶西亚优化等技术对超光度计的某一领域进行智能搜索,但并不能保证最佳解决办法。大多数这些方法的主要缺点是其搜索域与超光度计数成指数式增长,增加了计算成本,使方法减慢。超光度优化问题本身就是一个双级优化任务,有些研究尝试了双级解决方案方法来解决这个问题。然而,这些研究假设了一套独特的模型重量,可以最大限度地减少培训损失,而这种培训损失通常被深层学习结构所破坏。本文讨论了一种基于梯度的双级方法来解决超光度优化问题。拟议方法可以处理连续超光度的超光度计量,为此我们选择了在实验中使用的正规超光度计计。该方法可以保证与本研究已经理论上证明的最佳超光度超光值计组合相趋一致。该方法基于对低水平的最佳值功能进行对低水平的优化值功能,而深度的测试通常为深度学习结构的精确度, 也通过一个测试方法来测量一个测试。