导语
观点动力学(Opinion Dynamics)聚焦于个体初始观点(通常以连续或离散变量表征)如何通过特定交互规则(如同群影响、权威服从)调整,并最终涌现出群体层面的观点分布特征(如共识收敛、多阵营分化、极化加剧等),其核心目标是揭示观点演化的内在规律,为理解社会舆论传播、群体决策形成等现实问题提供可量化的理论工具。基于主体建模(Agent-based Modeling,ABM)为其提供了工具载体。作为一种自下而上的建模思维与方法,它既能通过具有自主属性的 Agent 刻画个体属性,又能定义主体间的交互规则,模拟系统动态演化。其将个体的观点属性、互动模式等抽象为可计算规则,定义非线性复杂适应系统环境,使观点的分化、同化等过程在 “人工社会” 中具象呈现,进而清晰揭示群体观点从微观互动到宏观演化的内在逻辑。
**
**
**本文为你梳理了基于多主体进行观点动力学建模的思维脉络:以理解群体交互对个体观点的重要影响为起点,从现实情境中提炼主体属性、交互规则、社会环境三类ABM建模核心要素,接着以DeGroot、Friedkin-Johnsen模型为例,展开符合初学者探索逻辑的ABM实操讲解。最后,说明在更广泛的科学研究问题中采用ABM方法的适用性。 **
**
**
**
关键词:基于主体建模、非线性、复杂适应系统、观点动力学、自下而上建模********************************
赵沐天丨作者
王朝会|审校
ABM 是一种思维方式,而不仅仅是一门技术。 —— Eric Bonabeau[1]
1. 理解交互对观点形成的重要影响
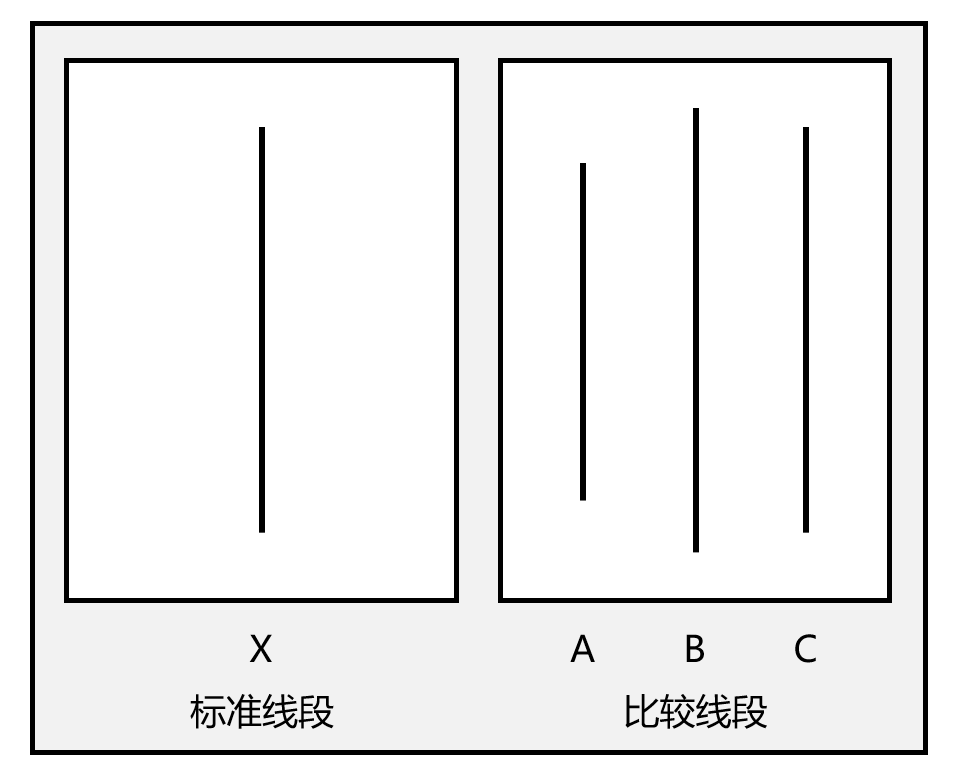
1951年的一天,所罗门·阿希(Solomon E. Asch)开展了一场社会心理学实验。实验开始时,参与者被带入一个房间,被告知这是一场关于“视觉感知”的研究。房间里坐着七位“被试”,但真正的被试者并不知道,其余六人其实是实验助手。研究人员拿出卡片,要求所有人依次指出右边卡片上与左边线段等长的线段。前两轮测试,所有人都给出了正确答案。
线段判断实验 从第三轮测试开始,当研究人员再次拿出卡片,助手们开始故意给出错误答案。在最后进行选择的真正被试者,面对群体一致的“错误”,会如何抉择呢?实验结果出乎意料:在12轮关键测试中,约75%的参与者至少有一次随大流给出错误答案。阿希在1951、1956和1958年多次重复了这项系列实验。结果表明:实验全程始终坚持独立判断的人,仅占总人数的25%-35%。
阿希实验揭示了群体交互对个体认知的重要影响:人类的认知并非绝对理性,在群体压力下,我们会不自觉地调整判断,甚至放弃亲眼所见的事实(启示1)。
**
**
接下来,试想如果选择涉及道德抉择,个体是否还会受到群体影响?
1963年,斯坦利·米尔格拉姆(Stanley Milgram)在耶鲁大学展开实验,意在探究“普通人在权威命令下能在多大程度上违背良心”。研究发现,65% 的普通人会在权威指令下突破道德底线,执行他们认为会造成伤害的行为。
共同地,这两个实验揭示了群体压力的影响:群体影响的力量似乎远超我们的想象。在阿希实验中,个体即便具备独立做出正确判断的能力,仍会在群体压力下选择遵从错误共识。在米尔格拉姆实验中,当权威指令与道德直觉发生冲突时,多数人选择违背内心准则而持续服从权威指令(启示2)。
**
**
不同之处在于,二者的实验环境存在明显差异:阿希实验呈现的是扁平化的同群互动网络,群体成员以平等身份形成共识压力;而米尔格拉姆实验则构建了垂直化的权威层级结构,清晰划分出指令发出者与行为执行者的角色定位(启示3)。
**
**
虽然这些实验结果表明了群体观点对个人的显著影响,但不可忽视的是:在阿希实验中,即便群体压力巨大,但仍有个体坚持独立思考;米尔格拉姆实验亦证实,道德认知越健全的人,越能在权威指令与伦理良知的冲突中保持行为自主性。
基于此,我们可以再次得到三条启示:个体是否选择从众,是多重心理因素综合作用的结果(启示4);“固执观点”的存在,缓冲了群体极化现象(启示5);群体中的个体间存在差异,这种差异构成了社会系统复杂性的微观基础(启示6)。
**
**
群体交互对个体观点的形成具有重要影响。为观察和比较不同情境下的系统演化规律,可借助NetLogo等多主体建模工具,将群体压力、个体差异等现实规则抽象为可计算的模型参数,在 “人工社会” 中模拟观点传播的动态过程,通过可视化结果探明群体影响的内在机制。
上述6条启示已经帮助你自然地理解,为何交互机制、社会环境与主体属性是建模的核心要素:启示 1、2 指向交互机制设计,启示 3 讨论了社会环境的差异性,启示 4-6 则涉及主体属性对动态演化的影响。至此,你具备了基于主体建模方法进行观点动力学建模的基本逻辑认识,即便此前对该领域全然陌生。
2. 用NetLogo实现观点动力学建模
各类揭示群体观点形成机制的社会心理学实验为观点动力学奠定了理论基础。例如勒温的场论、Sherif的光点实验,以及上文提到的阿希线段判断实验和米尔格拉姆服从实验。为辨识社会意识的交互规律,众多观点动力学线性模型作出了各类规则表达[2]。DeGroot模型以邻居观点的加权平均构建交互规则。Friedkin-Johnsen模型在此之上,引入个体对初始观点的坚持程度。Hegselmann-Krause等有界置信模型则设置了观点交互阈值,刻画相似观点间的聚集倾向。选民模型等离散模型,则专注于二元观点的演变。
随着复杂网络理论与统计物理方法的融入,观点动力学被广泛应用于非线性复杂系统与网络结构耦合建模[3-5],以刻画群体观点极化、聚类等复杂现象。采用ABM方法构建观点动力学模型,具有显著契合性和独特价值: * 基于主体建模为为理解复杂性(complexity)问题提供了有效路径。自下而上的建模逻辑能够通过自组织(self-organization)过程产生涌现(emergence)现象,并支持对系统演化过程的动态观测,为解析群体观点的形成机制提供了直观视角。 * 通过对个体互动过程的刻画,基于主体建模将复杂社会场景中的观点交互问题抽象为简化规则,构造复杂适应系统(Complex Adaptive System,CAS),揭示微观行为与宏观现象的内在关联。 * 建模方法能够针对不同情境下的群体观点演化问题展开分析与讨论,实现对问题的理解、定义、量化、可视化与仿真,为多样化现实情境的模拟与预测提供支撑。
如今,数据驱动与多主体建模的融合成为重要发展方向[6,7]。随着深度学习、大模型与网络分析交叉应用的不断深入,有望在舆论趋势预测等实际场景中实现更精准的动态建模。
接下来,我们将以DeGroot和Friedkin-Johnsen这两个经典的观点动力学模型为例,层层拆解现实问题,逐步理解基于Agent的观点动力学建模逻辑,把复杂的社交场景「翻译」成模型里的规则代码!
2.1 实现模型的基本规则
在DeGroot模型中,群体成员在初始状态下持有差异化观点倾向(以连续变量表示)。每次调整观点时,个体都会「完全听周围人的意见」,把别人的想法按信任程度加权平均,再变成自己的新想法。而Friedkin-Johnsen模型在更新个体观点时,保留了一部分「个性态度」,另一部分则是周围人的意见加权平均。
DeGroot 模型可以用来描述现实情境中以群体共识为导向的交流状态。例如,食品安全事件引发舆情传播,信息在社交网络中快速流动,公众形成对事件的共识性判断;在公共卫生知识的普及过程中,社会逐步统一对科学方法的认识;团队成员为推进项目,通过充分交流凝聚执行方案。但是,在社会舆论中,个体带有初始观念、难以完全受到社会环境影响的情境广泛存在。例如,因为品牌忠诚度、消费习惯等属性存在差异,所以不同消费者对品牌营销事件的反应可能有所不同;跨部门协作中,不同团队虽会努力相互配合,却始终关注自身角色利益。为描述该问题,Friedkin-Johnsen模型应运而生,用于表达这些情境里个体保留认知差异,同时又受到群体影响的状态。
第一步,让我们根据DeGroot和Friedkin-Johnsen模型的基本原理,依据交互机制、社会环境与主体属性三个建模要素,将模型思想转化为建模规则。 * 交互机制:在这里,设置每个主体通过交互半径识别周围邻居;使用指数衰减函数计算与邻居的连接强度,采用加权平均规则考虑邻居影响,距离越近权重越高。 * 社会环境规则:设置主体空间内均匀分布,形成空间依赖的交互网络。 * 主体属性:采用连续值(0-1)表示观点倾向(正面-负面)。设置观点越正面,主体颜色越浅;观点越负面,主体颜色越深。根据模型要求,主体观点更新规则为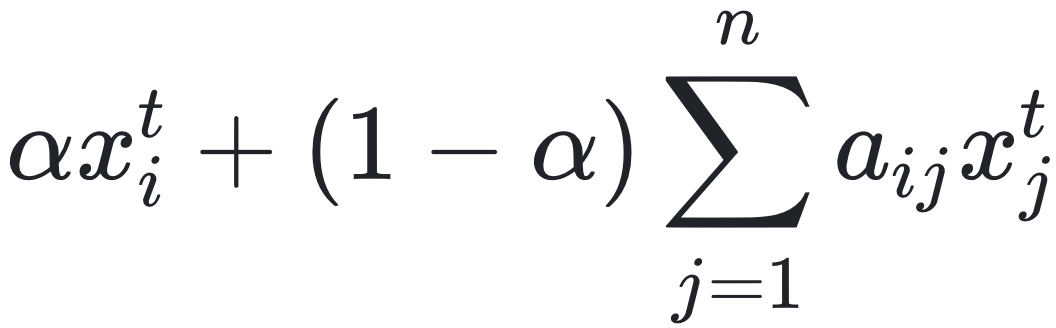
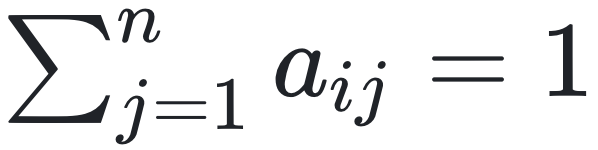
下面是一个完整的NetLogo示例代码(使用NetLogo 6.3.0编写): * *
globals [` num-agents ;; 主体数量`` neighbor-radius ;; 邻居识别半径`` step-counter ;; 时间步计数器``]``
``turtles-own [`` opinion ;; 主体观点 (0-1)`` self-weight ;; 自身权重`` neighbor-weights ;; 邻居及其对应权重的关联列表``]``
``to setup`` clear-all`` reset-ticks``
`` ;; 参数初始化`` set num-agents 200`` set neighbor-radius 5`` set step-counter 0``
`` ;; 创建主体(均匀分布)`` create-turtles num-agents [`` set shape "circle"`` set size 1.5``
`` ;; 随机位置与观点`` setxy random-xcor random-ycor`` set opinion random-float 1 ;; 均匀分布的初始观点`` update-weights ;; 初始化权重`` update-color ;; 根据观点设置颜色`` ]``end``
``to update-weights`` ;; 清空并重新计算所有权重`` set self-weight 0.2 ;; 自身权重`` set neighbor-weights [] ;; 邻居权重列表``
`` ;; 获取邻居代理集(排除自身)`` let my-neighbors other turtles in-radius neighbor-radius`` let neighbor-total-weight 0`` let neighbor-list sort my-neighbors``
`` ;; 计算邻居权重(不包括自身)`` foreach neighbor-list [ n ->`` let dist distance n`` let w exp (-5 * dist) ;; 指数衰减函数计算权重`` set neighbor-weights lput (list n w) neighbor-weights`` set neighbor-total-weight neighbor-total-weight + w`` ]``
`` ;; 归一化邻居权重(使邻居权重总和为1)`` let normalized-neighbor-weights []`` foreach neighbor-weights [ pair ->`` let neighbor item 0 pair`` let weight item 1 pair`` set normalized-neighbor-weights lput (list neighbor (weight / neighbor-total-weight)) normalized-neighbor-weights`` ]``
`` set neighbor-weights normalized-neighbor-weights``end``
``to update-color`` ;; 观点越正向(接近1),颜色接近浅蓝色`` ;; 观点越负面(接近0),颜色接近深蓝色`` set color scale-color blue opinion 0 1``end``
``to go`` if not any? turtles [ stop ]``
`` ;; 更新权重并计算新观点`` ask turtles [`` update-weights`` let new-op 0``
`` ;; 自身观点贡献`` set new-op new-op + self-weight * opinion``
`` ;; 所有邻居观点的加权贡献`` let neighbor-influence 0`` foreach neighbor-weights [ pair ->`` let neighbor item 0 pair`` let weight item 1 pair`` set neighbor-influence neighbor-influence + weight * [opinion] of neighbor`` ]`` set new-op new-op + (1 - self-weight) * neighbor-influence``
`` set opinion new-op`` update-color ;; 更新颜色映射`` ]``
`` set step-counter step-counter + 1`` tick``End`
你可以试着调整模型里的参数,比如不同个性观点的权重(self-weight)、群体规模大小(num-agents)等,看看这些因素会对观点演化的特点和速度产生怎样的影响。
观察模拟过程会发现,虽然已经实现了观点演化的过程,但好像没办法让整个群体快速达成观点统一。目前的群体观点分裂成几个“阵营”,形成了小范围的观点同化现象。
**
**
基本模型
**
**
2.2 实现主体的空间移动:改变主体社交范围
思考原因,很可能是因为社交关系固定不变,才导致形成了多个观点团体。如果想要实现整个群体的观点统一,是不是可以试试让成员的社交圈“流动”起来,在更大的范围内互相交换想法呢?
**
**
我们可以把这个思路抽象成具体规则,并用代码实现:在程序的运行模块里,给turtles(角色主体)增加移动的属性设置。 * *
fd 1 ;; 向前移动1单位距离`rt random 360 ;; 随机转向 `
我们可以发现,通过这个简单的改动,群体逐渐形成了统一的观点!
改变主体的社交范围
2.3 调整主体的态度属性:实现群体观点倾向性
在刚刚的代码里,我们把群体成员的观点设置成了从0到1的均匀分布。但在现实生活中,群体对特定事件的观点通常会有一定的倾向性。接下来,我们可以继续调试代码,通过设置群体观点的偏态分布规则,来模拟这种现象。
添加观点偏态分布模块: * * * * * *
to-report biased-random` let x random-normal 0.25 0.2`` if x < 0 [ set x 0 ]`` if x > 1 [ set x 1 ]`` report x``End`
这段代码采用的实现方式是,让观点均值为0.25,标准差设为0.2,这样能呈现出偏向消极且带有一定浮动空间的分布,同时还能保证所有样本都处于0到1的范围内。不过,实现这一目标并非只有这一种途径,你还可以尝试其它方法。
然后,在setup中调用该模块: *
set opinion biased-random
此时,群体观点的倾向性很明显。但是,在主体社交范围固定时,仍然有机会出现持有积极观点的小型团体。
**
**
观点偏态分布 固定社交范围 当个体逐渐改变社交范围时,群体观点同样逐渐同化,相较于观点均匀分布时的群体观点稳态,更加偏向消极。
同时,我们还可以发现,在同一套参数设置下进行多次实验,群体观点总能演化至同一水平。这表明,模型对舆论观点状态可以进行稳定预测。
**
**
观点偏态分布 主体流动交互
2.4 添加主体异质性:体现不同主体的独立思考能力差异
在上述模型中,假设所有主体都拥有相同的个性决策权重。但在现实生活中,不同个体的独立思考能力往往具有差异。我们可以添加主体异质性规则模拟这一现象,这也是 NetLogo 非常擅长的工作。
下面我们来添加一个生成异质性个性决策权重的函数: * * * * * *
to-report generate-self-weight` let w random-normal 0.5 0.2`` if w < 0.1 [ set w 0.1 ]`` if w > 0.9 [ set w 0.9 ]`` report w``end`
这段代码通过正态分布来生成处于0.1-0.9范围的个体观点权重,这里设定均值为0.5,标准差为0.2,如此一来,就能保证每个主体的独立思考能力具有差异。
同样,在setup中完成初始化即可: *
set self-weight generate-self-weight
请你在不同模型情境和参数设置下观察异质性主体的表现,看看可以得到什么启示?
现在,你已经明白了如何从生活中常见的场景入手,将这些现实问题转化为建模规则。接下来,你可以独立尝试自己感兴趣的话题,并通过数据输出结果或可视化图表来观察参数调整的效果。
3. 构造人工社会的核心思维
阿希实验与米尔格拉姆实验揭示了群体压力扭曲个体理性的惊人表现。但不容忽视的是,社会交互又是维系社会协作的神经中枢,涌现出超越个体认知的宏观秩序,驱动群体智慧演化。
以观点动力学建模为范例,我们能够洞悉构造人工社会的核心思维——主体属性、交互规则与社会环境,实现从现实问题到模型规则的转化。
或许你已萌生运用ABM方法探索科学问题的热忱。在此,**笔者有几点建议,帮助你明晰该方法的适用性。**首先,需判断待研究的科学问题是否属于“交互驱动型”。从研究方法论而言,理解交互规则是构建复杂适应性系统的逻辑起点,也是开展相关研究的必要前提。其次,复杂秩序往往源自简单主体的自适应交互过程,这要求研究者有针对性地建构主体属性与社会环境,建立恰当的抽象规则体系。并非所有社会现象都需引入主体异质性假设,“全知全能”的个体属性也并非人工社会模型追求的目标。另外,建模逻辑不是追求对系统的“全局操控”或细节设计,而是通过规则设计激发系统的自组织演化能力。
尽管当前Python库已支持调用包括观点动力学模型在内的多种建模工具,但我们仍需要通过自主编码实践,深度理解复杂适应系统建模的核心逻辑。通过掌握建模思维,你可以用代码自由验证脑海中灵光乍现的猜想,将探索的触角延伸至现实社会难以触及的梦幻,探索无限的可能性。那些挣脱常规范式的独立思辨,正是激发群体智慧涌现的密钥。
**
**
参考文献
[1] Bonabeau E. Agent-based modeling: Methods and techniques for simulating human systems [J]. Proceedings of the National Academy of Sciences, 2002, 99(suppl_3): 7280-7287. [2] Wen T, Zheng R, Wu T, et al. Formulating opinion dynamics from belief formation, diffusion and updating in social network group decision-making: Towards developing a holistic framework [J]. European Journal of Operational Research, 2025, 325(3): 381-399. [3] Shen Y, Ma X, Deveci M, et al. A hybrid opinion dynamics model with leaders and followers fusing dynamic social networks in large-scale group decision-making [J]. Information Fusion, 2025, 116: 102799. [4] Xu Y, Liu S, Cheng T C E, et al. Opinion convergence and management: Opinion dynamics in interactive group decision-making [J]. European Journal of Operational Research, 2025, 323(3): 938-951. [5] Yang Y, Li H, Gao S, et al. Interdependent evolutionary dynamics of opinion and strategy on two-layer networks [J]. Chaos, Solitons & Fractals, 2025, 191: 115933. [6] Ding G, Liu Z, Li S, et al. Impact of mindset types and social community compositions on opinion dynamics: A large language model-based multi-agent simulation study [J]. Computers in Human Behavior, 2025, 172: 108730. [7] Wang Y, Li X, Cheng Y, et al. A neural probabilistic bounded confidence model for opinion dynamics on social networks [J]. Expert Systems with Applications, 2024, 247: 123315.