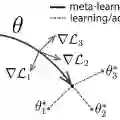
Despite recent advances in its theoretical understanding, there still remains a significant gap in the ability of existing PAC-Bayesian theories on meta-learning to explain performance improvements in the few-shot learning setting, where the number of training examples in the target tasks is severely limited. This gap originates from an assumption in the existing theories which supposes that the number of training examples in the observed tasks and the number of training examples in the target tasks follow the same distribution, an assumption that rarely holds in practice. By relaxing this assumption, we develop two PAC-Bayesian bounds tailored for the few-shot learning setting and show that two existing meta-learning algorithms (MAML and Reptile) can be derived from our bounds, thereby bridging the gap between practice and PAC-Bayesian theories. Furthermore, we derive a new computationally-efficient PACMAML algorithm, and show it outperforms existing meta-learning algorithms on several few-shot benchmark datasets.
翻译:尽管在理论理解方面最近有所进展,但现有PAC-Bayesian理论在元学习能力方面仍然存在巨大差距,无法解释在少数学习环境中改进业绩的情况,因为目标任务的培训实例数量极为有限,这一差距源于现有理论的假设,即所观察到的任务的培训实例数量和目标任务的培训实例数量都遵循同样的分布,而这种假设在实践中很少得到坚持。我们通过放松这一假设,发展了两个专门为少见学习设置定制的PAC-Bayesian界限,并表明两种现有的元学习算法(MAML和Reptile)可以来自我们的界限,从而缩小实践与PAC-Bayesian理论之间的差距。此外,我们从新的计算高效的PACMAML算法中推导出一个新的计算高效的PACMAML算法,并显示它优于几个点基准数据集的现有元学习算法。