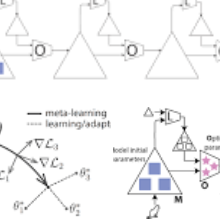
Multi-task learning (MTL) aims to improve the generalization of several related tasks by learning them jointly. As a comparison, in addition to the joint training scheme, modern meta-learning allows unseen tasks with limited labels during the test phase, in the hope of fast adaptation over them. Despite the subtle difference between MTL and meta-learning in the problem formulation, both learning paradigms share the same insight that the shared structure between existing training tasks could lead to better generalization and adaptation. In this paper, we take one important step further to understand the close connection between these two learning paradigms, through both theoretical analysis and empirical investigation. Theoretically, we first demonstrate that MTL shares the same optimization formulation with a class of gradient-based meta-learning (GBML) algorithms. We then prove that for over-parameterized neural networks with sufficient depth, the learned predictive functions of MTL and GBML are close. In particular, this result implies that the predictions given by these two models are similar over the same unseen task. Empirically, we corroborate our theoretical findings by showing that, with proper implementation, MTL is competitive against state-of-the-art GBML algorithms on a set of few-shot image classification benchmarks. Since existing GBML algorithms often involve costly second-order bi-level optimization, our first-order MTL method is an order of magnitude faster on large-scale datasets such as mini-ImageNet. We believe this work could help bridge the gap between these two learning paradigms, and provide a computationally efficient alternative to GBML that also supports fast task adaptation.
翻译:多任务学习(MTL)的目的是通过共同学习来改进若干相关任务的一般化。作为比较,除了联合培训计划外,现代元学习还允许在测试阶段使用带有有限标签的无形任务,希望能够迅速适应这些任务。尽管在问题形成过程中,MTL和元学习之间有着微妙的差别,但两种学习模式都有着相同的洞察力,即现有培训任务之间的共同结构可以导致更好的概括化和适应。在本文件中,我们迈出了重要的一步,通过理论分析和实证调查,理解这两个学习模式之间的密切关系。理论上,我们首先证明MTL与基于梯级的元学习(GBML)算法有相同的优化配置。我们随后证明,对于过于量化的神经网络来说,MTL和GBML的预测性功能是接近的。 特别是,这两个模型给出的预测力与相同的秘密任务相似。我们通过证明我们的理论结论是,在正确的执行中,MTL值与基于高等级的高级GL的高级算法中,这种高等级的高级的GMBML的计算方法往往具有竞争性的G-级的GMBML任务基准。