Optimisation of seismic imaging via bilevel learning

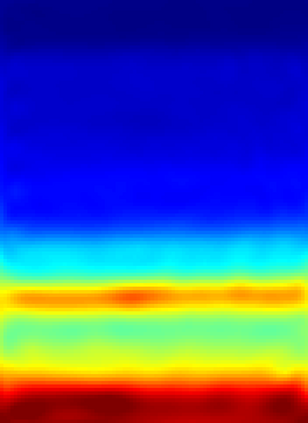
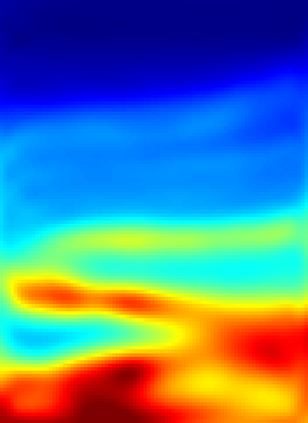
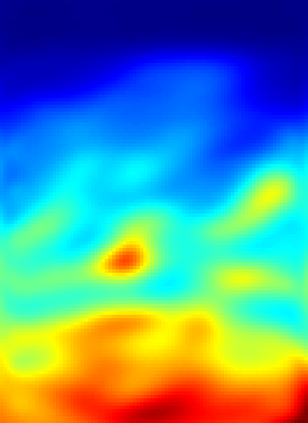
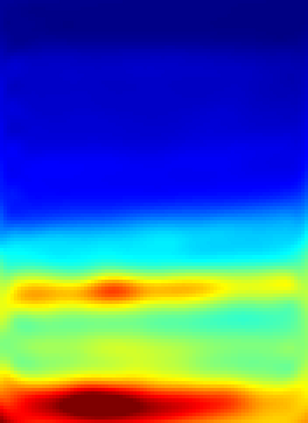
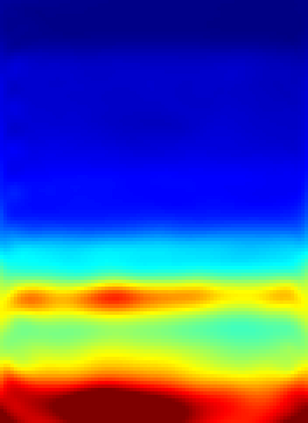
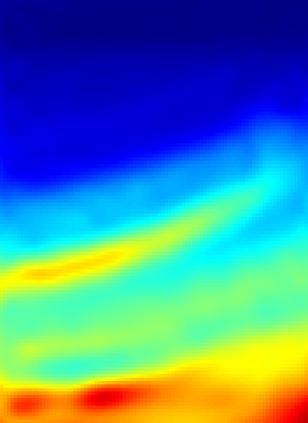
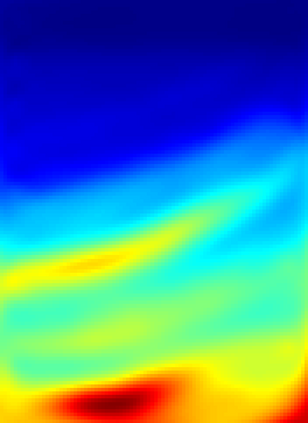
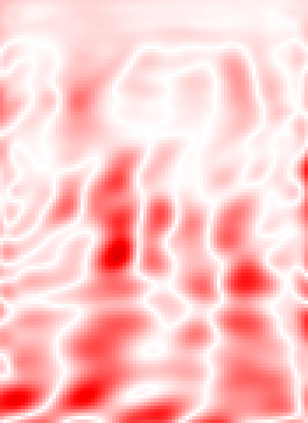
The implementation of Full Waveform Inversion (FWI) requires the a priori choice of a number of "design parameters", such as the positions of sensors for the actual measurements and one (or more) regularisation weights. In this paper we describe a novel algorithm for determining these design parameters automatically from a set of training images, using a (supervised) bilevel learning approach. In our algorithm, the upper level objective function measures the quality of the reconstructions of the training images, where the reconstructions are obtained by solving the lower level optimisation problem - in this case FWI. Our algorithm employs (variants of) the BFGS quasi-Newton method to perform the optimisation at each level, and thus requires the repeated solution of the forward problem - here taken to be the Helmholtz equation. The paper focuses on the implementation of the algorithm. The novel contributions are: (i) an adjoint-state method for the efficient computation of the upper-level gradient; (ii) a complexity analysis for the bilevel algorithm, which counts the number of Helmholtz solves needed and shows this number is independent of the number of design parameters optimised; (iii) a bilevel frequency-continuation strategy that helps avoiding convergence to a spurious stationary point; (iv) an effective preconditioning strategy for iteratively solving the linear systems required at each step of the bilevel algorithm; (v) a smoothed extraction process for point values of the discretised wavefield, necessary for ensuring a smooth upper level objective function. The advantage of our algorithm is demonstrated on a problem derived from the standard Marmousi test problem.