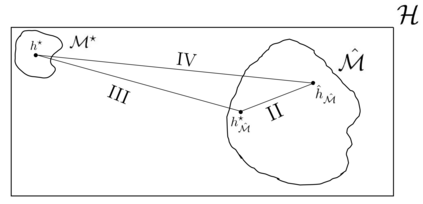
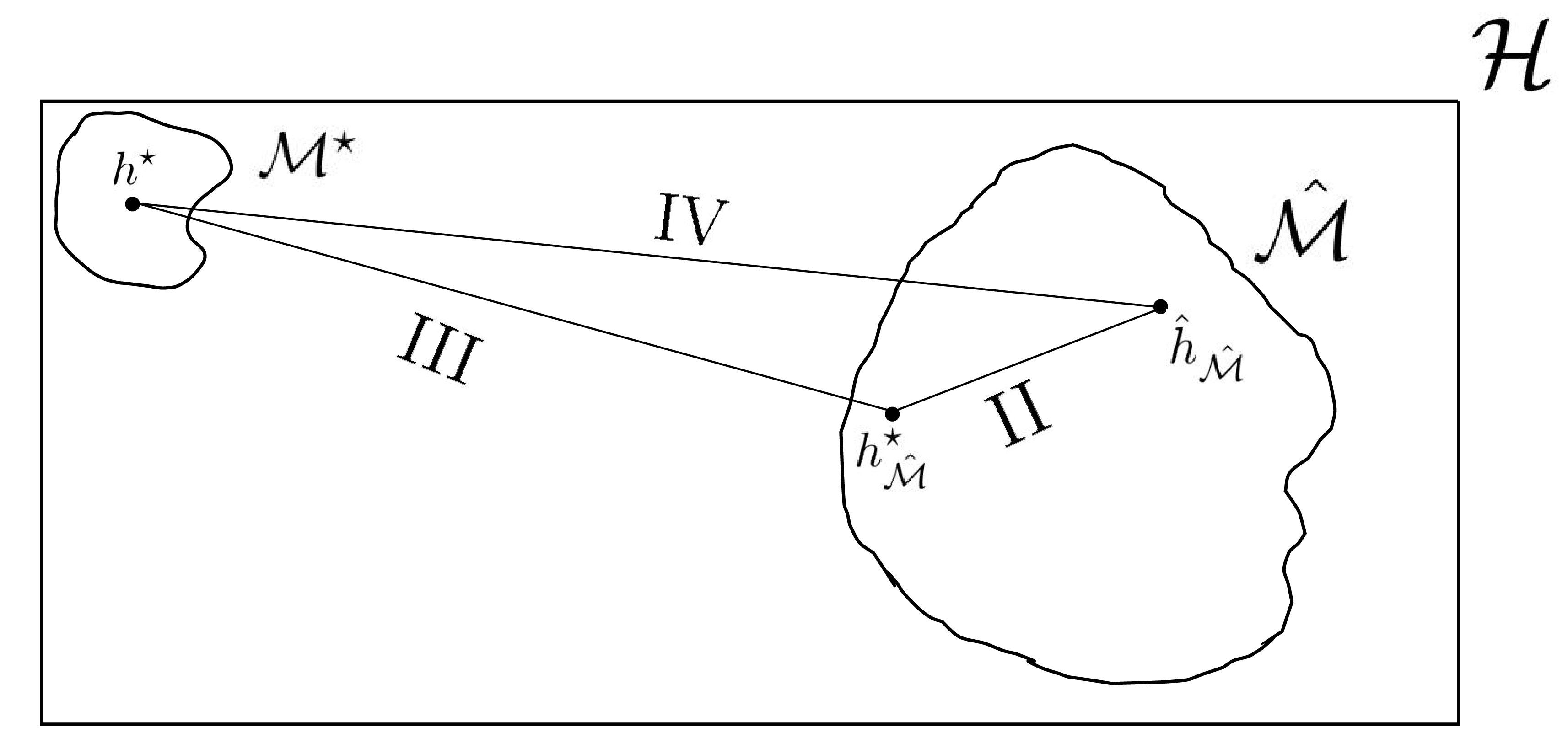
Cross-validation techniques for risk estimation and model selection are widely used in statistics and machine learning. However, the understanding of the theoretical properties of learning via model selection with cross-validation risk estimation is quite low in face of its widespread use. In this context, this paper presents learning via model selection with cross-validation risk estimation as a general systematic learning framework within classical statistical learning theory and establishes distribution-free deviation bounds in terms of VC dimension, giving detailed proofs of the results and considering both bounded and unbounded loss functions. We also deduce conditions under which the deviation bounds of learning via model selection are tighter than that of learning via empirical risk minimization in the whole hypotheses space, supporting the better performance of model selection frameworks observed empirically in some instances.
翻译:在统计和机器学习中广泛使用风险估计和模型选择的交叉验证技术,但是,对通过模型选择和交叉验证风险估计进行学习的理论特性的了解程度很低,因为其广泛使用。在这方面,本文件介绍了通过模型选择和交叉验证风险估计进行学习的情况,作为传统统计学习理论中的一般系统学习框架,并按VC层面确定了无分配偏差的界限,详细证明了结果,并考虑了受约束和无限制的损失功能。我们还推断出,通过模型选择进行学习的偏差比通过在整个假设空间最大限度地减少经验风险来学习的偏差范围更为紧密,支持在某些情况下更好地执行经验观察的模型选择框架。</s>