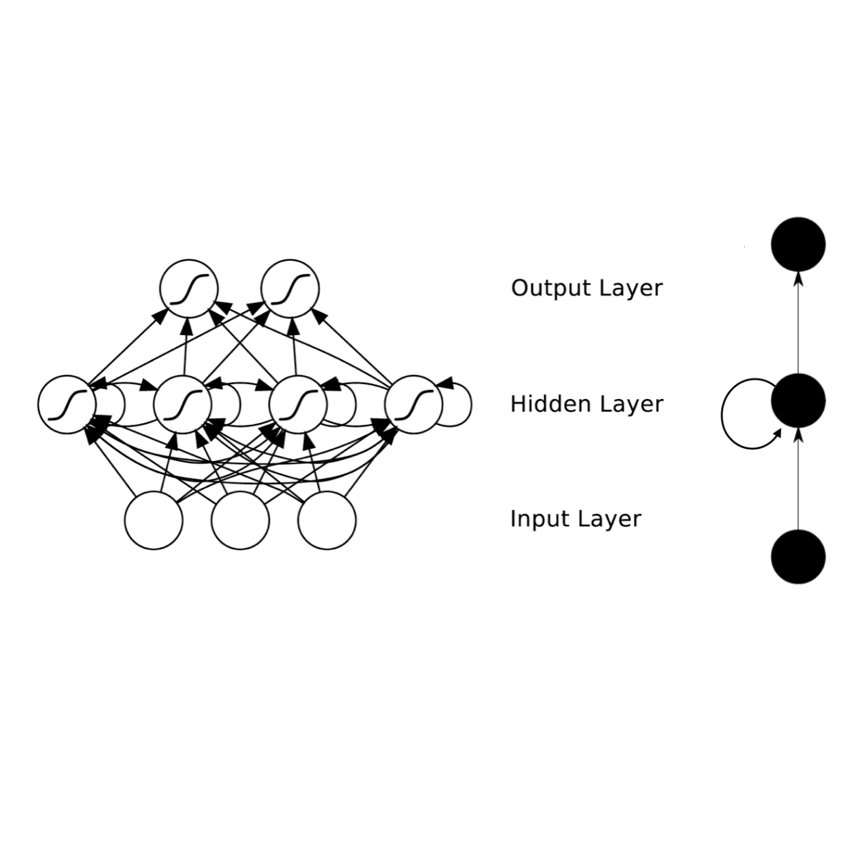
Meta-learning of numerical algorithms for a given task consist of the data-driven identification and adaptation of an algorithmic structure and the associated hyperparameters. To limit the complexity of the meta-learning problem, neural architectures with a certain inductive bias towards favorable algorithmic structures can, and should, be used. We generalize our previously introduced Runge-Kutta neural network to a recursively recurrent neural network (R2N2) superstructure for the design of customized iterative algorithms. In contrast to off-the-shelf deep learning approaches, it features a distinct division into modules for generation of information and for the subsequent assembly of this information towards a solution. Local information in the form of a subspace is generated by subordinate, inner, iterations of recurrent function evaluations starting at the current outer iterate. The update to the next outer iterate is computed as a linear combination of these evaluations, reducing the residual in this space, and constitutes the output of the network. We demonstrate that regular training of the weight parameters inside the proposed superstructure on input/output data of various computational problem classes yields iterations similar to Krylov solvers for linear equation systems, Newton-Krylov solvers for nonlinear equation systems, and Runge-Kutta integrators for ordinary differential equations. Due to its modularity, the superstructure can be readily extended with functionalities needed to represent more general classes of iterative algorithms traditionally based on Taylor series expansions.
翻译:用于特定任务的数字算法的元化学习包括由数据驱动的对算法结构及相关超参数的识别和调整。为了限制元学习问题的复杂性,可以而且应该使用对有利的算法结构有某种感性偏向的神经结构。我们把以前引入的龙格-库塔神经网络推广到一个循环的经常性神经网络(R2N2),用于设计定制的迭代算法的超级结构。与现成的深层次学习方法相反,它为生成信息并随后将这一信息组合成解决方案的模块设置了一个不同的分工。一个子空间的本地信息形式由从目前的外部外向下、内、反复函数评价产生。对下一个外向外的更新是这些评价的线性组合,减少这一空间的剩余部分,构成网络的输出。我们证明,在各种计算问题分类的输入/输出序列中,对于各种输入/输出序列的快速度参数,以子空间结构的形式生成类似常规的反复函数评价, Klovelutal-listria 等式的直径解式等式系统,对于Kloovtarial-listralli-listrallistrylistry listrue-listallistallistallistallistallistallistallical 等式的系统来说,对Kcallicallistallicallical-licallicallical 等式等等等式的系统进行类似。