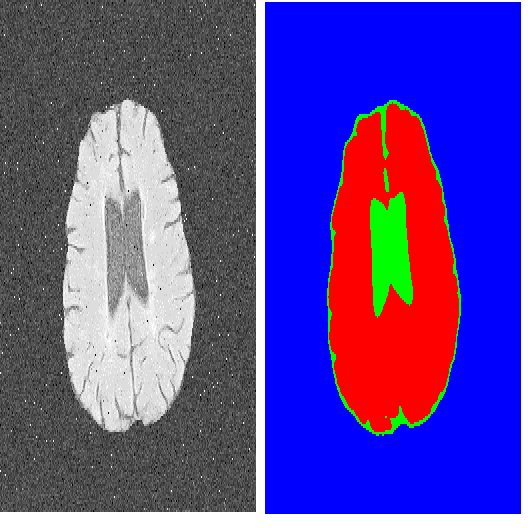
Random field and random cluster theory are used to prove certain mathematical results concerning the probability distribution of image pixel intensities characterized as generic $2D$ integer arrays. The size of the smallest bounded region within an image is estimated for segmenting an image, from which, the equilibrium distribution of intensities can be recovered. From the estimated bounded regions, properties of the sub-optimal and equilibrium distributions of intensities are derived, which leads to an image compression methodology whereby only slightly more than half of all pixels are required for a worst-case reconstruction of the original image. An example in unsupervised object detection illustrates the mathematical results.
翻译:随机字段和随机群集理论被用于证明某些关于图像像素强度概率分布的数学结果,这些像素强度被定性为通用 $2D$整数数阵列。图像中最小的边缘区域的大小被估计用于分割图像,从中可以回收强度的均衡分布。从估计的封闭区域中可以得出强度的亚优度和均衡分布的属性,这导致一种图像压缩方法,即只有略多于所有像素的一半用于原始图像最坏情况下的重建。一个未经监督的天体探测的示例显示了数学结果。