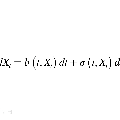带跳随机时滞微分方程解的高效快速算法设计及其在美式未定权益定价中的应用

项目名称： 带跳随机时滞微分方程解的高效快速算法设计及其在美式未定权益定价中的应用

项目编号： No.11526193

项目类型： 专项基金项目

立项/批准年度： 2016

项目学科： 数理科学和化学

项目作者： 周艳丽

作者单位： 中南财经政法大学

项目金额： 3万元

中文摘要： 在金融保险领域，很多随机问题需要考虑时间延迟(时滞)和重大事件(跳现象)的影响。因此，对带跳随机延迟微分方程的研究将有助于对金融保险现象进行更精确的描述。由于这类方程的解析解很难得到，所以设计有效的数值逼近方法并分析其数值解的收敛性和稳定性具有重要的理论意义和实际应用价值。本项目基于一般随机微分方程弱解的数值算法理论，拟针对levy过程驱动下的随机时滞微分方程，设计高效快速算法对其弱解进行数值逼近，并证明这种新算法的收敛阶和均方稳定性。然后，在带跳且具时滞的金融市场条件下，通过levy过程驱动下的随机时滞微分方程的数值弱解给出美式未定权益的合理定价。

中文关键词： 随机微分方程；美式期权定价；参数校准；动态套期保值；实物期权

英文摘要： In the area of finance and insurance, many stochastic problems are affected by time-delay and significant events. Thus, the study of stochastic delay differential equations with jumps is very important to capture the essence of these problems. Since they hardly admit analytical solutions, it is critical to develop efficient discrete-time approximation methods and study their numerical properties of convergence and stability. Based on the exisiting theory of numerical solutions of stochastic differential equation, this project aims to design a new efficient and fast simulation algorithm for the stochastic delay differential equation driven by Levy process and then study its convergence rate and mean-square stability. Moreover, in the financial market with time lag and jumps, the price of the American contingent claims will be derived from the numerical weak solutions of stochastic delay differential equation driven by Levy process.

英文关键词： Stochastic differential equation；American option pricing；Parameter calibration；Dynamic hedging；Real option