【AAAI 2022】神经分段常时滞微分方程

神经分段常时滞微分方程

Neural Piecewise-Constant Delay Differential Equations 

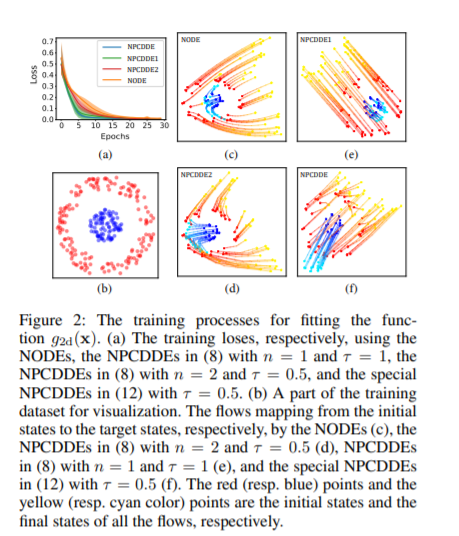
论文摘要：神经微分方程作为标准的连续深度神经网络框架，在时间序列分析，生成模型构建，物理系统建模等领域取得了广泛应用。但神经微分方程的微分同胚性质导致其不具备万有逼近能力。为了克服该问题，不少学者提出了相应的连续深度神经网络框架，比如，增维神经常微分方程、神经时滞微分方程（neural delay differential equation, NDDEs）等。本文中, 我们提出一类新的具有时滞的连续深度神经网络，称为神经分段常时滞微分方程（neural piecewise-constant delay differential equations, NPCDDEs）。在这里, 与之前提出的 NDDEs 框架不同，我们将单个时滞转换为分段常时滞（piecewise-constant delay）。经过这样转换后的 NPCDDEs 一方面继承了 NDDEs 中的万有逼近能力的优势，另一方面，NPCDDEs 考虑了多个过去时刻的信息, 进一步提高了模型能力。通过这样的推广, 我们在 1 维分段常时滞种群动力学以及图像数据集 MNIST、CIFAR10和SVHN上，证明了 NPCDDEs 的卓越性能。

论文开创性突破与核心贡献：AAAI 论文评审人充分认可了本文提出的神经分段常时滞微分方程及相关理论分析，认为其实验结果令人信服。

https://www.zhuanzhi.ai/paper/c8575423064fbc7f25f3e9f32b26c170

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“NPCD” 就可以获取《【AAAI 2022】神经分段常时滞微分方程》专知下载链接

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，查看本篇文档专知下载