障碍和触碰期权的定价
2018 年 12 月 20 号在万矿全球量化嘉年华邀请做了一个“障碍和触碰期权定价”的演讲。进入王的机器公众号,回复 BTO 可下载完整 PPT
说实话,对于该 PPT 里面的内容,1 个小时是远远不够的。而且在线上讲演我也不能用手势或者鼠标来强调重点,因此我感觉到可能有些读者会听得云里雾里,所以在此帖我为大家写下了更多细节。希望有用。
整个讲演分四个部分:
概览 (为什么会使用障碍期权,为什么需要对其准确定价)
分类 (按照障碍个数、障碍方向、敲入敲出特征、看涨看跌类别、窗口类型)
定价模型和方法 (通用于所有衍生品,从简单到复杂的 BS, VV, LV, SV 和 SLV 模型)
偏微分方程有限差分和蒙特卡洛 (一维和二维、举例部分窗口期权定价)
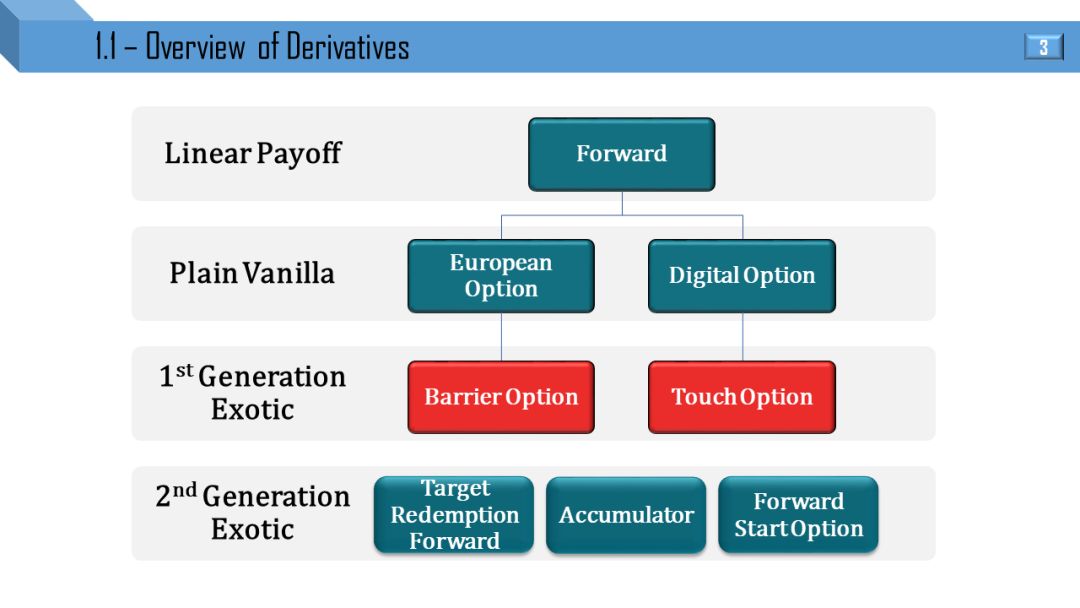
衍生品由易到难:
线性类型的远期 -->
简单的欧式和数字期权 -->
第一代奇异类的障碍和触碰期权 -->
第二代奇异类的目标赎回远期和累计期权
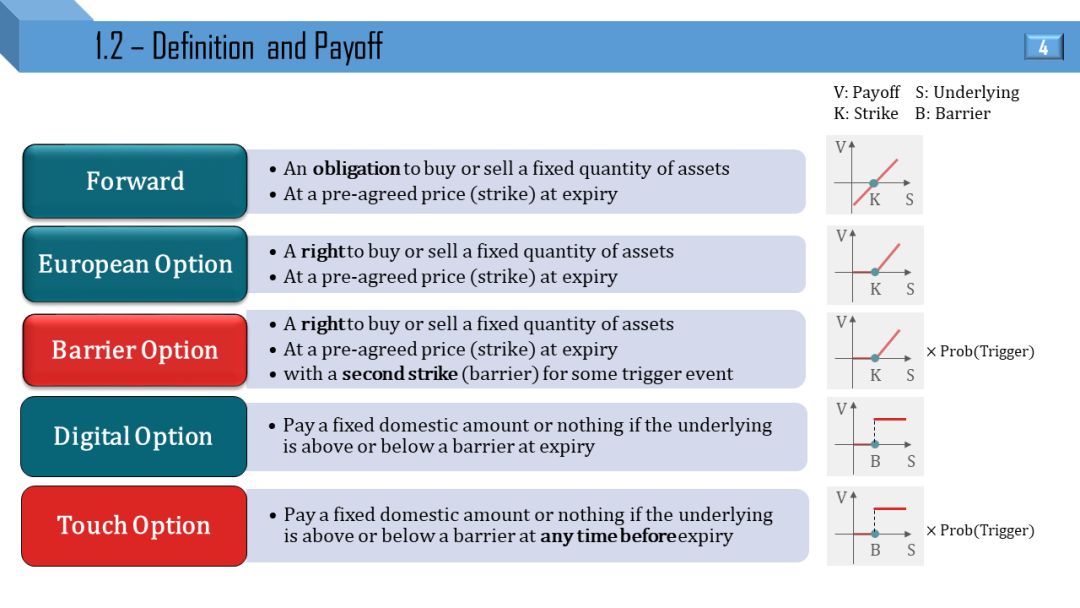
远期是承诺,期权是权利。障碍期权在欧式期权加上一些触发事件,触碰在数字期权加上一些触发事件。以多头远期 (long)、欧式看涨期权 (call),向上敲出障碍期权 (up-and-out call),数字看涨期权 (digital call),和向上触碰期权 (one touch up) 举例,它们的支付函数为 (T 是到期日,t 在 0 和 T 之间)
远期 = ST - K
欧式期权 = (ST - K)+
障碍期权 = (ST - K)+ · I{St < B}
数字期权 = I{ST > K}
触碰期权 = I{ST > K} · I{St < B}
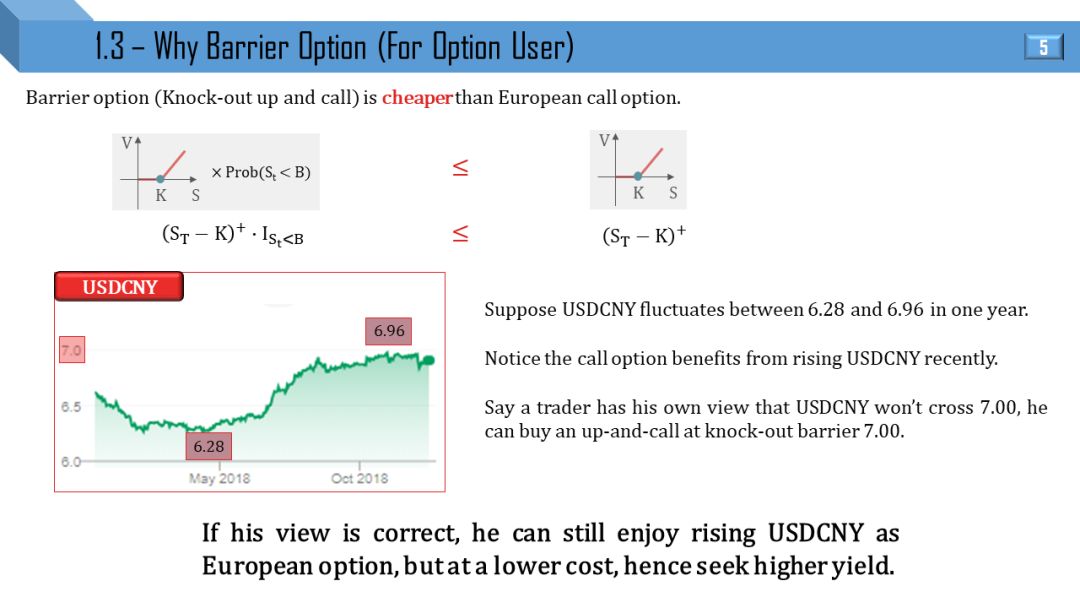
为什么买敲出或敲入障碍期权?比同等的欧式期权便宜!同等的意思是同样的行权价格、同方向的障碍水平、相等的到期日。前提是对市场的看法要准确 (见上图 USDCNY 的例子)。
为什么需要准确定价障碍期权?因为它们是更复杂产品或者交易策略 (strategy) 的基本组成部分。举例盒式远期 (box forward, BF),根据其支付函数可推出
BF = DOP - DOC + UOC - UOP
为了给准确这个策略定价,是不是需要准确定价其四个组成部分的障碍期权呢?
障碍期权最重要要点:
敲出 - 只要 S 碰到障碍,期权无效 (有时会给个返还);否则是欧式期权
敲入 - 如果 S 没碰到障碍,期权无效 (有时会给个返还);否则是欧式期权
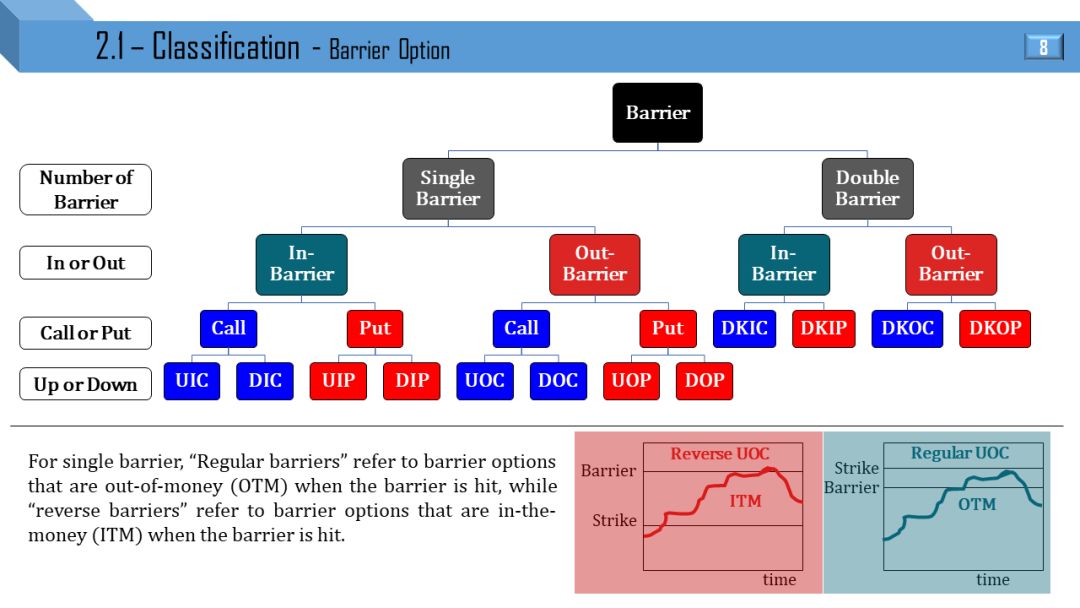
障碍期权分类如下:
第一层:单障碍、双障碍
-->
第二层:敲出和敲入
-->
第三层:看涨和看跌
--> (只适合单障碍)
第四层:上障碍、下障碍
--> (只适合单障碍)
第五层:普通类型、反向类型
普通类型 (regular barrier):
对于敲出期权,期权在触碰障碍时 OTM 不变
对于敲入期权,期权在触碰障碍时 ITM 不变
反向类型 (reverse barrier):
对于敲出期权,期权在触碰障碍时从 ITM 变成 OTM
对于敲入期权,期权在触碰障碍时从 OTM 变成 ITM
触碰期权最重要要点:
触碰 - 只要 S 碰到障碍,给个返还;否则期权无效
不触碰 - 如果 S 没碰到障碍,给个返还;否则期权无效
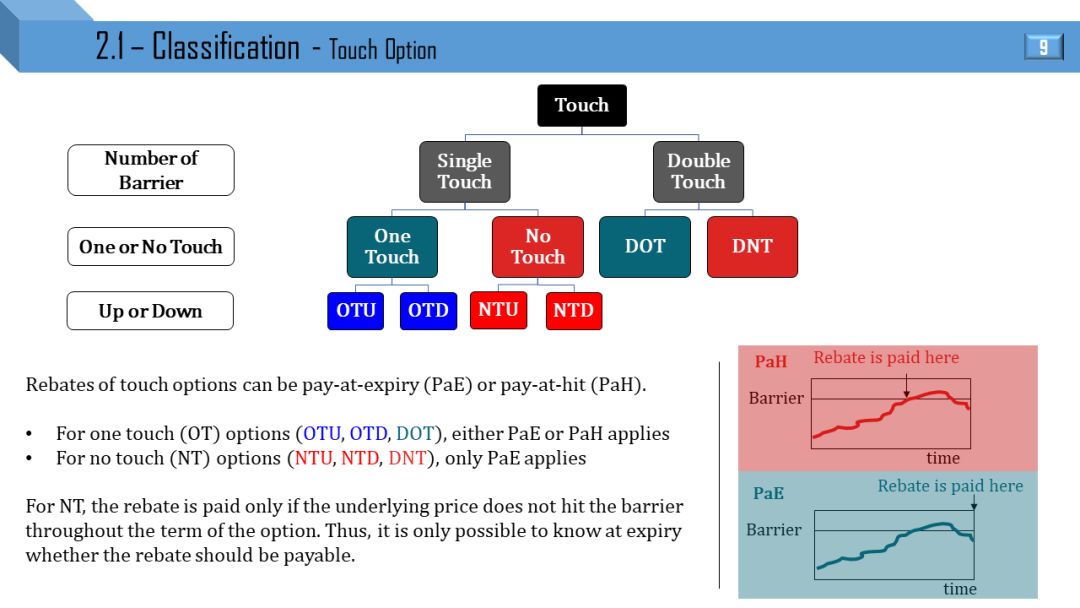
触碰期权分类如下:
第一层:单障碍、双障碍
-->
第二层:触碰和不触碰
--> (只适合单障碍)
第三层:上障碍、下障碍
触碰期权的返还支付方式也有两种:
触碰即支付 (pay-at-hit, PaH):OT 类
到期日支付 (pay-at-expiry, PaE):OT 类和 NT 类
NT 类返还只能 PaE,原因是不到到期日 (expiry),根本不能确定 S 是否没有碰到障碍,而 OT 类返还只要当 S 碰到障碍,就能确定下来时点,因此可以 PaH 和 PaE。
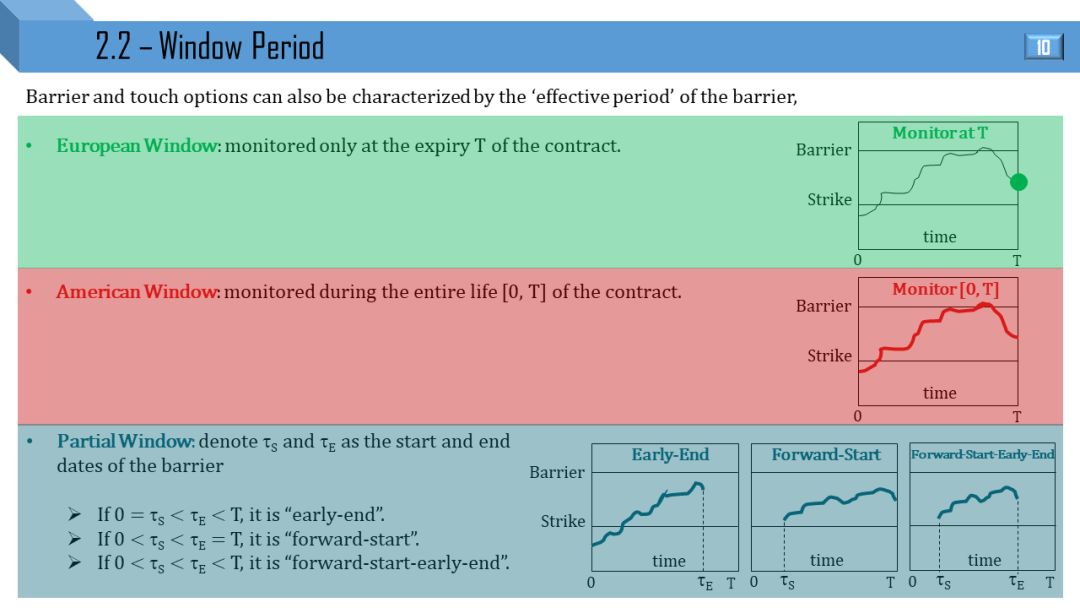
根据观测的障碍窗口,可分为
欧式窗:只在到期日 T 观测
美式窗:在 0 到 T 观测
部分窗:在 0 到 T 取一段观测,再细分为
远期开始 (forward start)
提前终止 (early end)
远期开始提前终止 (forward start early end)
平价公式 1:NT + OT = 折现返还
平价公式 2:KO + KI = 欧式
平价公式和模型无关,和障碍数目无关,和障碍水平的方位无关、和障碍的窗口无关。根据经验 OT 和 KO 比较容易定价,由两个平价公式可以很快计算出相对应的 NT 和 KI 价格。那么计算 OT 和 KO 需要什么样的定价模型 (pricing model) 和定价方法 (pricing method) 呢?
3.1
金融产品估值
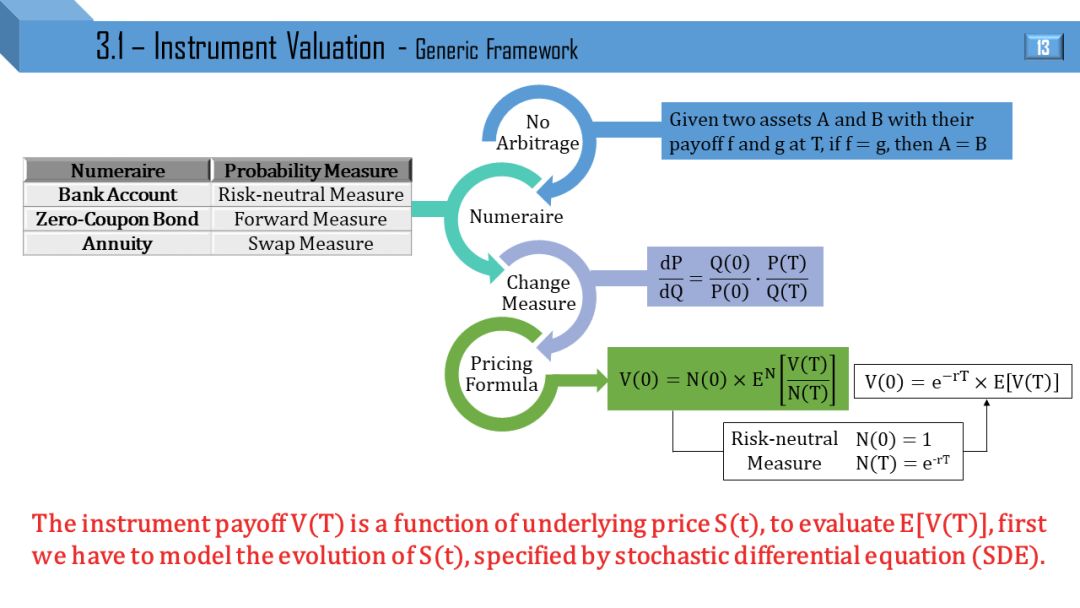
通用方法是运用无套利原则,选择等价计量物,必要时候改变测度,可推出定价公式。简单说就是计算 E[V(T)],即 V(T) 的期望值。又因为支付函数 V(T) 是 S(t) 的函数,因此需要对 S(t) 建模,即写出 S(t) 的随机微分方程 (SDE)。
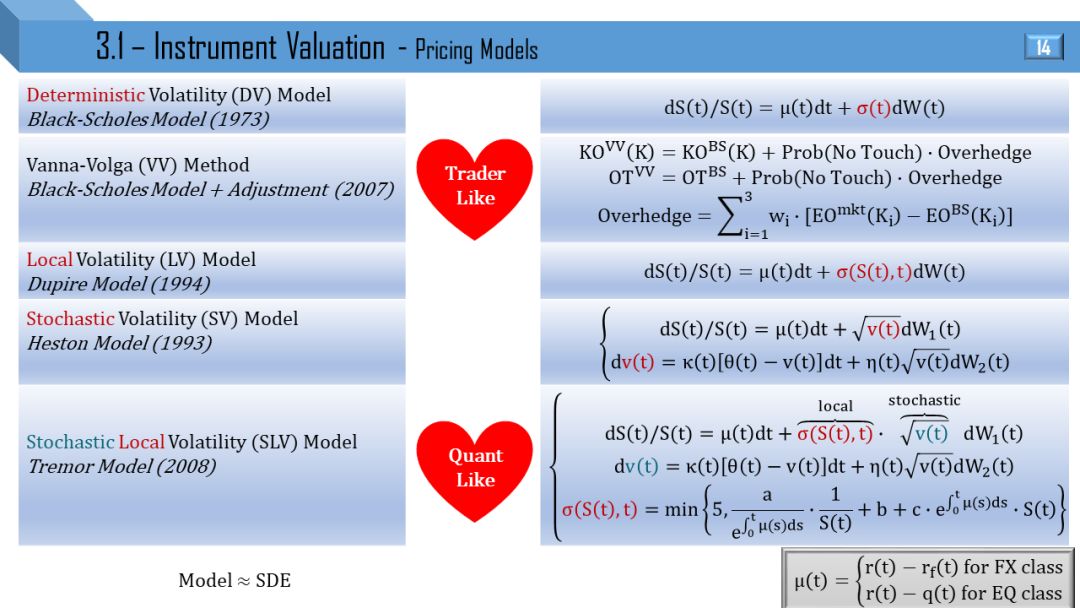
定价模型从上到下由易到难:
确定波动率 (DV, Black-Scholes)
-->
对冲掉波动率风险 (VV)
-->
局部波动率 (LV, Dupire)
-->
随机波动率 (SV, Heston)
-->
随机局部波动率 (SLV, Tremor)
BS, VV 和 LV 都是一维模型,只对原生资产价格建模;而 SV 和 SLV 是二维模型,对原生资产价格和波动率建模。
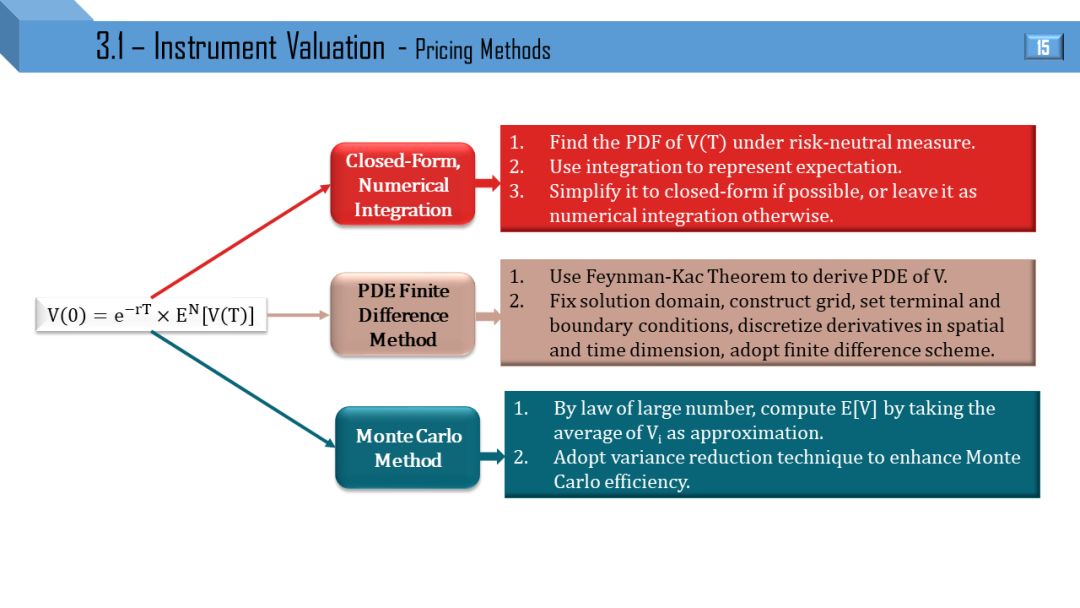
计算期望值 E[V(T)] 有三种方法:
硬推公式,把 E[] 用积分表示,能推出来就是解析解 (closed-form),不能退出来就留着积分,叫半解析解 (semi-closed form)。
用 Feyman-Kac 定理,将 V(0) = E[] 的偏微分方程 (Paritial Differential Equation, PDE) 形式写出来,用有限差分 (finite difference, FD) 数值解。
用采样 (sampling) 和模拟 (simulation) 的模特卡洛 (Monte Carlo, MC) 方法,将 E[] 用简单的算术平均表示出来,可以用不同的方差缩减法来减小采样误差。
3.2
解析解和半解析解
BS 模型下欧式期权的解析解,Heston 模型下欧式期权的半解析解 (主要到红色椭圆圈的数值积分项)。
3.3
偏微分方程有限差分法
Feynman-Kac 是联系 SDE 和 PDE 的纽带:
SDE 红色的漂移项 (drift) μ 变到了 PDE 的 ∂V/∂x 前面
SDE 蓝色的扩散项 (diffusion) σ 变到了 PDE 的 ∂2V/∂x2 前面
此外绿色的支付函数 h 就是 PDE 的终止条件。
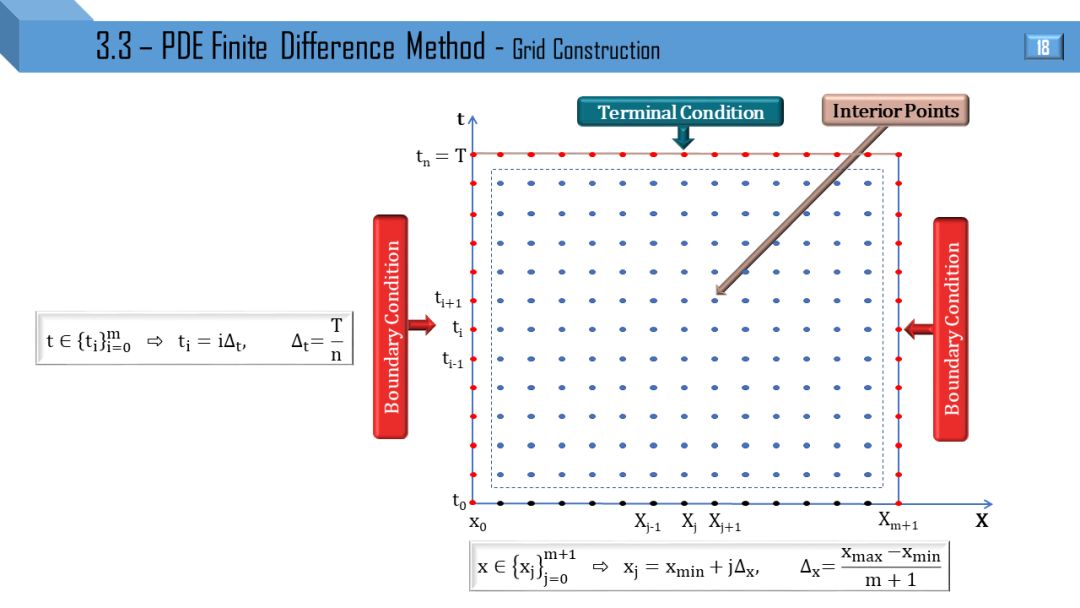
构建网格:
制定 t 维度下界为 0,上界为 T,其中 T 是金融产品的到期日,完全可以从其交易证实 (termsheet) 得到
制定 x 维度的下界,通常对于股价、汇率的下界就是 0 (或者下障碍),上界要通常等于 x(0) 和 K 的最大值乘以 4 (或者上障碍)。
制定终止条件,可从 termsheet 中得到金融产品的 payoff
制定边界条件,这个比较 tricky,是 PDE 里的难点
连续的 PDE 没办法解,只能里面的各个偏导数离散化,将 PDE 变成差分方程 (difference equation)。离散方式有三种:
完全显性 (fully explicit):加强版的三叉树,计算快但结果不是绝对稳定,通常不用
完全隐性 (fully implicit):计算结果绝对稳定,但结果线性收敛,通常从 T 点开始解时用
克兰克-尼科尔森 (Crank Nicolson):计算结果几乎绝对稳定,结果二阶收敛,通常被使用
在某个时间 t,每个点离散后都是一个方程,全部结合以来就是一组线性方程,可写成矩阵形式。解 PDE 就是制定好终止条件和边界条件好,从 T 到 0 向后一步步解上面的矩阵方程。
3.4
蒙特卡洛法
采样 (sampling) 和模拟 (simulation) 经常被混淆:
采样:给定一个时点,在空间维度 (spatial dimension) 生成一维随机变量
模拟:给定多个时点,即在时间维度 (temporal dimension) 也在空间维度上生成两维随机变量。
采样适用于欧式期权定价,模拟适用于美式和障碍期权定价。
大数定理:从总体中选出 n 个独立同分布 (i.i.d) 的随机变量,计算样本均值 (sample mean),当 n 越大时,样本均值越趋近总体均值 (population mean) μ。
中心极限定理:当一组 i.i.d 随机变量的总体均值和标准差为 μ 和 σ,那么
(样本均值 - μ) / s(n)/n1/2 服从标准正态分布
上式分母 s(n)/n1/2 称为标准误差 (standard error),也是采样误差 (sampling error)。减小它有两个方法:
增大样本数 n,但是 n 上面有个根号,效率不高
直接减小样本方差 σY
第二种方法可以理解是用更聪明的采样得到新的一组 Ynew,使得
方差(Ynew) < 方差(Y)
而确保均值不变
均值(Ynew) = 均值(Y)
样本 Ynew 或 Y 可想成期权的支付值,期权价格就是 Ynew 或 Y 的均值,如果用一组更聪明的采样使得方差减小但均值变了,那不是适得其反么?
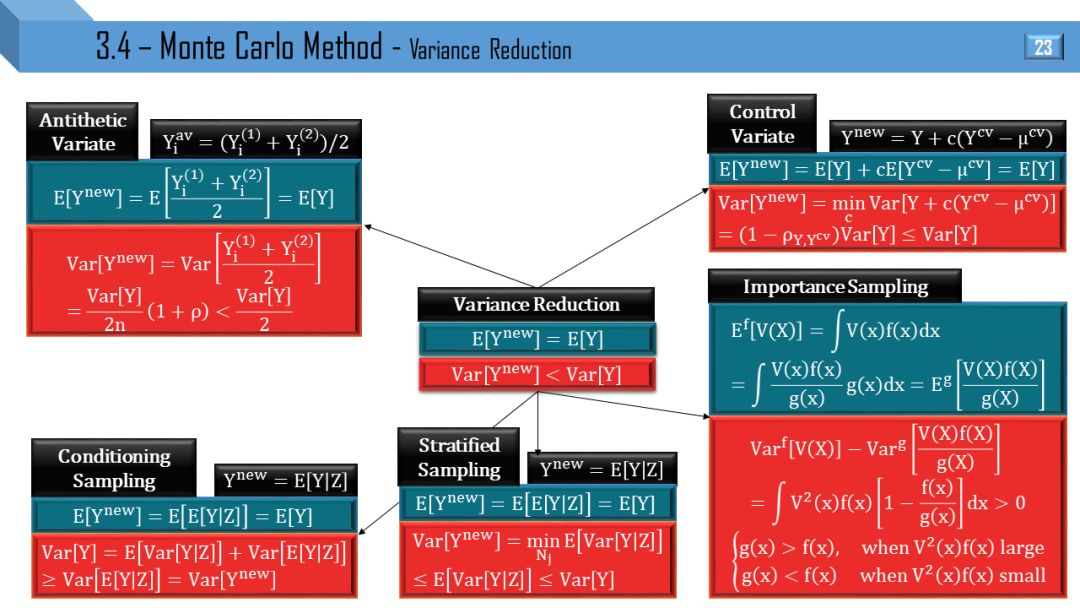
方差缩减核心就是用聪明的采样,减低方差,保住均值。方法有很多,由易到难,由无脑生成到精心设计:
对立变量 (Antithetic Variate):几乎什么时候都能用,万金油
控制变量 (Control Variate):知道随机变量 X 的期望,而 Y 和 X 正相关,比如用几何平均亚式期权当控制变量 X,来对算术平均亚式期权 Y的价格
条件抽样 (Conditioning Sampling):Var[Y] > Var[E[Y|Z]],假设 Y 是服从学生分布,那么 Y = X / Z1/2,其中 X 是正态分布而 Z 是卡方分布,那么给定一个特定 Z = z 值,Y 不就是正态分布了吗?因此 Z 从卡方分布用采样,Y|Z 就可以从正态分布中采样了。
分层抽样 (Stratified Sampling):Var[Y] > E[Var[Y|Z]],给定一个特征 Z = z 值后在 Y 上采样,叫做层 (strata)。
重要性抽样 (Importance Sampling):运用变换概率测度的方法,比如深度价外看涨期权 (K 远大于 S) 的模拟的很多路径都得到 0 的支付,这样模拟效果比较低,因此可能平移 S 的漂移项而改变 S 的分布。
条件抽样和分层抽样非常类似,它们的都是由 Law of total variance 推出来的
Var[Y] = Var[E[Y|Z]] + E[Var[Y|Z]]
上式右边两项都大于零,因此左项大于右边任意一项,有
Var[Y] > Var[E[Y|Z]] 是条件抽样,在 Z 上采样
Var[Y] > E[Var[Y|Z]] 是分层抽样,选择一个 z 值再在 Y 上采样
蒙特卡洛方法可以处理三种问题:
SDE 有解的,产品支付函数是欧式的:只用采样一个时点 (多条路径),只有采样误差,没有离散误差。
应用:BS 模型欧式期权
SDE 有解的,产品支付函数和路径有关:需要采样多个时点 (多条路径),只有采样误差,没有离散误差。
应用:BS 模型美式、障碍期权
SDE 没有解:需要采样多个时点 (多条路径),即有采样误差,又有离散误差。
应用:Heston 模型欧式,美式、障碍期权
4.1
一维模型 - 偏微分方程差分
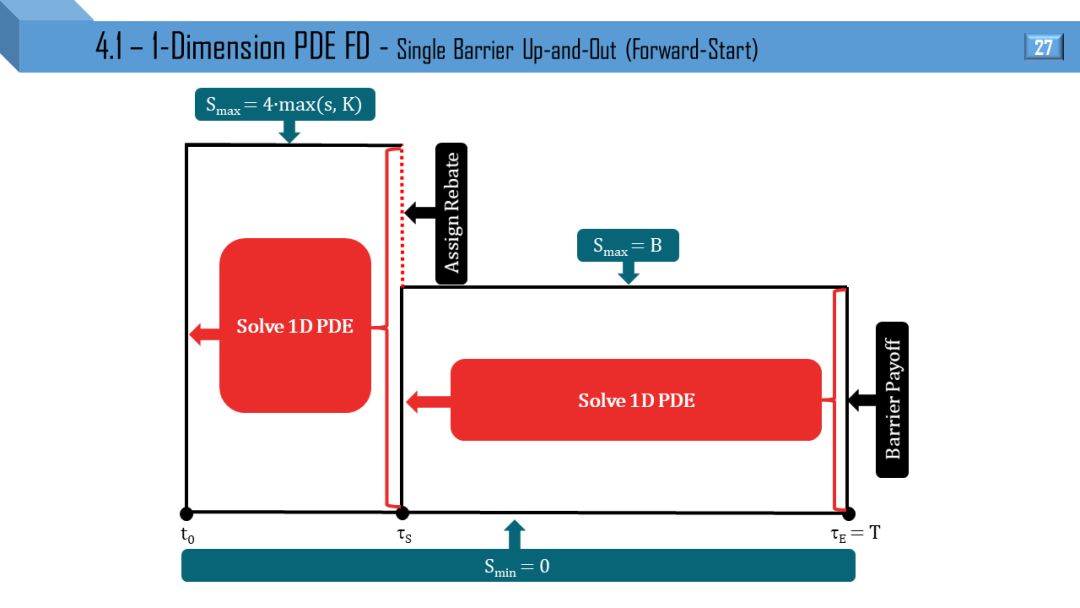
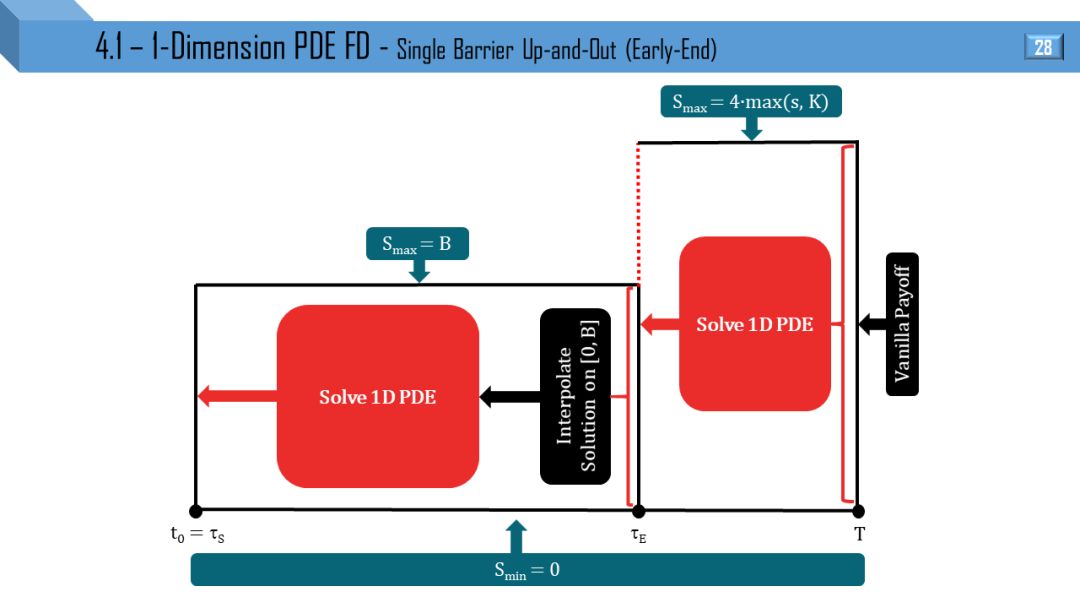
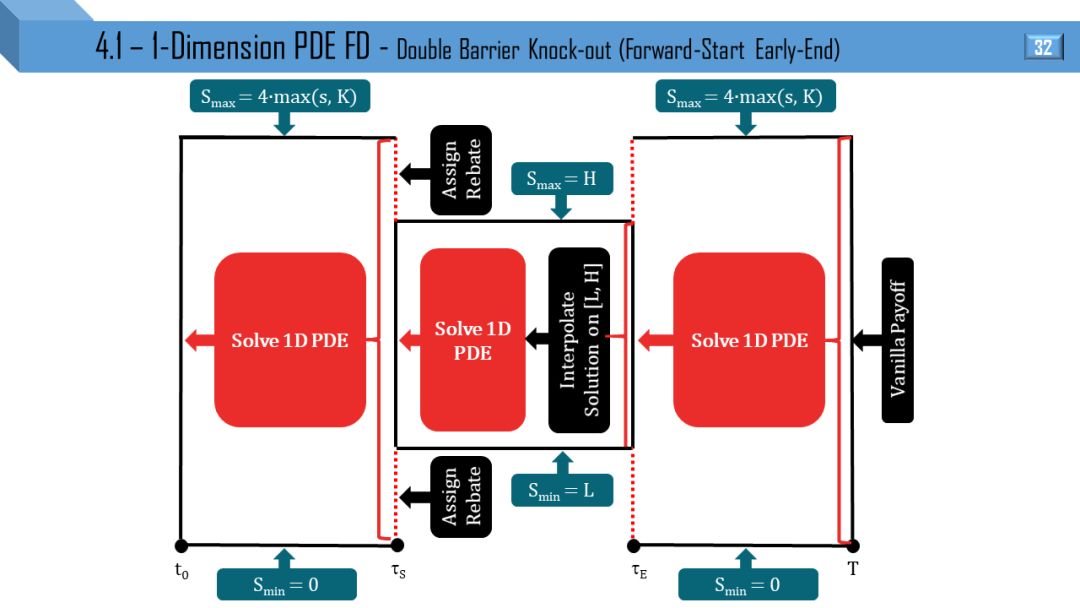
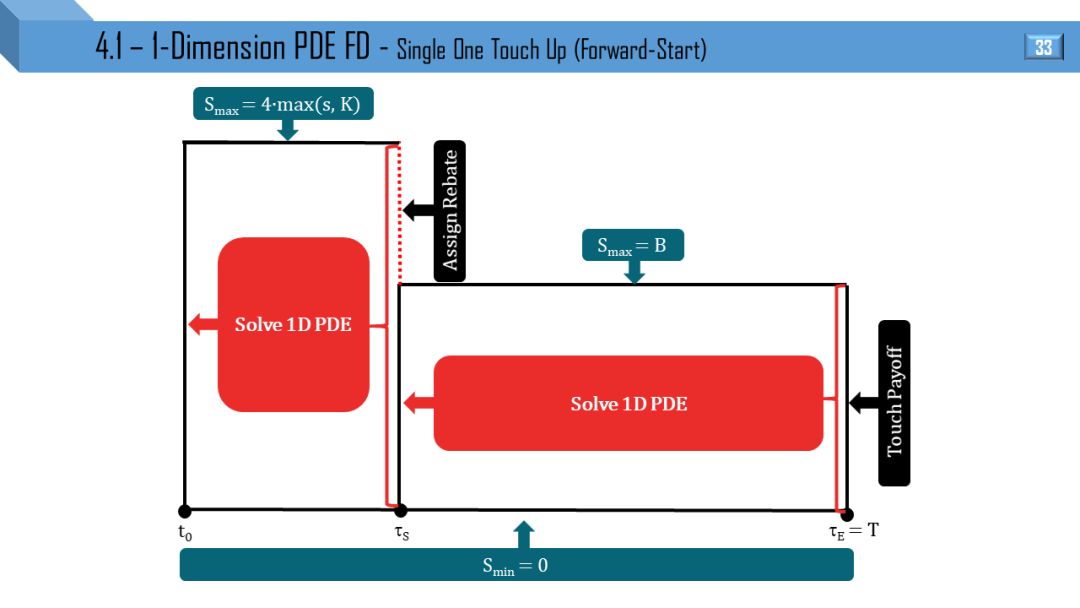
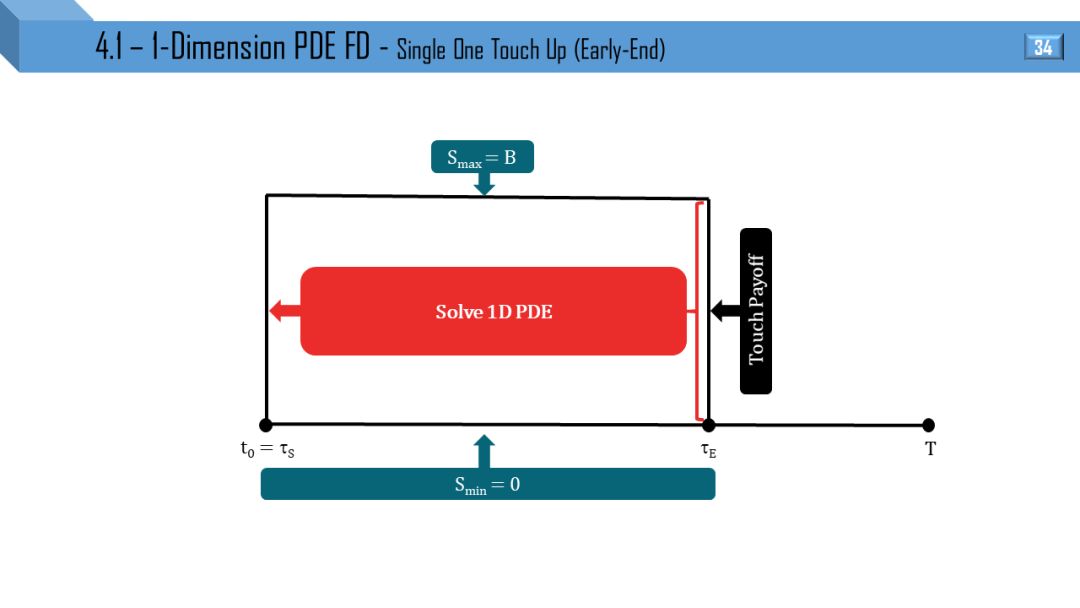
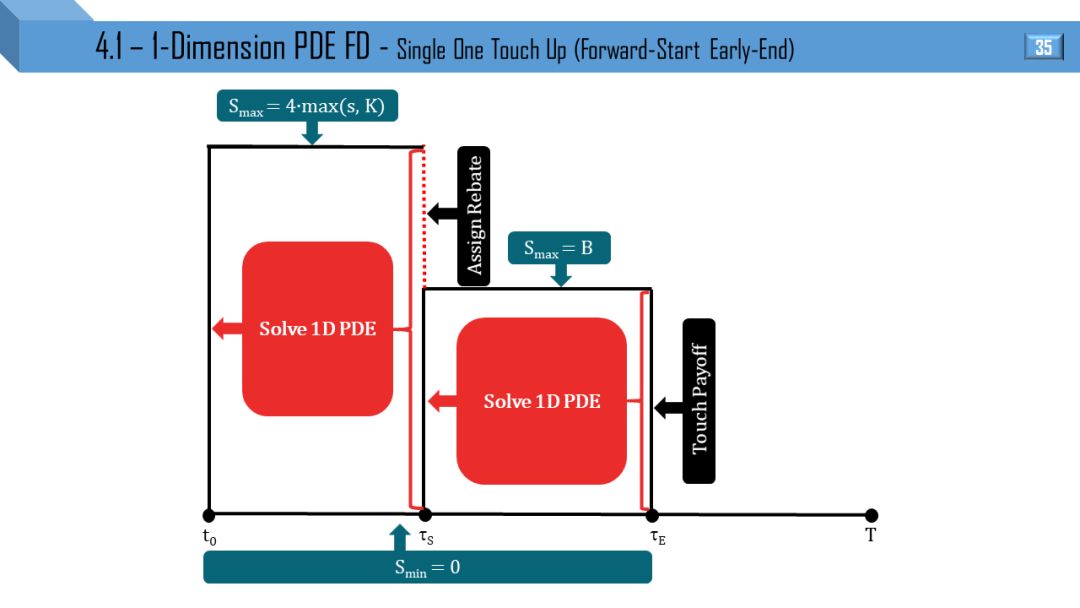
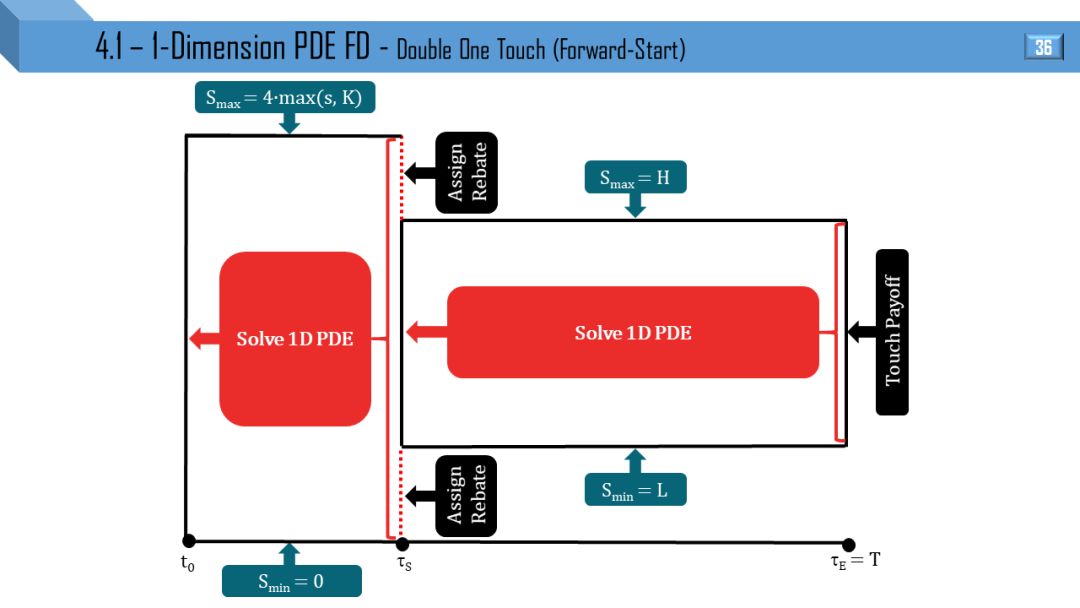
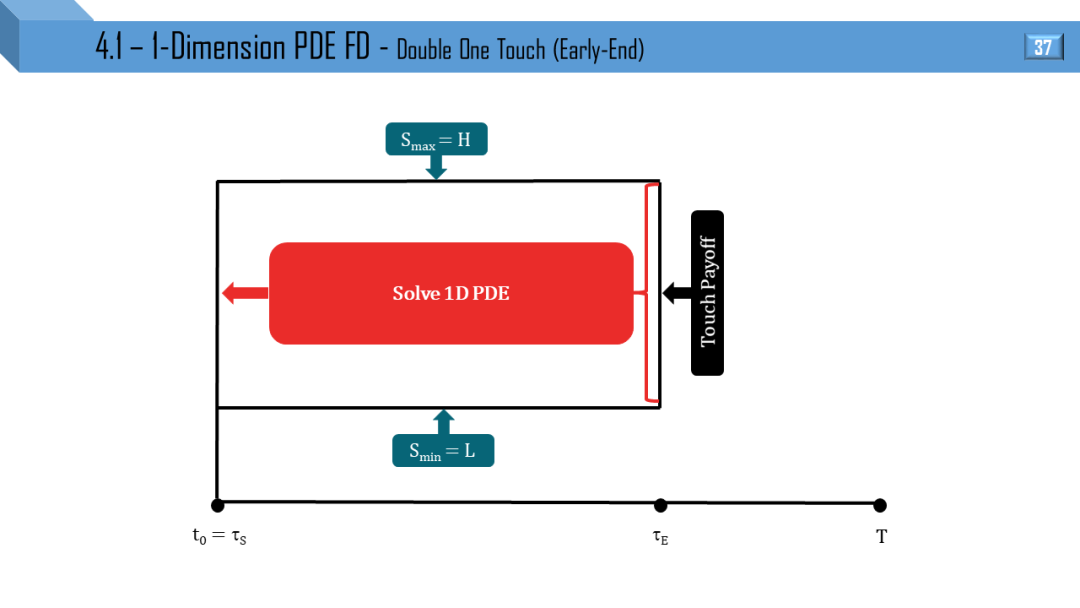
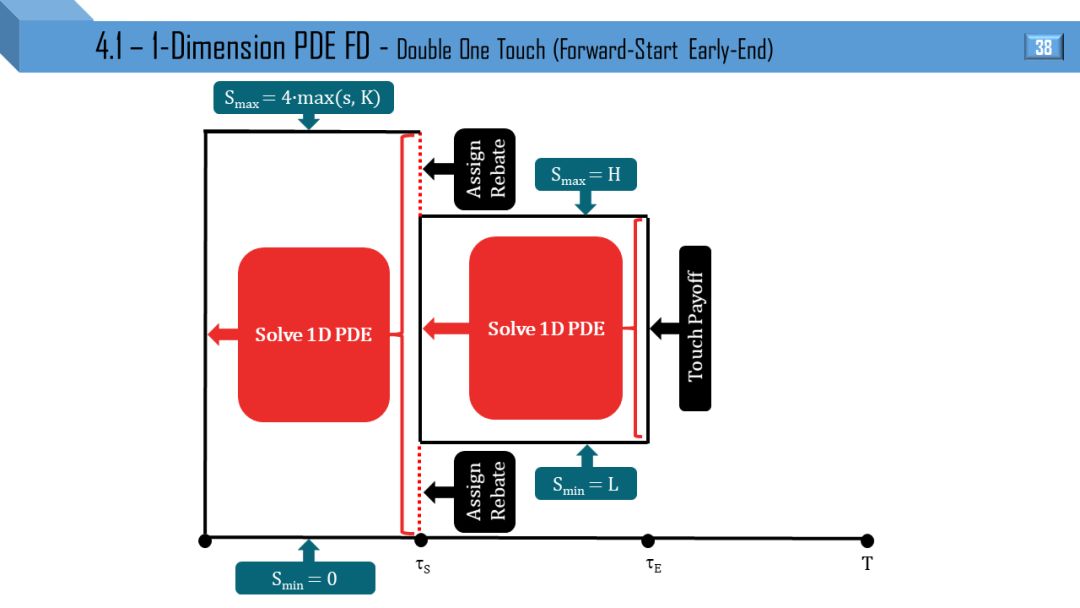
BS 和 Dupire 模型都可推出一维 PDE,两者区别就是波动率于 t 和 (S,t) 相关。后面 12 张图分别画出不同类别的障碍和触碰部分窗期权的 PDE 流程:
单障碍向上敲出
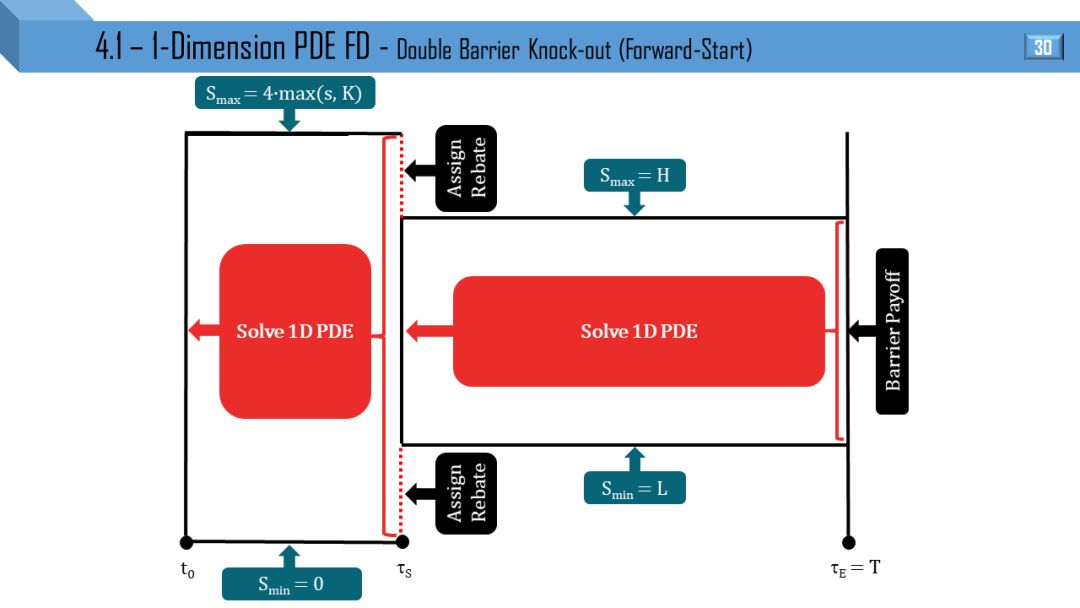
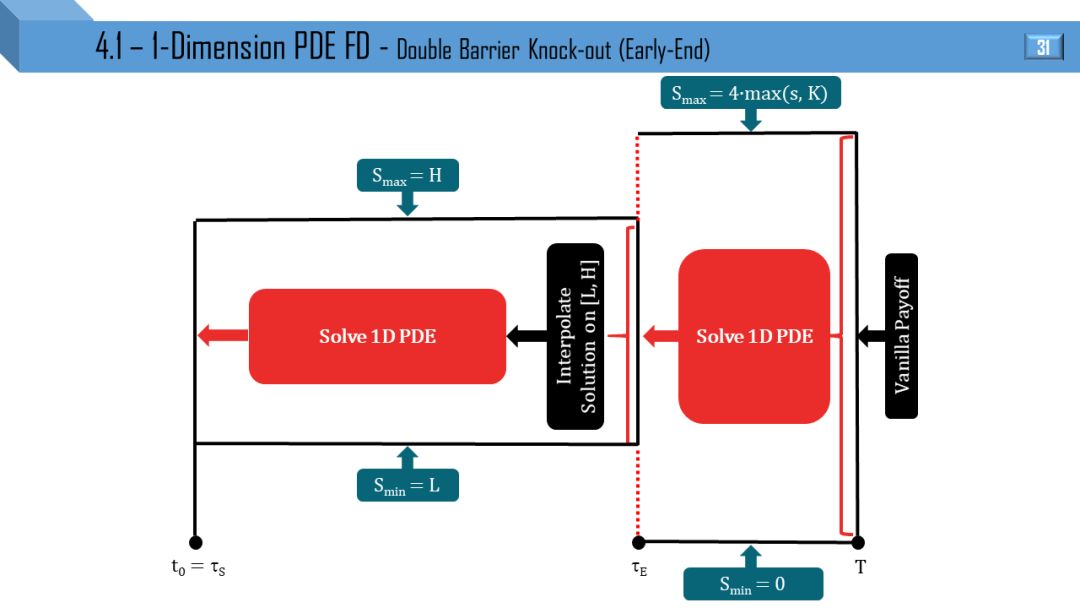
双障碍敲出
单向上触碰
双触碰
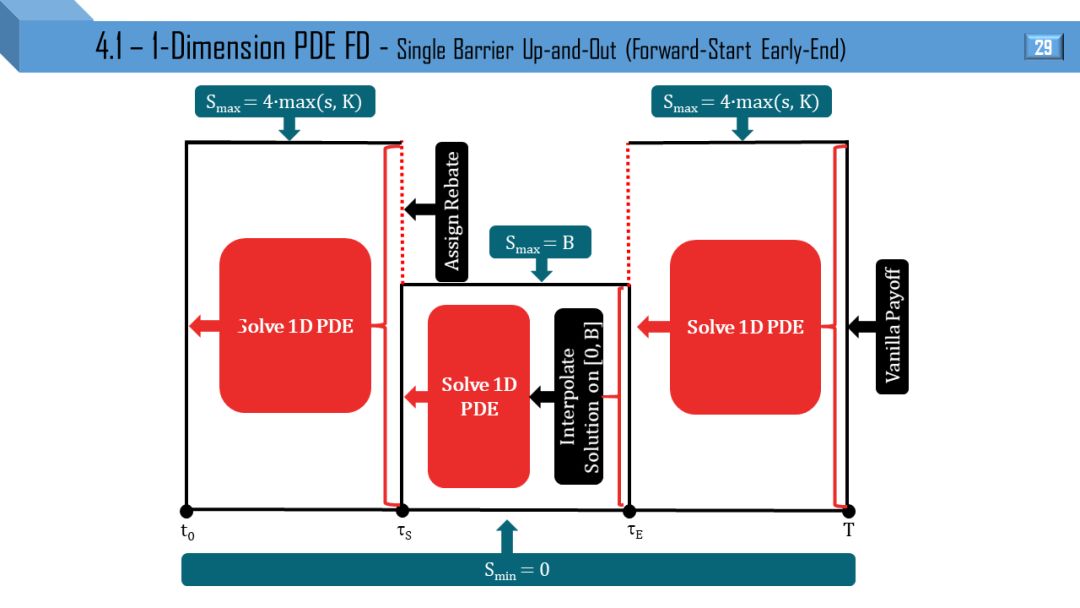
部分窗考虑到 “远期开始”,“提早终止” 和 “远期开始提早终止”。
我觉得不需要解释,看懂 1 张图就能很快类比出剩下 11 张图。建议先能懂单障碍和单触碰的流程,双障碍和双触碰可以秒懂。
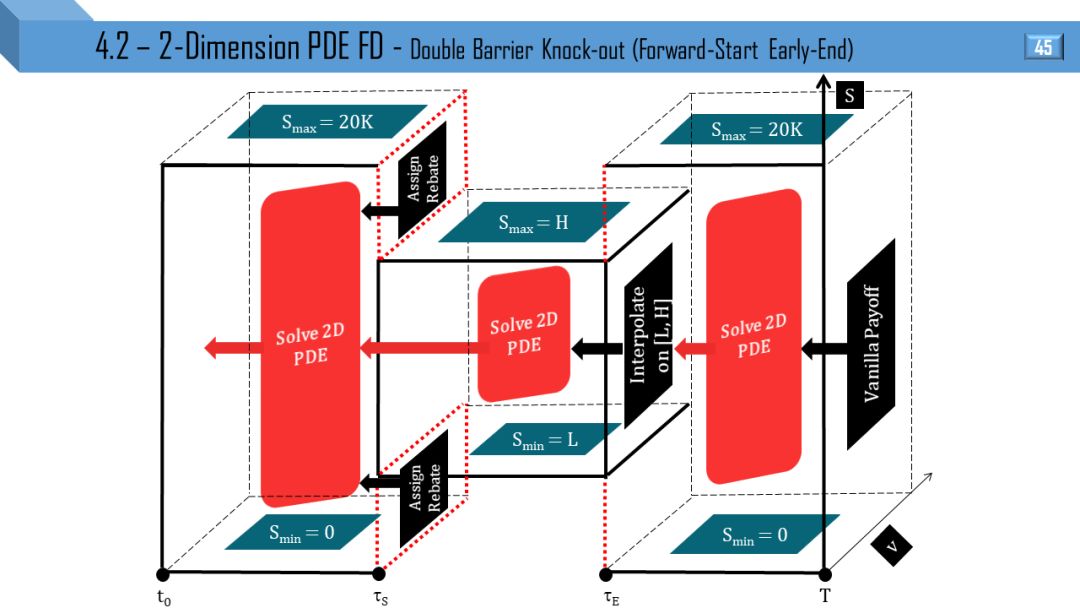
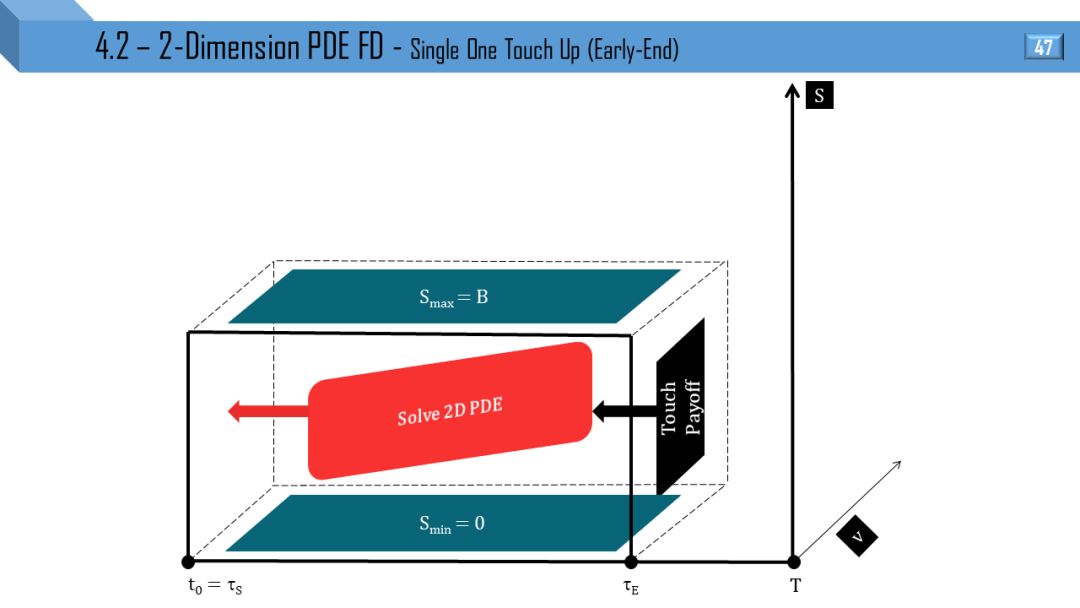
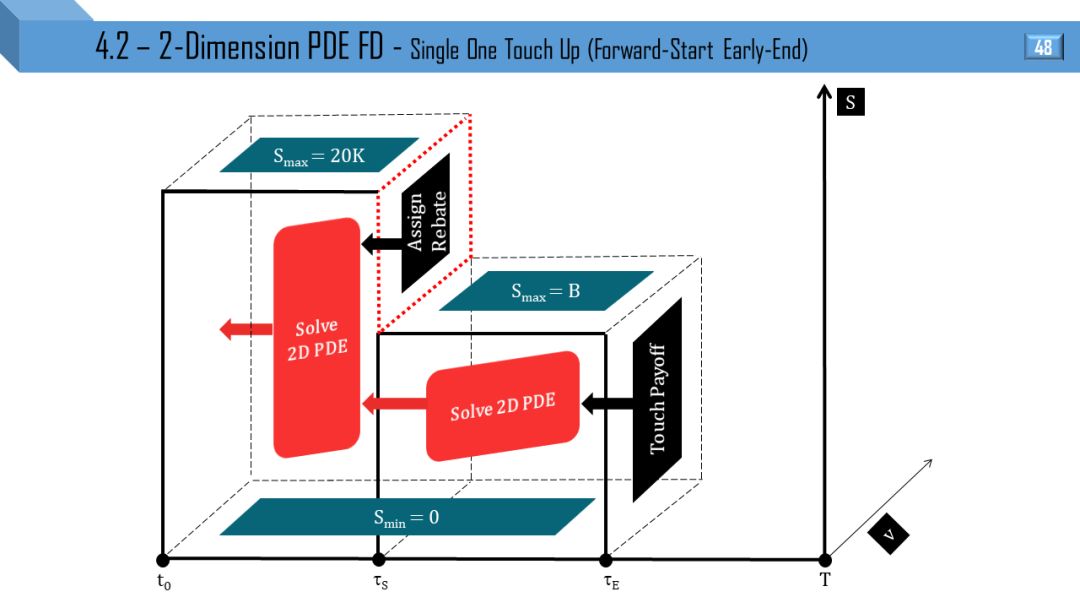
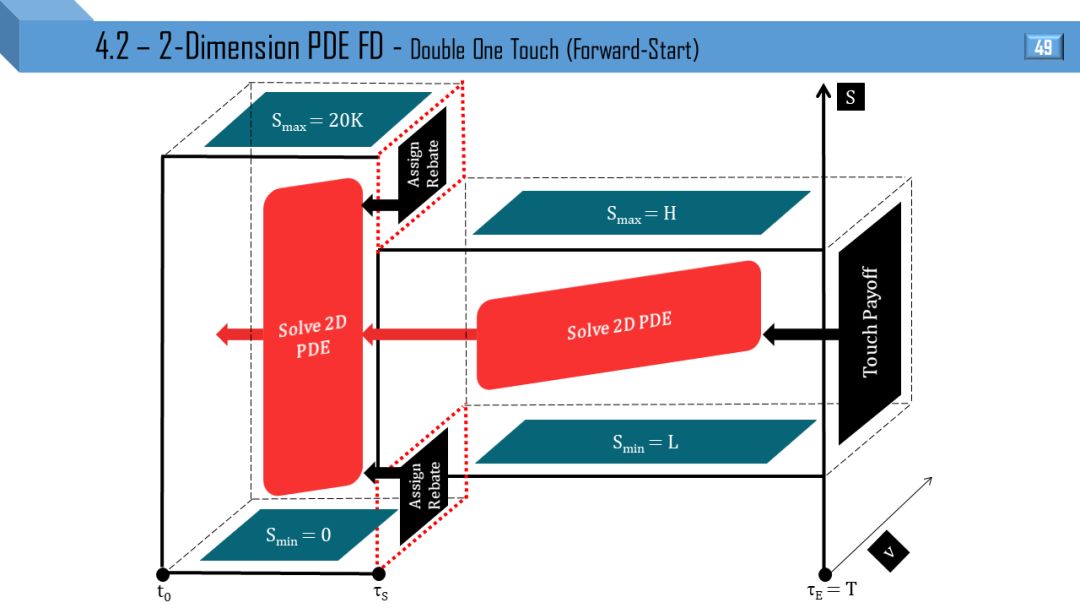
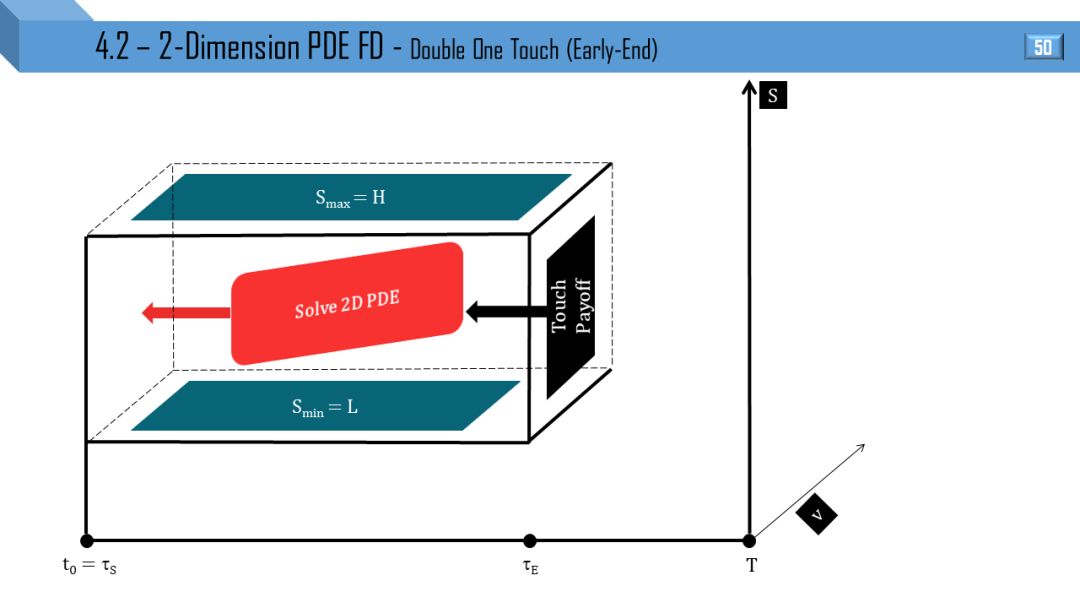
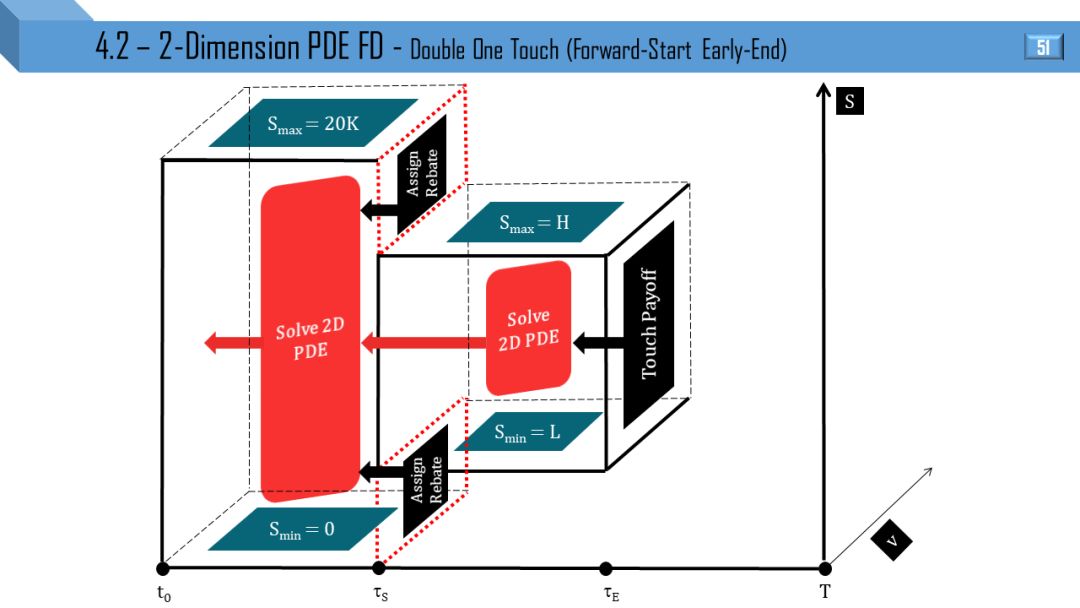
4.2
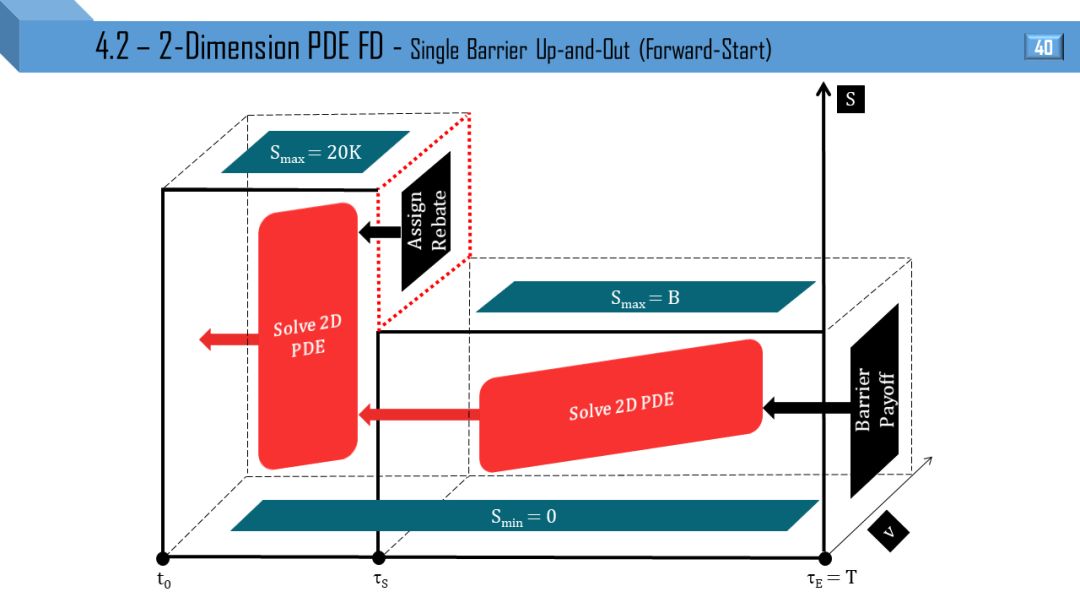
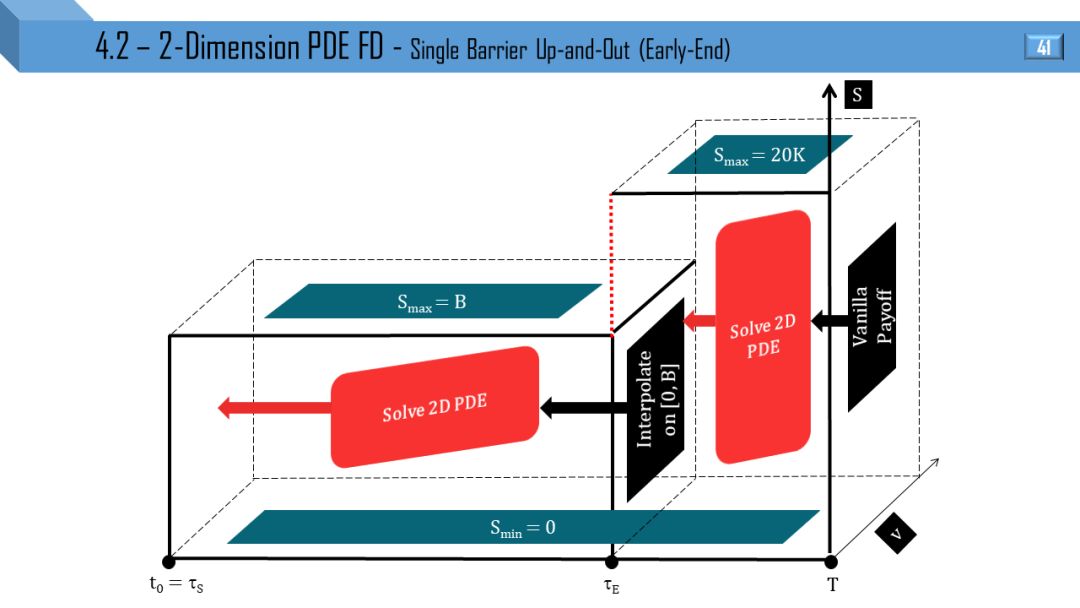
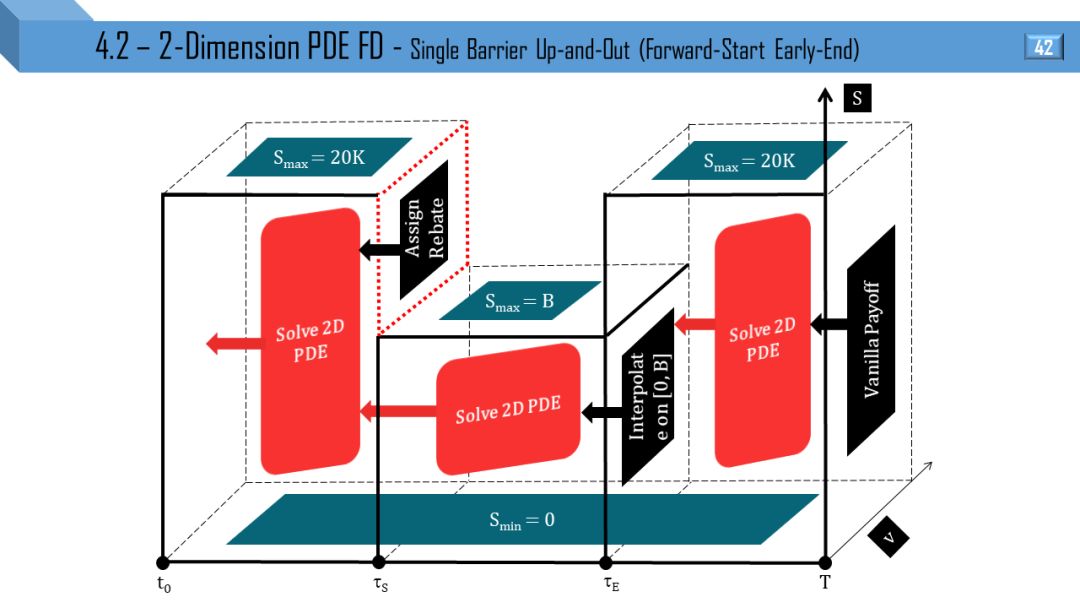
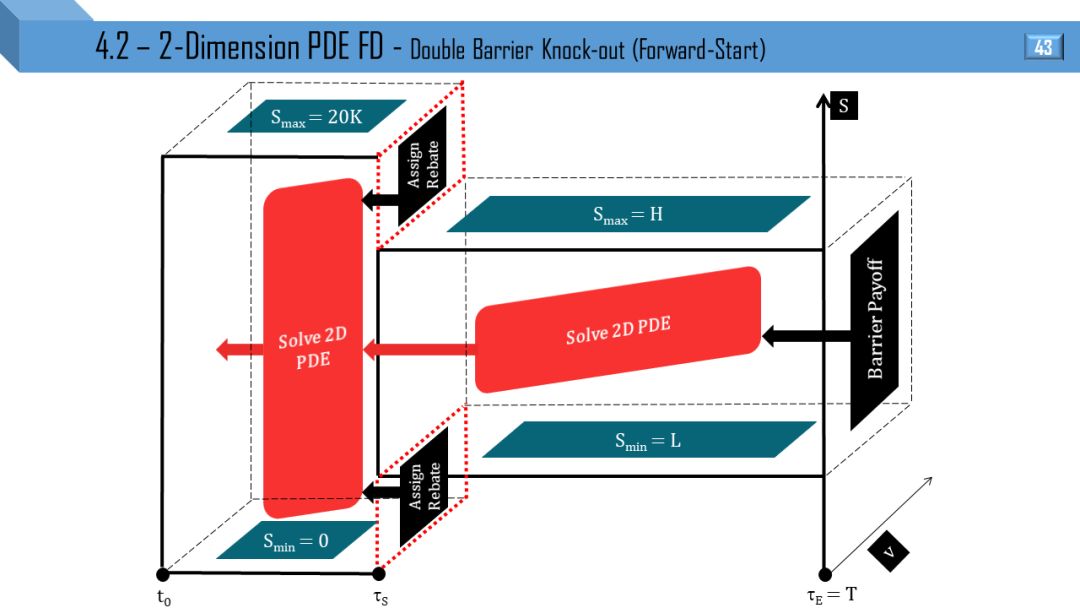
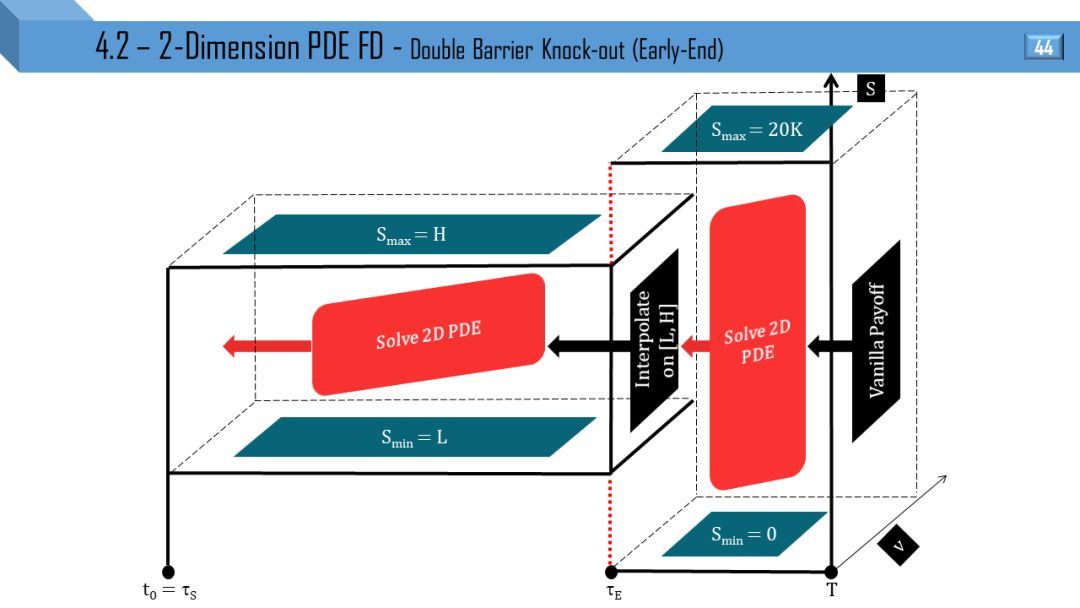
二维模型 - 偏微分方程有限差分
Heston 和 Tremor 模型都可推出二维 PDE,后者比前者多了局部波动率项。接下来 12 张图就是上节 12 张图的立体形式,所有线变成了面。
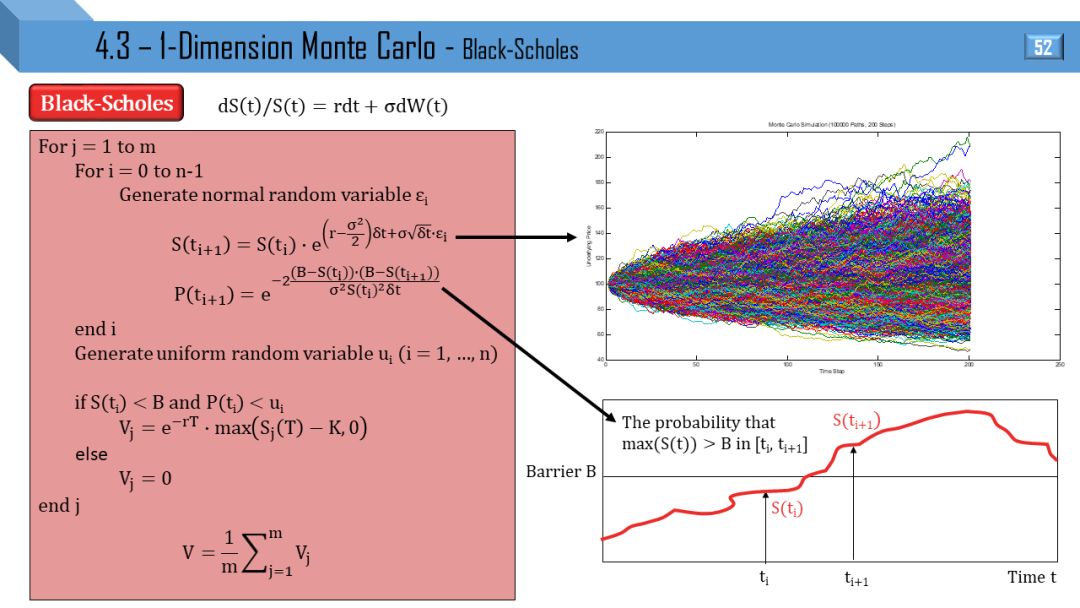
4.3
蒙特卡洛
BS 模型对应着一维蒙特卡洛方法。模拟出不同路径不同时点的原生资产价格很简单,值得一提是一个 trick,即计算 P(ti+1)。它代表着 S(t) 在 [ti,ti+1] 之间的最大值超过“上障碍 B” 的概率。
因为在 ti 和 ti+1 之间 S 还是有可能触碰障碍的,这样做导致模拟更少的路径来计算障碍期权价格,提高了效率。
Heston 模型对应着二维蒙特卡洛方法:
简单的 Euler 方案:波动率 v(t) 会生成负值,一旦发现用 0 替代,效率不高。
先进的 QE 方案:V(T) | v(t) 服从卡方分布,用一个正态变量 z 的二次幂函数近似。
QE 方案的原理比较复杂,有兴趣的同学可以参考上图里面 Leif Andersen 的论文。笔者试过,效率确实比 Euler 高到不知哪里去了,用过的都说好 :)。
总结:
障碍期权比同等欧式期权便宜,也是很多交易策略的基本组成部分。
障碍期权可以按障碍个数、障碍方向、敲入敲出特征、看涨看跌类别、窗口类型来分类。
解析解最高效,但很多时候推导非常麻烦 (双障碍部分窗) 甚至不可行 (LSV 模型)。
偏微分方程有限差分对于障碍和触碰期权最好,终止条件和边界条件非常好设置,基本上不费力可以解决所有类型的障碍和触碰期权定价问题。
蒙特卡洛最普适,通常在没有头绪时可先尝试。此外只有它适合带有障碍的多资产期权定价,因为偏微分方程有限差分有维度诅咒 (curve of dimensionality)。
注:本次讲演没有涉及到模型校正 (大课题),即如何从市场上交易活跃的欧式期权得到模型参数 (SDE 里的参数)。