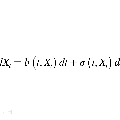随机延迟微分方程数值解的延迟依赖稳定性及自适应技术

项目名称： 随机延迟微分方程数值解的延迟依赖稳定性及自适应技术

项目编号： No.11426098

项目类型： 专项基金项目

立项/批准年度： 2015

项目学科： 数理科学和化学

项目作者： 屈小妹

作者单位： 湖北师范学院

项目金额： 3万元

中文摘要： 随机延迟微分方程广泛出现于经济学、生物、物理、电子和无线电通讯等领域，由于解析解很难直接获得，其数值解的稳定性分析具有十分重要的意义，因而受到研究人员的高度重视。本项目将研究在随机延迟微分方程解析解延迟依赖稳定性条件下，其数值解能否保持解析解的延迟依赖稳定性。与已有的研究工作相比，我们将放松延迟依赖稳定性条件，分析分步theta方法、theta-Milstein方法等数值算法在该条件下的均方指数稳定性，并对数值算例比较其精度、计算量和稳定区域。此外，我们还将针对Ito型随机延迟微分方程的弱解提出新的后验误差估计，设计实现简单并且有效的自适应欧拉方法以及Milstein方法，达到减少计算量、提高收敛速度的目的。本课题的研究是一项具有重要理论意义和实际应用价值的工作，将对现有的理论和算法有所发展。

中文关键词： 随机微分方程；延迟依赖稳定性；数值解；自适应方法；

英文摘要： Stochastic delay differential equations have been widely used in applications of economics, biology, physics, electronics, wireless communication, etc. Since analytical solution can hardly be obtained, the stability analysis of numerical methods have aroused a lot of attention.This project is to study the problem: under the delay-dependent stability conditions, whether the mean-square stablity of numerical solutions for stochastic delay differential equations can reproduce the stability of analytical solution? Compare with exist works, we shall relax the delay-dependent stability conditions, analyze the mean-square exponential stability of split-step stochastic theta methods, theta-Milstein methods, and compare with their accuracy, computation complexity and stable domain. Furthermore, we will propose new adaptive methods for stochastic delay differential equations which are easy to implement and efficient. This study is of great both theoretical and practical significance.

英文关键词： stochastic differential equation；delay-dependent stability；numerical solution；adaptive method；